Local Differential Privacy
들어가며
지난번에는 어느 한 데이터셋에서 하나의 데이터가 가지는 영향력에 대해서 공부해 보았습니다. 어떤 데이터셋에서 한 데이터를 제외한 나머지 정보를 다 알고 있을 때, 나머지 한 개의 데이터를 유출할 수 있는지에 대한 것이었습니다. Differential Privacy는 이를 수식을 활용해 표현한 것으로, $\epsilon$의 값으로 데이터의 안정성을 확인할 수 있었습니다.
이번에는 Differential Privacy와는 조금 다르지만 개인의 프라이버시를 보호할 수 있는 개념을 소개하려고 합니다. 개인이 데이터를 제공했을 때의 프라이버시를 보호하기 위한 개념인 Local Differential Privacy에 대해 소개하려고 합니다.
Local Differential Privacy (LDP)
등장 배경
기존의 DP는 데이터 셋 안에서 어느 한 데이터의 영향력을 판단하여, 노이즈를 이용해 영향력을 줄이고 그 영향력을 측정하는 것이 목적이었습니다.
그러나 이것은 결국 데이터 하나 하나에 대한 정보를 갖고 있는 것입니다. 실제로 데이터를 얻게 되는 순간, 그것이 실제의 데이터임을 알 수 있습니다.
Local Differential Privacy라고 부르는 LDP는 이것보다 한층 더 프라이버시를 신경쓰는 이론입니다.
예를 들어서, A랑 B라는 두 의견으로 나누는 경우가 있다고 생각해봅시다. A를 좋아하는 사람들이 모인 집단에서 설문조사를 했을 경우, 실제로 B를 좋아한다 하더라도 B를 좋아한다고 말할 수 없을 것입니다. 하지만 그렇다고 거짓말을 할 수 없습니다. 이 경우에, DP를 적용한다면 우리는 B를 좋아하는 사람이 있다는 사실을 알 수 있습니다.
하지만 이러한 것은 그 개인의 프라이버시를 존중하지 못하는 것이라고 볼 수 있습니다. 하지만 이런 특징을 숨기지 못한다면, 프라이버시를 보장한다고 할 수 없을 것입니다.
이를 위해서, 원래의 데이터가 가지는 특성을 최대한 지키며, 원래의 데이터를 숨기는 것이 Local Differential Privacy라고 할 수 있습니다.
이러한 식으로 데이터의 privacy를 지키는 방법으로는 randomized response가 있습니다. input perturbation라고도 하는데, 이는 원래 민감한 정보의 질문을 할 때 활용한 방법이었습니다. 설문조사의 결과를 일정 확률로 틀린 결과로 바꿔서 전달한다면, 정보를 수집하는 입장에서는 개인의 민감한 결과를 알 수 없게 됩니다.
예를 들어, B를 선택한 하나의 데이터를 A를 선택한 데이터 2개, B를 선택한 데이터 4개로 확장한다면 B가 더 많다는 것은 변함이 없지만, A를 좋아하는 그룹에서 “B를 선택한 사람이 한명은 존재한다!”라는 결과는 도출할 수 없게 됩니다.
이것과 같이, 데이터들의 특성들을 유지하면서도 데이터셋에서 그 데이터셋의 특성을 얻을 수 없도록 하는 것을 Local Differential Privacy 라고 합니다.
$\epsilon-DP$, 그리고 $(\epsilon,\delta)-DP$
지난번에 적었던 내용이지만, Database의 프라이버시 정도를 측정하기 위한 방법으로 $(\epsilon,\delta)-DP$ 가 제안되었습니다. 그래서 $(\epsilon,\delta)$-Differential Privacy 의 내용을 간단하게 다시 적어보려 합니다.
데이터셋 $D_1$이 있습니다. 그리고 $D_1$과 하나의 데이터를 제외한 나머지 데이터가 전부 같은 데이터셋 $D_2$가 있습니다.
그리고 데이터셋을 입력으로 가지는 알고리즘 $A$라고 가정합니다.
해당 조건하에서, 다음 식을 만족하는 만족하는 경우, $D_1$을 $\epsilon$-differential privacy라고 합니다.
\[Pr[A(D_1) \in S] \leq e^\epsilon \times Pr[A(D_2) \in S]\]이 식에서, $\delta$항을 추가한다면 $(\epsilon, \delta)$-differential privacy 라고 합니다.
\[Pr[A(D_1) \in S] \leq e^\epsilon \times Pr[A(D_2) \in S] + \delta\]제안된 이 방법에서 얻는 $\epsilon, \delta$ 값을 통해 프라이버시의 정도를 측정하고, 판단할 수 있게 되었습니다.
$\epsilon$-Local Differential Privacy
$(\epsilon, \delta)$-Differential Privacy 의 정의를 한번 다시 돌아보았습니다. 하지만 Local Differential Privacy는 Differential Privacy와 다른 방법을 사용하여 비교합니다.
Local Differential Privacy는 Differential Privacy와 다르게 어떤 데이터를 특정지을 수 없게 하는 것이기 때문에, 일반적인 두 데이터를 통해 비교합니다. $\epsilon$-Local Differential Privacy의 정의를 보면 다음과 같습니다.
어떤 두 데이터 $x, x’$과 랜덤한 알고리즘 A가 있다고 생각합시다.
다음의 식을 만족하면 알고리즘 A가 $\epsilon$-Local Differential Privacy 를 만족한다고 합니다.
\[Pr[A(x) \in S] \leq e^\epsilon \times Pr[A(x') \in S]\]간단하게 하면 데이터를 input으로 받아 결과물을 내는 알고리즘 A가 있다고 했을 떄, 두 데이터가 같은 결과물 안에 속할 확률이 $e^\epsilon$ 인 경우, $\epsilon$-LDP 를 만족한다고 합니다.
해당 Local Differntial Privacy를 위한 알고리즘으로, RAPPOR에 대해 소개하려 합니다.
RAPPOR - Randomized Aggregatable Privacy-Preserving Ordinal Response
개요
이 논문은 Local Differential Privacy를 소개하면서, 이 개념이 적용된 예시를 위해 소개합니다. 이 논문은 Google이 Chrome 홈페이지에 대한 정보나 다른 프로세스에 대한 정보들을 수집할 때 사용된 Local Differential Privacy의 적용 방법입니다.
RAPPOR은 데이터를 수집하는 과정에서 numeric value 하나에 어떠한 방식으로 Local Differential Privacy를 적용하는지 제안하고 설명하고 있습니다.
RAPPOR이란?
RAPPOR이란 Randomized Aggregatable Privacy-Preserving Ordinal Response의 줄임말로, 구글에서 사람들의 정보들을 수집하기 위해서 구글에서 제안한 randomized response입니다. 이 방법은 randomzied response 중에서도 여러 데이터 중에 하나를 고르는 정답에 대해서 Local Differential Privacy를 제공합니다.
RAPPOR 알고리즘
RAPPOR의 과정을 알아보겠습니다. 먼저, 알고리즘을 보면 다음과 같은 과정입니다.

RAPPOR은 먼저 어느 한 값의 데이터를 받으면, 해쉬함수 h와 정해진 사이즈 k를 통해 Bloom Filter B를 제작합니다.
제작된 Bloom Filter B의 각 비트 $B_i$를 활용하여 Fake Bloom Filter를 제작합니다. Fake Bloom Filter를 제작하기 위해 특정 확률 $f$를 사용합니다. $B’_i$ 는 $1-f$의 확률로 각 Bloom Filter의 $B_i$들을 그대로 보존합니다. 그리고 나머지 $f/2$, $f/2$의 확률로 0과 1을 무작위로 정해서 Fake Bloom filter $B’$을 제작합니다.
마지막으로 Fake Bloom Filter를 통해 제작된 데이터에서 $B’_i$이 0일때랑 1일때, 각각 p와 q의 확률로 서버에 제출할 마지막 데이터 $S_i$의 값을 1로 정합니다. 이렇게 만든 S를 서버에 제출합니다.
예시를 들면, 다음의 사진과 같습니다.
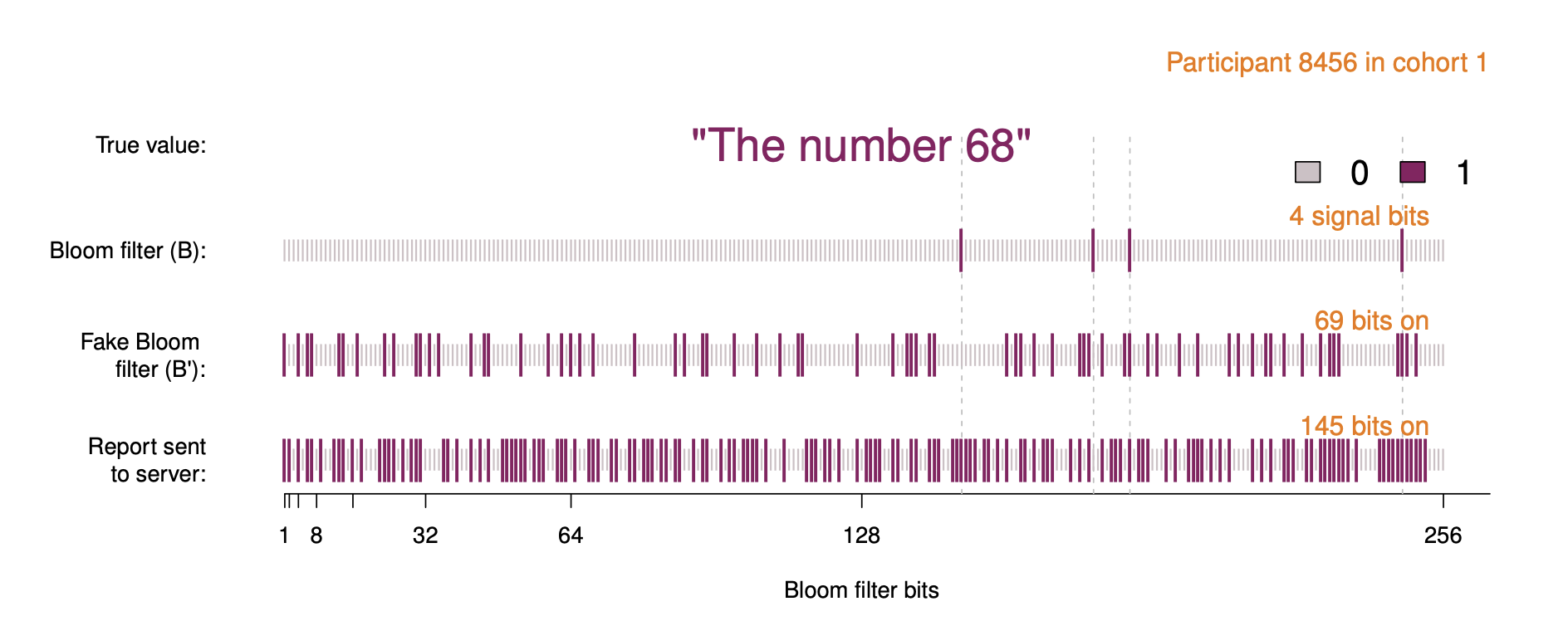
실제로 Local Differential Privacy를 위한 과정은 이게 전부입니다. 각 과정별로 큰 알고리즘도 없기 때문에 연산량도 적고, Client의 기기에서 빠르게 수행이 가능합니다. Local Differential Privacy가 적용되어 있으면서 정해진 확률 $f, p, q$를 통해 randomize하고있기 때문에 2중으로 보호하고 있습니다.
Differential Privacy of RAPPOR
이번에는 처음에 다루었던 $\epsilon$-Local Differential Privacy을 통해 RAPPOR의 privacy를 측정하려고 합니다.
실제로 어떤 input $v$를 넣었을 때 $S$ 라는 결과가 나오는 경우를 생각해보겠습니다. 이 경우가 일어날 확률을 각 단계별로 식으로 세워보면 다음과 같습니다.
\[\begin{aligned} P(S=s|V=v) &= P(S=s|B,B',v) \cdot P(B'|B,v) \cdot P(B|v) \\ &= P(S=s | B') \cdot P(B'|B) \cdot P(B|v) \\ &= P(S=s | B') \cdot P(B'|B) \end{aligned}\]그리고 이 과정에서, $P(B’|B)$ 는 실제 $b_i, b’_i$의 값과 $f$를 통해서 예측할 수 있습니다. 이를 식으로 써보면, 다음과 같습니다.
\[\begin{aligned} P(b'_i=1 | b_i=1) &= {1 \over 2} f +1 - f = 1 - {1 \over 2} f \\ P(b'_i = 1 | b_i = 0) &= {1 \over 2}f \\ \end{aligned}\]이를 이용해서, $ P(B’=b’ | B=b ^ \star ) $ 일 확률을 계산해보면 다음과 같습니다. 편한 계산을 위해, 일관성을 잃지 않고 $B’$에서 $b’_1$ ~ $b’_h$이 1이고, 나머지는 0이라고 가정하겠습니다.
\[P(B' = b' | B = b^ \star) = \overset{h}{\underset{i=0}{\prod}} ({1 \over 2} f) ^ {b'_i} (1-{1 \over 2}f) ^ {1-b_i'} \times \overset{k}{\underset{i=h+1}{\prod}} (1 - {1 \over 2} f) ^ {b'_i} ({1 \over 2}f) ^ {1-b_i'}\]이러한 값을 얻고, 두 input에 대해 다음 식으로 $\epsilon$의 계산이 가능합니다.
\[ln {Pr[A(x) \in S] \over Pr[A(x') \in S]} \leq \epsilon\]위 식에 그대로 대입하고 난 뒤 최댓값을 구한다면, $b’_i$들이 같은 값일수록 큰 값이 나옴을 알 수 있습니다. 즉, 제일 작게 계산이 될 경우는 $\epsilon$값이 다음과 같이 유도됩니다.
\[\epsilon \leq ln({ { 1- {1 \over 2}f} \over {1 \over 2}f })\]비슷하게 Server에 Report하기 마지막 전 단계에 대한 $\epsilon$도 동일한 방법으로 계산이 가능하며, 계산시 다음과 같은 $\epsilon_1$을 얻을 수 있습니다.
\[\epsilon_1 = h \cdot log ({q^\star (1-p^\star) \over {p^\star (1-q^\star)}})\]이와 같이 Local Differential Privacy를 적용할 수 있고, RAPPOR에서 정의한 확률에 따라 $\epsilon$값이 달라짐을 알 수 있습니다.
결론
이번에는 Local Differential Privacy의 개념과, 현재 어떠한 방식으로 사용되는지 Google이 제안한 RAPPOR를 통해 확인해볼 수 있었습니다. Local Differential Privacy가 적용되는 것은 굉장히 특정한 상황일 수 있으나, 실제로 Differential Privacy를 활용하는 것보다는 조금 더 높은 프라이버시를 보장할 수 있을 것입니다. 이는 분산학습을 하는 경우에, 각 Client들의 데이터를 모으는 과정에서 사용되는 등, 여러 확장 가능성이 있음을 알 수 있었습니다.