Sequence model: from RNN to Attention
Introduction
Sequence model은 연속적인 데이터를 입력으로 받아서 연속적인 데이터를 출력하는 모델을 의미합니다. 다시 말해, 시계열 데이터를 다루는 모델이라고 할 수 있습니다. Sequence model이 사용되는 대표적인 task로는 번역, 챗봇, 동영상 생성 등등이 있습니다. 이번 글에서는 가장 기초적인 Sequence model인 RNN부터 요즘 모든 딥러닝 분야에서 필수적으로 사용되는 개념인 Attention까지 발전 흐름을 따라 알아보고자 합니다.
RNN
overview
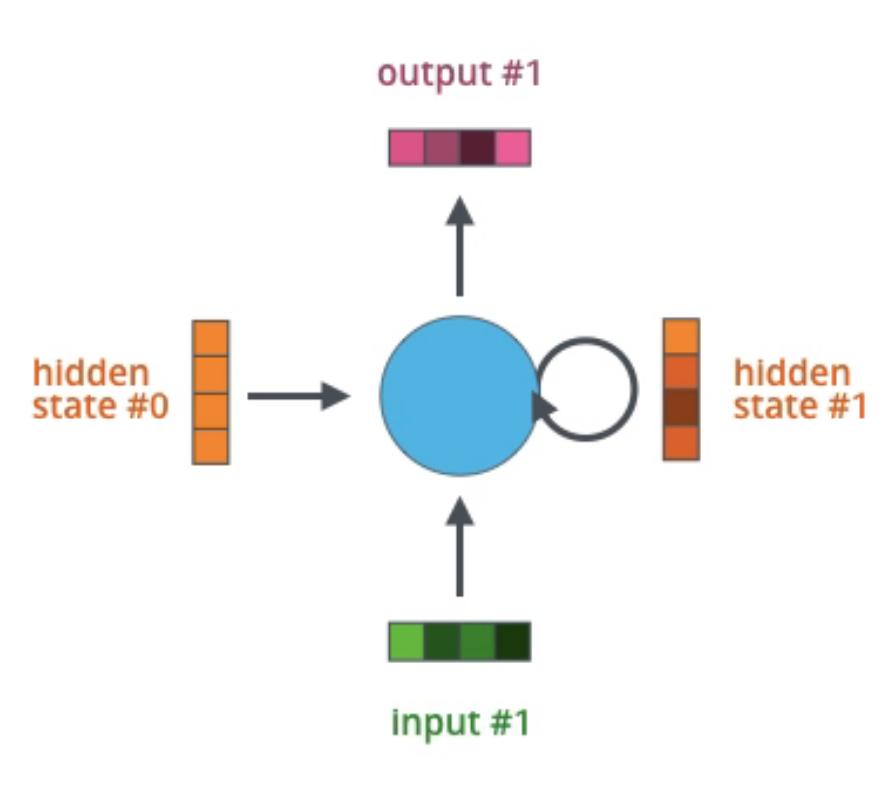
RNN (Recurrent Neural Network)은 서로 독립적인 데이터가 아닌 연속적인 데이터를 다루기 위한 신경망입니다. 연속적인 데이터를 시계열 데이터라고도 하는데, 주가, 음성, 대화, 글, 동영상 등과 같이 일정 시간 간격으로 배치된 데이터라소 보시면 됩니다. RNN은 가장 초기에 나온 신경망인 만큼 시퀀스 데이터를 다루는 기술의 근간이라고 할 수 있습니다. RNN은 데이터 간의 상관관계를 학습하기 위해 Recurrent(→cycle) 구조를 활용합니다. 이 구조를 이용해서 네트워크 내부에 상태를 유지 및 기억합니다. 즉, 이전 단계에서 계산된 정보를 가공하여 다음 단계의 계산에 반영하게 됩니다.
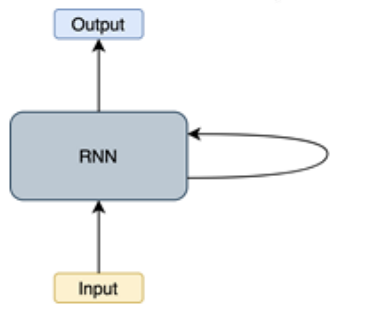
RNN
표현방법
자세한 설명에 앞서, RNN을 표현하는 2가지 방법에 대해 소개하겠습니다. time-unfolded와 time-folded가 그것들입니다. time-unfolded는 말 그대로 각 시간에 대해서 네트워크를 여러 번 표시한 것이고, time-folded는 시간에 관계없이 존재하는 네트워크를 표현하는 방식입니다. 이러한 표현방법은 RNN에만 적용되는 것이 아니라 Sequence model에 모두 사용될 수 있습니다. time-unfolded에서 여러 개의 네트워크가 표시된다고 하더라도 실제로 여러 네트워크가 존재하는 것이 아니라는 점을 꼭 유의하시길 바랍니다. 아래 그림을 참고하시면 이해에 도움이 될 것입니다. h는 하나의 hidden layer를 의미하고 T는 sequence data의 길이입니다.
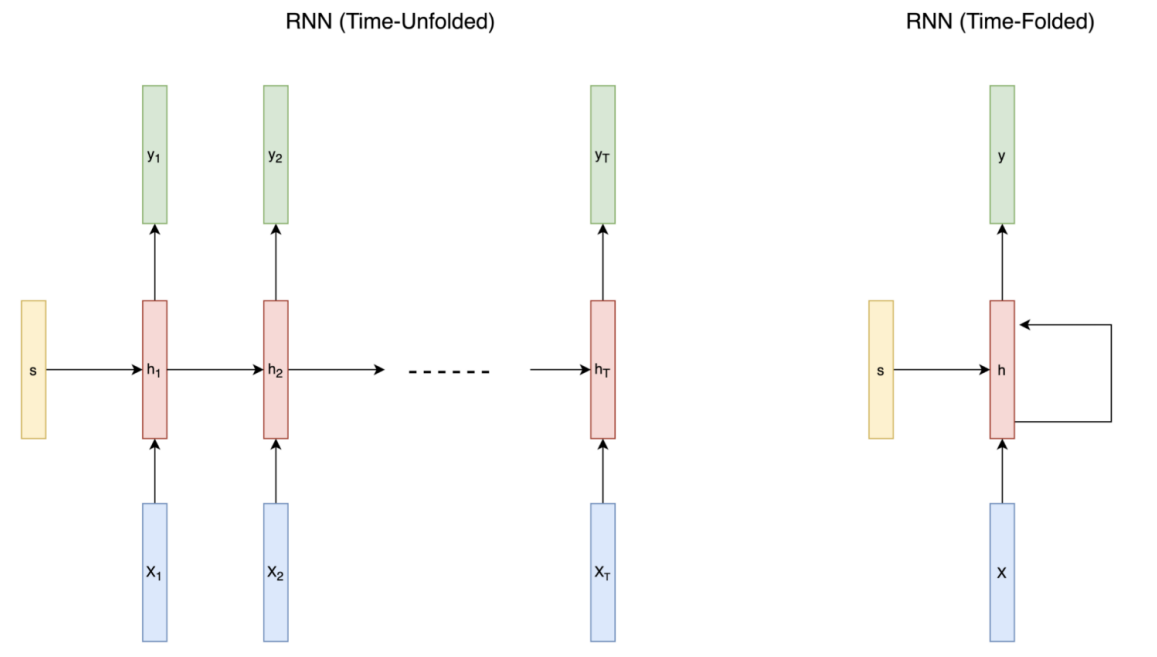
time-unfolded와 time-folded
RNN의 발전
RNN은 1986년에 나온 개념으로 지금까지 상당히 많은 형태로 발전되어 왔습니다. 주로 모델이 학습이 잘 되지 않는 문제점을 해결하는 방향으로 발전되었습니다.
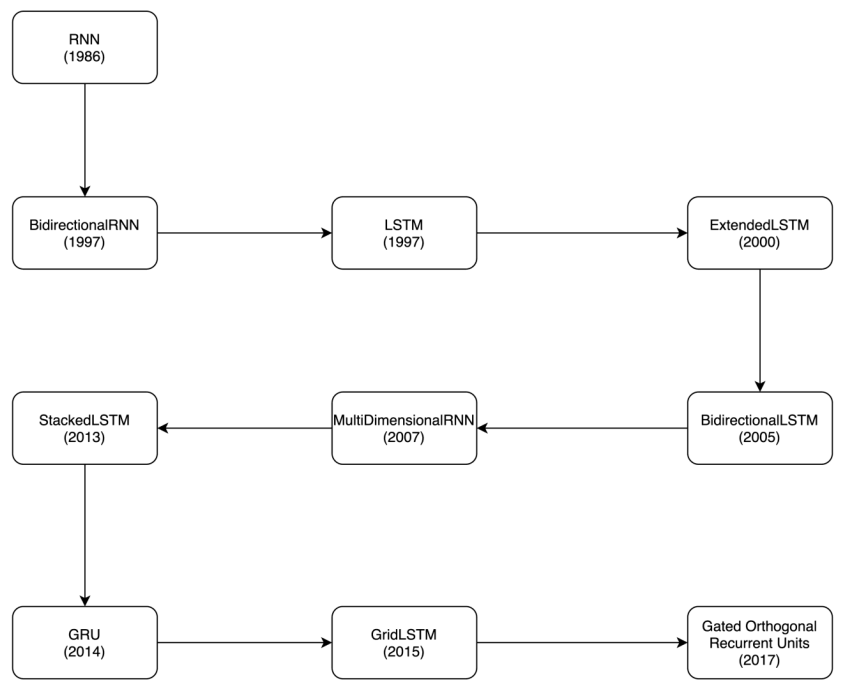
RNN의 발전
입출력에 따른 RNN의 종류
입출력 데이터의 형태에 따라서 RNN을 4가지 종류로 구분할 수 있습니다.
-
many to one
여러 input을 받아서 하나의 output을 출력하는 RNN입니다. 예를 들어 감정을 분석하는 task가 이에 해당합니다. 연속된 단어의 집합인 문장이라는 input 데이터가 주어지면 긍정, 부정, 중립 등 하나의 output을 출력합니다.
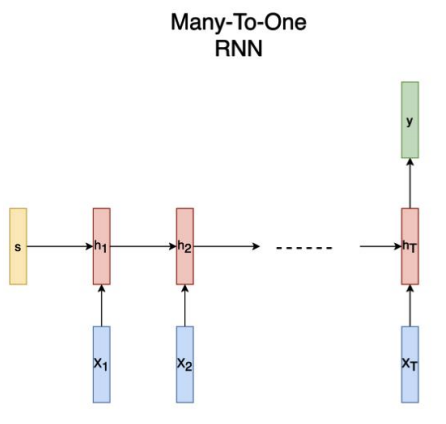
many to one
-
one to many
하나의 input을 받아서 순차적으로 여러 output을 출력하는 RNN입니다. 예를 들어 이미지 캡션을 생성하는 task가 이에 해당합니다. 하나의 이미지가 input으로 주어지면 이를 설명하는 연속적인 단어, 즉 문장을 output으로 출력합니다.
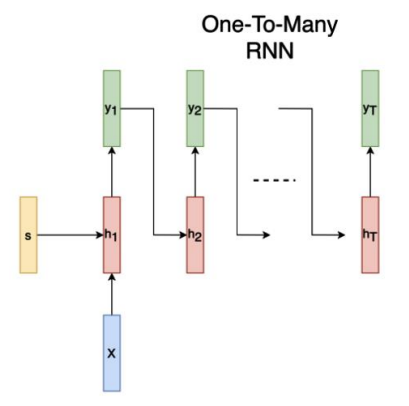
one to many
-
many to many (Instantaneous)
여러 input을 받아서 순차적으로 여러 output을 출력하는 RNN 중 하나입니다. 예를 들어 개체 인식 task가 이에 해당합니다. 연속적인 단어의 집합인 문장이 input으로 주어지면 이름, 조직, 위치 등과 같은 여러 개의 output을 출력합니다.
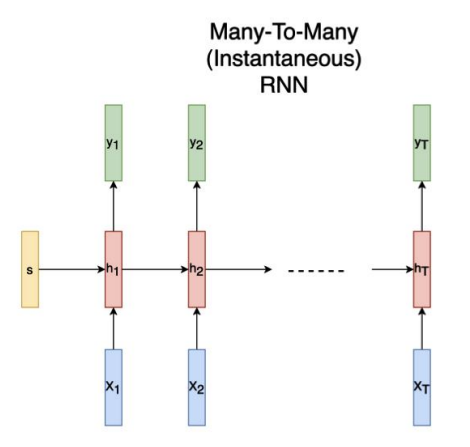
many to many (Instantaneous)
-
many to many (encoder-decoder)
마찬가지로 여러 input을 받아서 한번에 여러 output을 출력하는 RNN 중 하나입니다. 예를 들어 번역 task가 이에 해당합니다. 연속적인 단어의 집합인 문장이 input으로 주어지면 이를 다른 언어로 변역하여 연속적인 단어의 집합인 문장을 output으로 출력합니다.
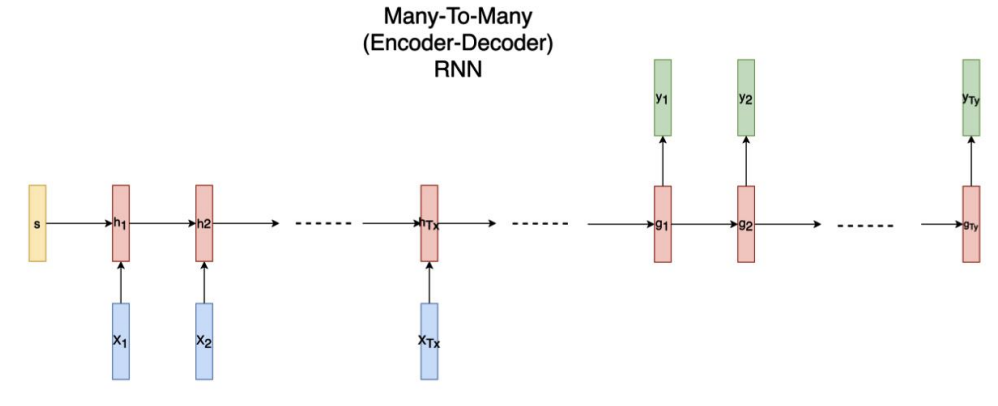
many to many (encoder-decoder)
RNN 내부 구조
RNN의 내부 구조를 살펴보면 아래와 같습니다. RNN의 hidden layer는 t시점에서 $x_t$를 input으로 받아서 linear 연산을 수행한 후, activation 함수의 input으로 넣습니다. 아래 그림에서는 tanh 함수가 activation 함수로 사용된 모습입니다. 여러 hidden layer를 거친 후, 마지막으로 다시 linear 연산을 거쳐서 t시점의 output $y_t$를 출력하게 됩니다.
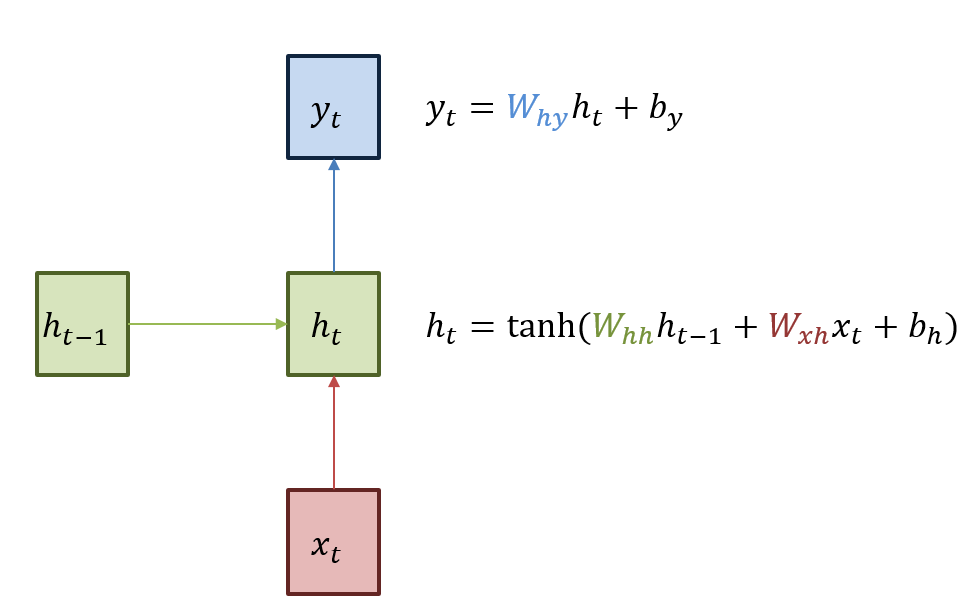
RNN 내부 구조
Gradient Vanishing, Gradient Exploding
앞서 살펴본 t 시점의 hidden layer의 output인 $h_t$를 계산하는 식을 자세히 살펴보겠습니다.
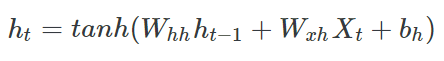
RNN 학습시 back propagation을 위해 각 시점에서 $h_t$를 미분하게 됩니다. 그 과정은 아래와 같습니다.
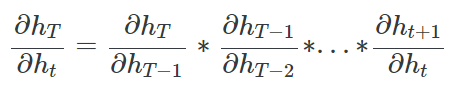
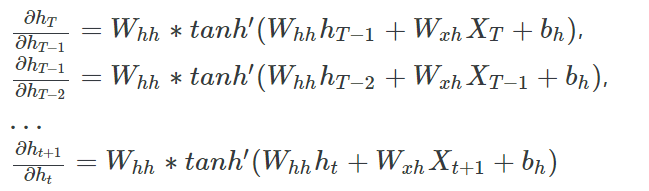
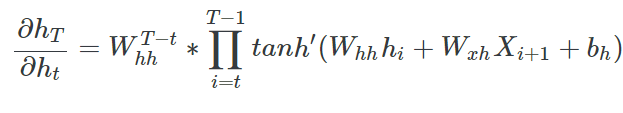
위 식을 보면 미분값에 $W^{T-t}_{hh}$가 포함되어 있는데 시계열이 길다면, 즉 $T-t$가 큰 경우에는 W 값에 따라서 Gradient Vanishing, Gradient Exploding이 필연적으로 발생하게 됩니다. W 값이 작다면 미분값이 굉장히 작아져서 Gradient Vanishing 문제가 발생하게 될 것이고, W 값이 크다면 미분값이 굉장히 커져서 Gradient Exploding 문제가 발생하게 될 것입니다. 이를 통해 RNN은 구조가 간단하지만 학습을 제대로 시키기에 힘들다는 것을 유추할 수 있습니다.
tanh 함수를 사용하는 이유
이 문제점을 최대한 완화하기 위해서 RNN에서는 activation 함수로 주로 tanh 함수를 사용합니다.
앞서 살펴본 미분값에 activation 함수의 도함수가 시계열의 길이인 T만큼 곱해집니다. 따라서 W 값에서와 마찬가지로 activation 함수의 도함수의 값에 따라 Gradient Vanishing, Gradient Exploding 문제가 발생할 가능성이 매우 높습니다.
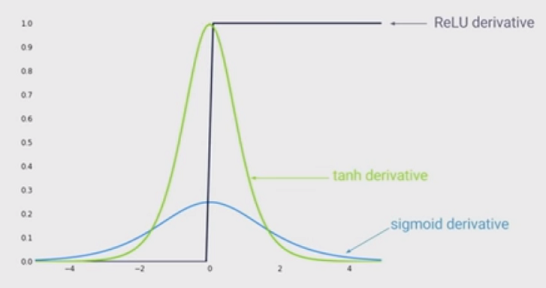
아래 그림은 3가지 activation 함수의 도함수를 나타낸 것입니다. 먼저 ReLU 함수의 도함수의 값은 0 아니면 1이기 때문에 학습이 거의 되지 않을 것입니다. sigmoid 함수의 도함수의 값은 최댓값이 0.3을 넘지 않을만큼 작기 때문에 Gradient Vanishing 문제가 발생하기 쉬울 것입니다. 따라서 그나마 tanh 함수의 도함수의 값이 0과 1사이에 분포되어 있어 Gradient Vanishing, Gradient Exploding 문제가 발생할 가능성을 낮출 수 있습니다.
RNN 구현
간단하게 pytorch를 이용해서 rnn을 구현해보겠습니다. 사용한 데이터는 2019-01-30부터 2020-10-30까지의 코스피 주가 데이터입니다. 이 데이터를 이용해서 미래 주가를 예측하는 간단한 RNN 모델을 구현해보았습니다. 데이터는 MinMaxScaler를 이용해 값을 정규화하여 사용하였습니다. 코드와 결과는 https://www.kaggle.com/code/junhyeog/rnn-kospi에서 확인하실 수 있습니다.
baseline 모델 및 학습을 위한 코드는 아래와 같습니다.
batch_size = 64
test_ratio = 0.5
sequence_length = 4
train_dataset, test_dataset, train_loader, test_loader = build_data(
x, y, batch_size, test_ratio, sequence_length
)
model = VanillaRNN(
input_size=5,
hidden_size=8,
output_size=1,
seq_len=sequence_length,
num_layers=2,
nonlinearity="tanh",
device=device,
).to(device)
criterion = nn.MSELoss()
optimizer = optim.Adam(model.parameters(), lr=1e-3)
train(model, criterion, optimizer, train_loader, num_epochs=1000)
test(model, criterion, train_dataset, test_dataset, sequence_length, batch_size)
baseline 모델의 total loss는 0.0016370388163652802 이며, 주가 예측 결과는 아래와 같습니다.
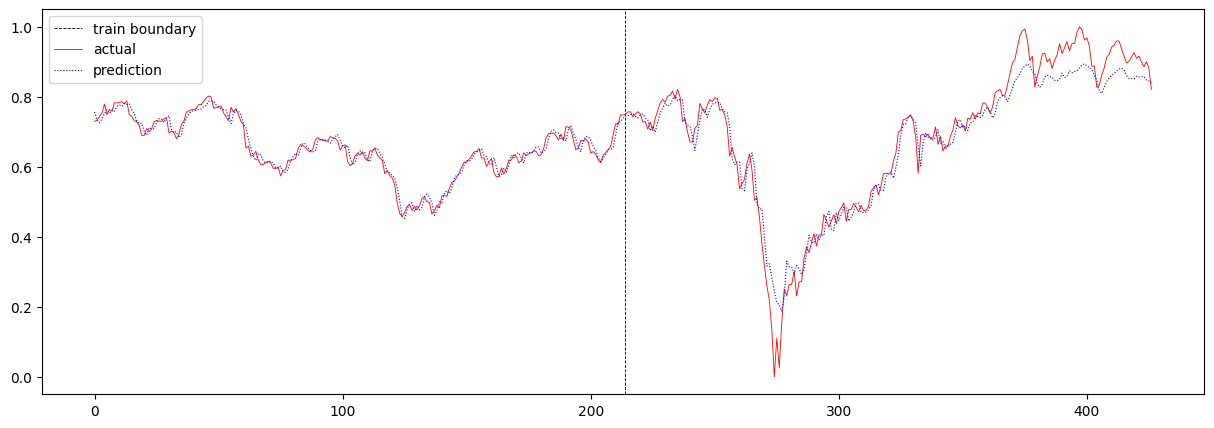
다음으로 sequence 길이를 4에서 16으로 증가시켜보았습니다. 여기서 sequence 길이란 T의 값을 의미합니다. 이 때의 total loss는 0.0036773809551959857 이며, 주가 예측 결과는 아래와 같습니다.
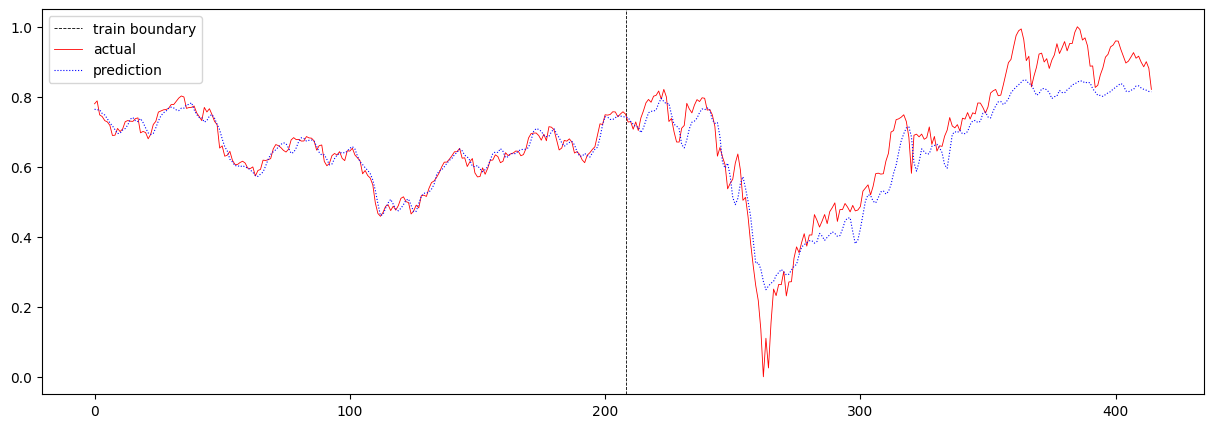
T를 증가시켰더니 loss가 증가하고 눈으로 보기에도 예측값이 실제값과 크게 다름을 확인할 수 있습니다. 여기서 알 수 있는 점은 T가 크다고 해서 학습이 잘되지는 않는다는 것입니다. 혹은 주가 예측에 있어서 이전 16일 간의 데이터를 보고 예측하는 것보다, 이전 4일 간의 데이터를 보고 예측하는 것이 더 정확하다고 해석할 수도 있습니다.
이번에는 sequence 길이를 16에서 32로 더 크게 증가시켜보았습니다. 이때의 total loss는 0.003348324296114567 이며, 주가 에측 결과는 아래와 같습니다.
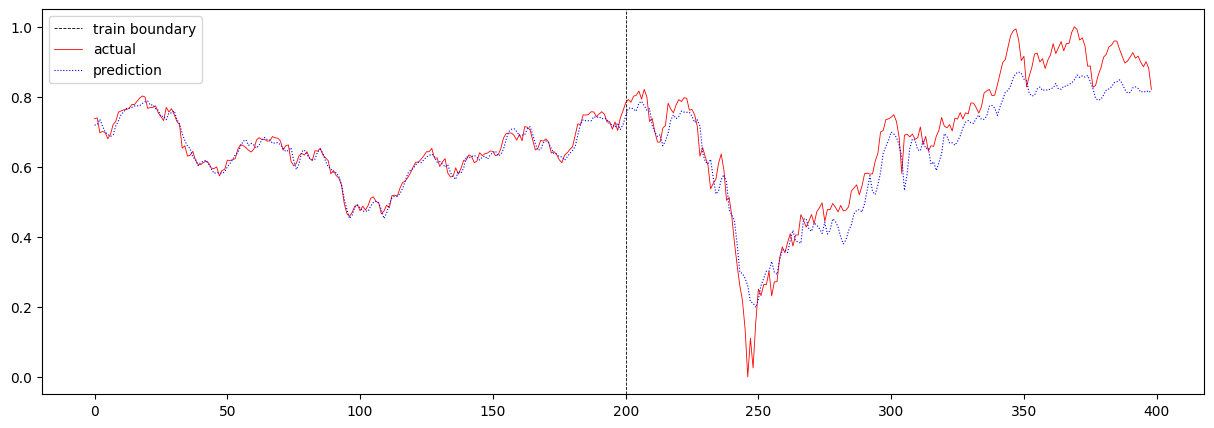
T가 16일 때와 크게 다르지 않음을 확인할 수 있습니다.
RNN의 scale이 충분하지 않아서 긴 sequence 데이터를 제대로 기억하지 못했을 수 있기 때문에, 마지막으로 T가 32인 상황에서 RNN의 scale을 증가시켜보았습니다. hidden layer의 수를 2개에서 4개로 늘렸고, hidden size를 8에서 16으로 늘렸습니다. 이때의 total loss는 0.007778501522677418 이며, 주가 예측 결과는 아래와 같습니다.
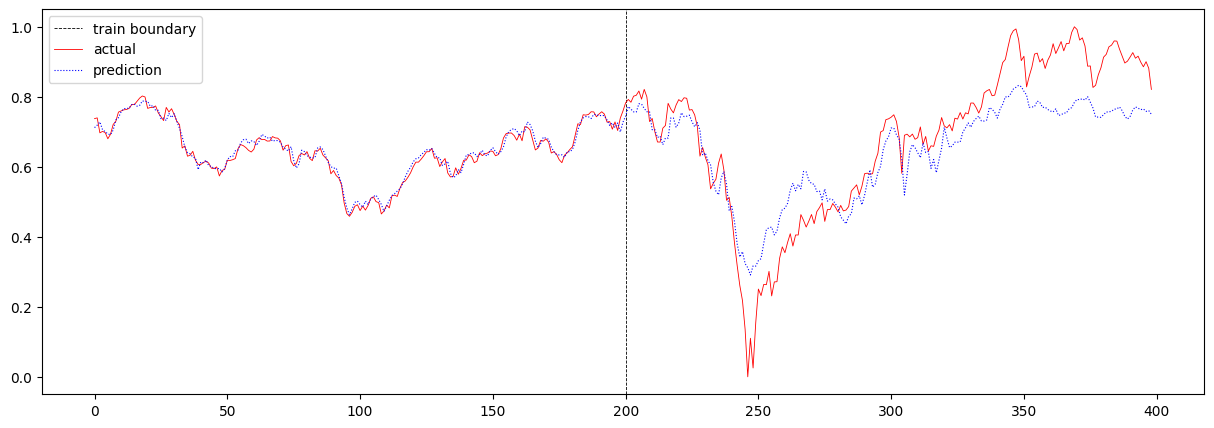
오히려 loss 값이 더 커진 것으로 보아, RNN이 장기 기억을 더 잘 기억하였지만, 장기적인 데이터가 주가 예측에 오히려 방해가 되었다고 결론 내릴 수 있습니다.
LSTM
RNN의 한계
RNN의 목적을 떠올려보자면, 한 sequence 내에서 이전 정보를 기억하여 현재에 반영하는 것이라고 할 수 있습니다. 당연하게도 시간 간격이 길어질수록 이전의 상태를 충분히 기억하지 못합니다. 따라서 많은 맥락을 필요로 하는 경우에 성능이 떨어집니다. 예를 들어서, 구름이 “하늘”에 있다. 라는 문장에서 “하늘”을 추론해야 한다고 가정해봅시다. 이 경우에는 바로 앞의 “구름”이라는 단어만 보아도 충분히 “하늘”이라는 단어를 추론할 수 있을 것입니다. 하지만 나는 한국에서 태어났다. … 나는 “한국어”를 유창하게 구사한다. 라는 긴 문단에서 “한국어”이라는 단어를 추론해야 한다고 가정해봅시다. 이 경우에는 중간의 문장들에 관계없이 가장 앞 문장에 포함된 “한국”이라는 단어를 보아야지 “한국어”라는 단어를 추론할 수 있을 것입니다. 이를 위해선 “한국어”로부터 아주 멀리 떨어진 “한국”이라는 단어를 모델이 기억해야만 가능합니다. 이렇게 긴 맥락을 모델이 기억하는 쉽지 않습니다.
아래 그림은 h3을 추론하기 위해서 가까이에 있는 x0와 x1을 참고하는 상황을 나타내는 그림입니다. 이 경우에는 모델이 짧은 sequence만을 기억해도 되기 때문에 좋은 성능을 낼 수 있을 것입니다.
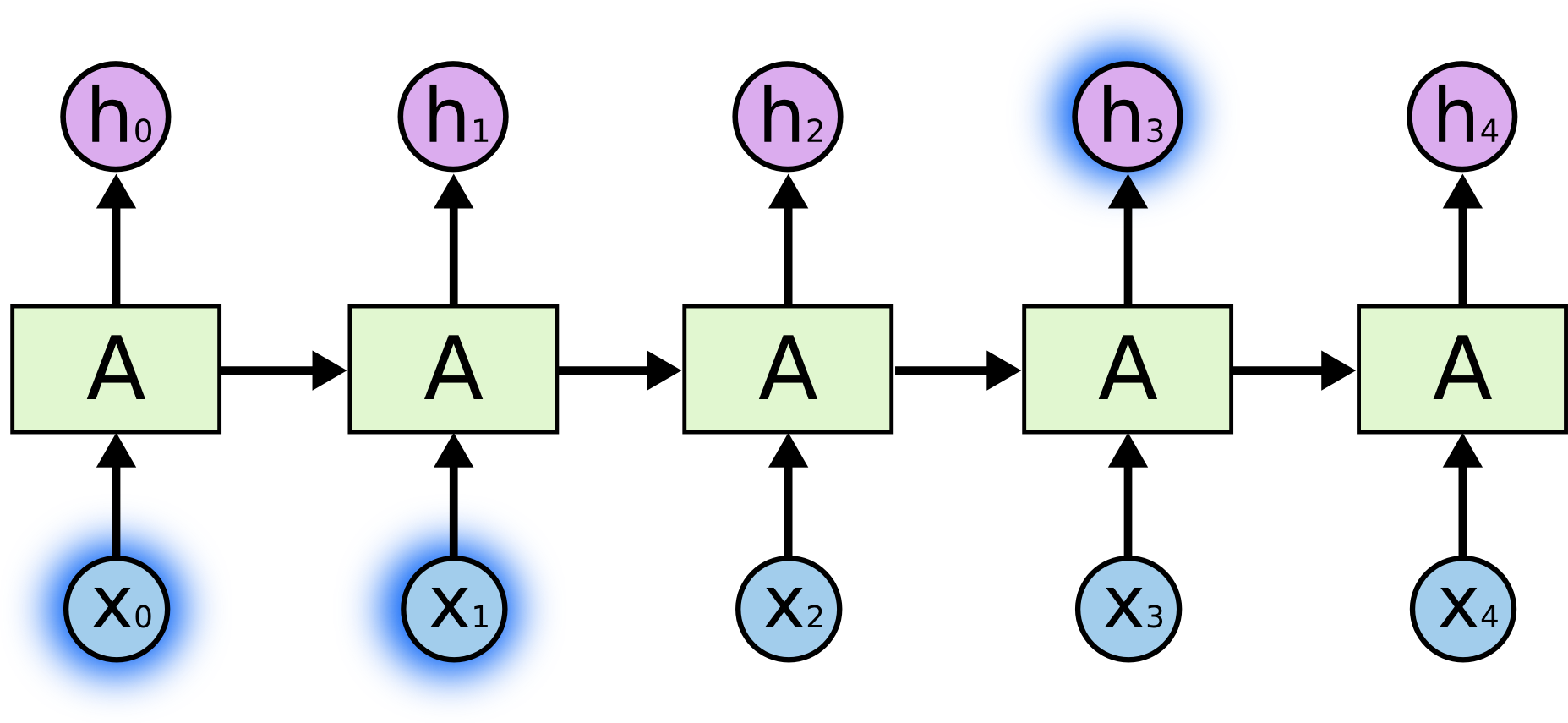
http://colah.github.io/posts/2015-08-Understanding-LSTMs
반면에 아래 그림은 $h_{t+1}$을 추론하기 위해서 멀리있는 x0와 x1을 참고해야 하는 상황을 나타낸 그림입니다. 이 경우에는 모델이 긴 sequence를 기억해야 하는게 이는 RNN에서는 쉽지 않기 때문에 성능이 좋지 못할 것입니다.
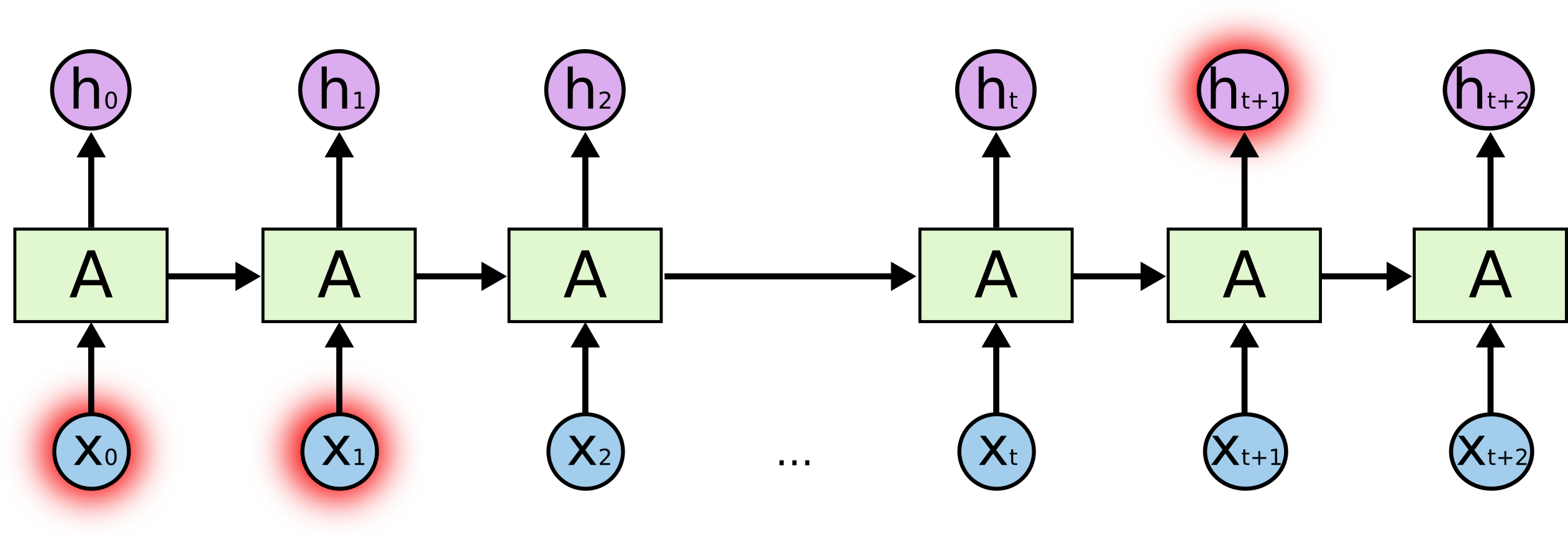
http://colah.github.io/posts/2015-08-Understanding-LSTMs
long-term dependencies
Long-term dependency는 직전 정보와 더불어 먼 과거의 정보를 함께 고려할 수 있는가?에 관한 개념입니다. 먼 과거의 정보에 의존하지 못하는 경우, 즉 먼 과거의 정보를 참고하지 않는 경우 long-term dependencies problem이 있다고 말합니다. RNN에서 long-term dependencies problem이 발생하는 이유는 앞서 알아본 것과 같이 Gradient Vanishing, Gradient Exploding이 발생하기 쉽기 때문입니다.
LSTM에서는 이를 해결해서 장기 기억을 가질 수 있도록 합니다.
overview
LSRM은 1997년 Long Short-Term Memory 이라는 논문에서 제안되었습니다. 한 마디로 정리하자면 RNN이 long-term dependencies를 가지도록 하기 위해 명시적으로 설계된 네트워크라고 설명할 수 있습니다. 현재 LSTM 구조가 많은 개선을 통해 언어, 음성 등의 다양한 분야에서 활용되고 있습니다.
기존 RNN은 하나의 neural network로 구성되어 있지만, LSTM은 서로 상호작용하는 4개의 neural network로 구성되어 있습니다. 아래 그림을 보시면 RNN과 LSTM으 구조가 어떻게 다른지 한눈에 확인하실 수 있습니다.
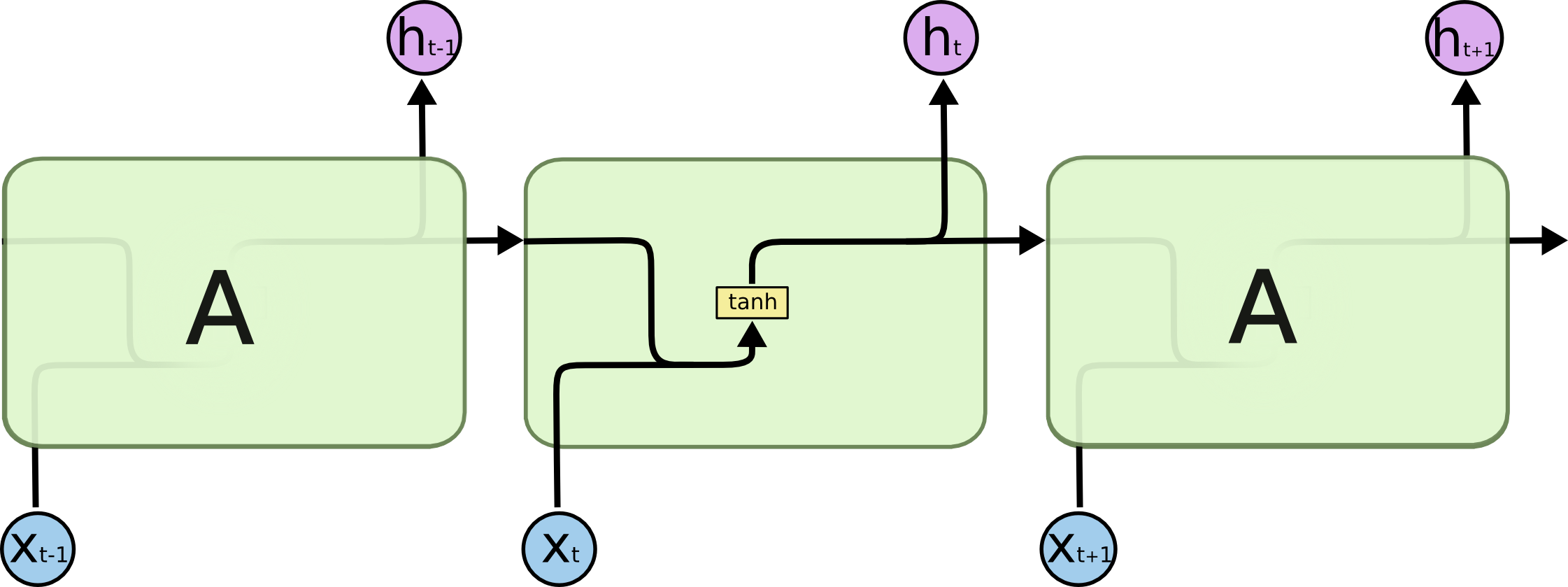
http://colah.github.io/posts/2015-08-Understanding-LSTMs
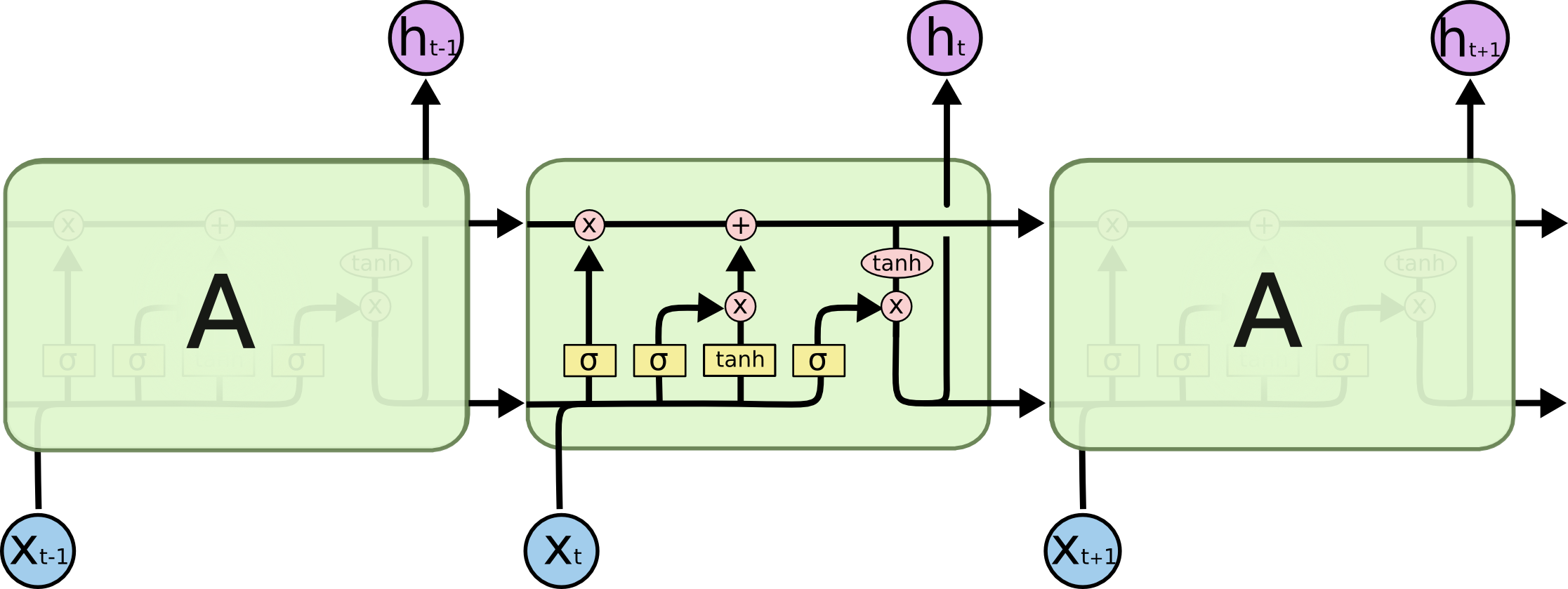
http://colah.github.io/posts/2015-08-Understanding-LSTMs
cell state
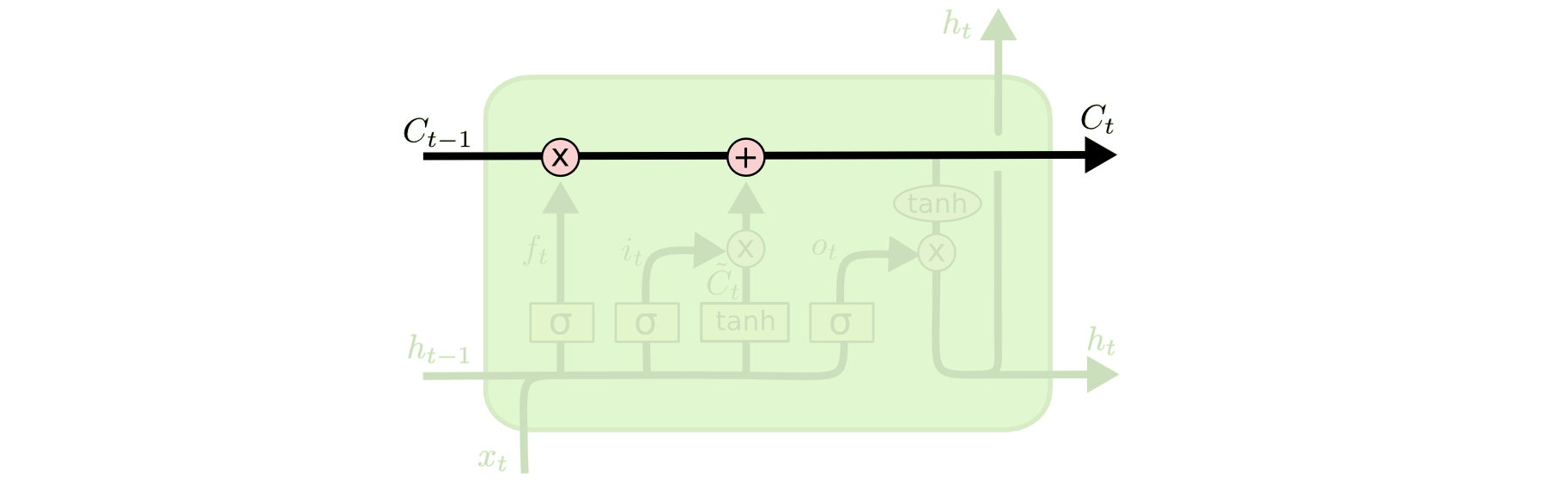
cell state
cell state는 LSTM에서 가장 중요한 개념입니다. 이 개념으로 RNN과 구분되며 높은 성능을 달성할 수 있게 됩니다. cell state에는 작은 linear 연산만을 수행하기 때문에 정보가 잘 변경되지 않고 오래 유지된다는 특성을 가지게 됩니다. cell state의 정보는 3가지 gate에 의해 변경됩니다. 이때 gate라는 표현을 쓰는 이유는 정보가 cell state로 반영되는 문/통로라는 의미에서 gate라고 부르는 것 같습니다.
예를 들어 아래와 같이 Sigmoid 함수와 곱셈으로 이루어진 gate가 있습니다. 이 gate는 Sigmoid 함수의 결과가 0이면 cell state로 아무 정보를 넘기지 말고, Sigmoid 함수의 결과가 1이면 cell state로 모든 정보를 넘기는 기능을 수행합니다.
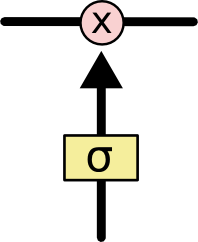
gate example
이제 cell state를 변경하는 3개의 gate들에 대해 하나씩 살펴보겠습니다.
forget gate
forget gate는 정보를 얼마나 남길 것인지 (버릴 것인지)를 결정합니다. 아래 그림에서 확인할 수 있는 것처럼, $h_{t-1}$과 $x_t$를 Sigmoid layer에 넣어서 얻은 $f_t$ (0~1)을 $C_{t-1}$로 보내는 역할을 수행합니다. $C_{t-1}$로 보내진 값이 0이면 $C_{t-1}$을 초기화, 즉 모든 정보를 버리는 것이며, $C_{t-1}$로 보내진 값이 1이면 $C_{t-1}$을 유지, 즉 모든 정보를 유지하는 것입니다.
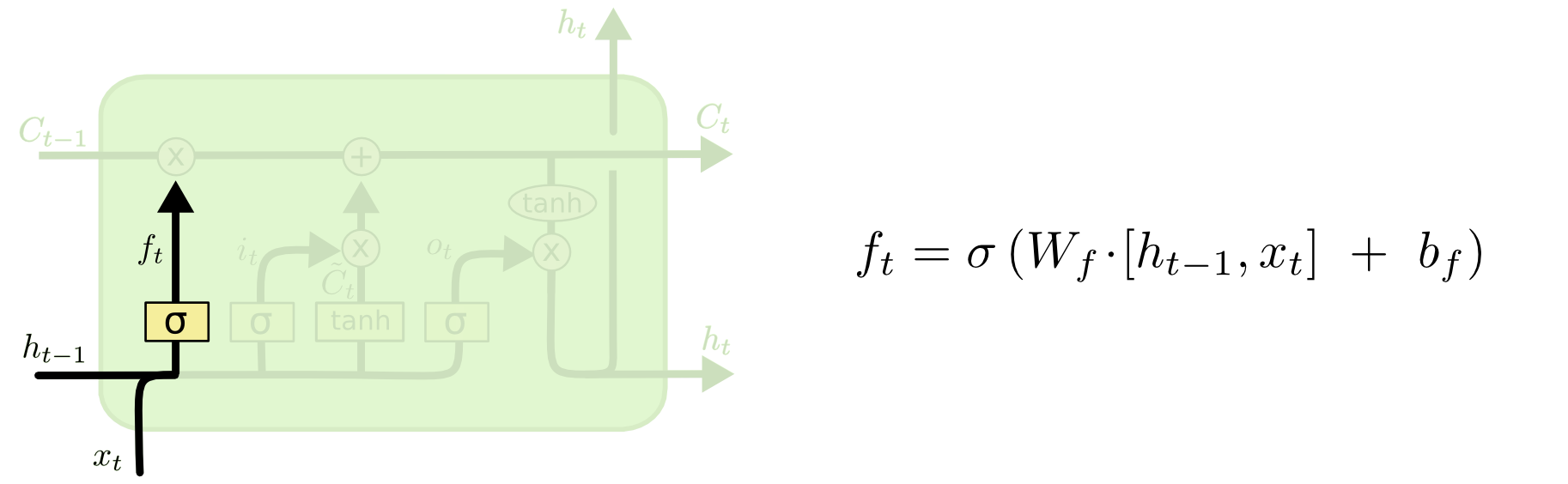
forget gate
input gate
input gate는 새로 들어온 정보를 cell state에 반영합니다. 아래 그림에서 $h_{t-1}$과 $x_t$를 tanh layer에 넣어서 얻은 $\tilde{C}t$은 cell state에 더해질 정보를 의미합니다. $h{t-1}$과 $x_t$를 Sigmoid layer에 넣어서 얻은 $i_t$ (0~1)는 $\tilde{C}_t$를 cell state에 얼마나 반영할지 결정합니다.
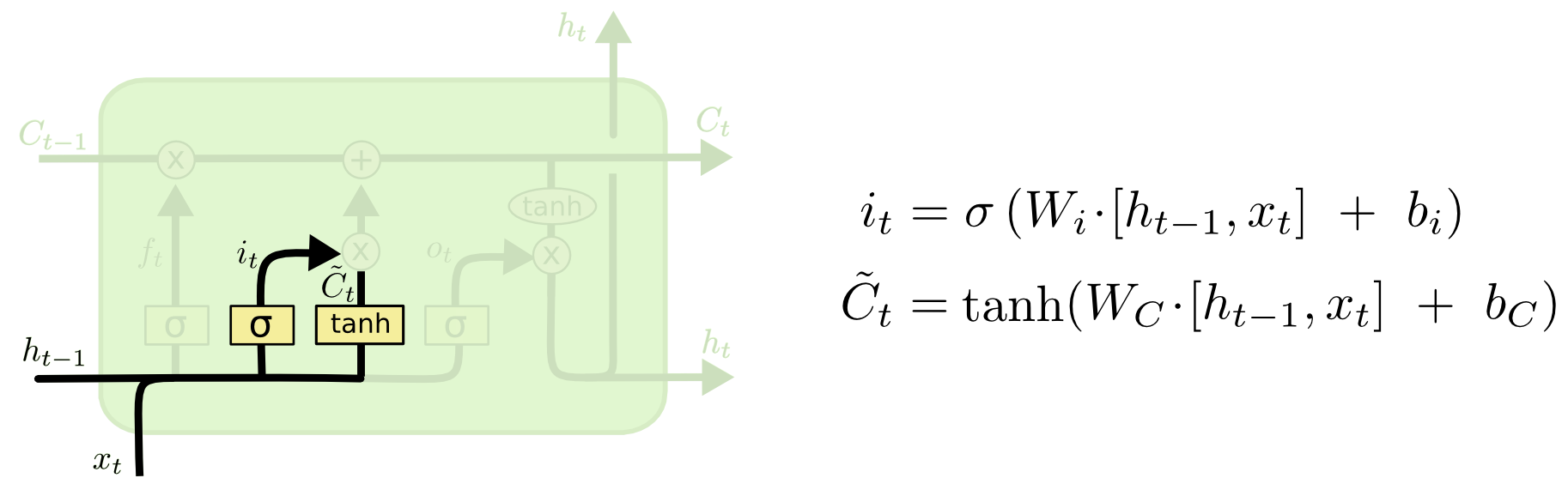
input gate
각 시점에서 forget gate와 input gate의 output에 따라 아래와 같이 cell state를 수정합니다.
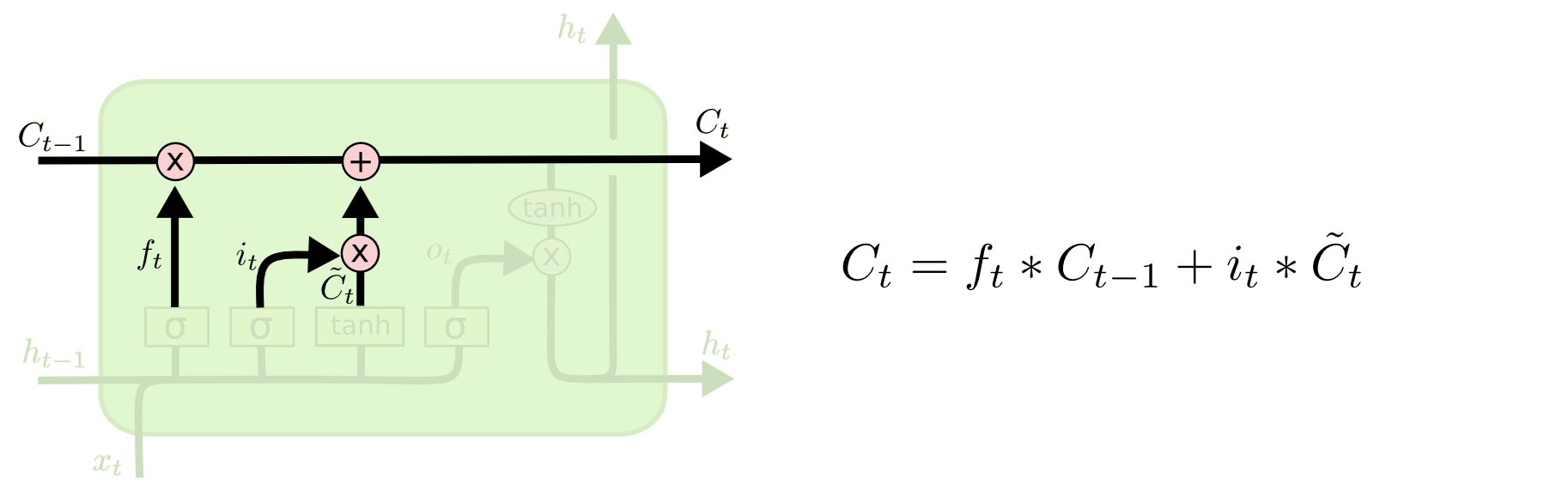
forget gate와 input gate
output gate
output gate는 말그대로 output $h_t$를 결정합니다. 아래 그림에서 $h_{t-1}$과 $x_t$를 Sigmoid layer에 넣어서 얻은 $o_t$ (0~1)는 output $h_t$에 현재 update된 cell state $C_t$를 얼마나 반영할지 결정합니다.
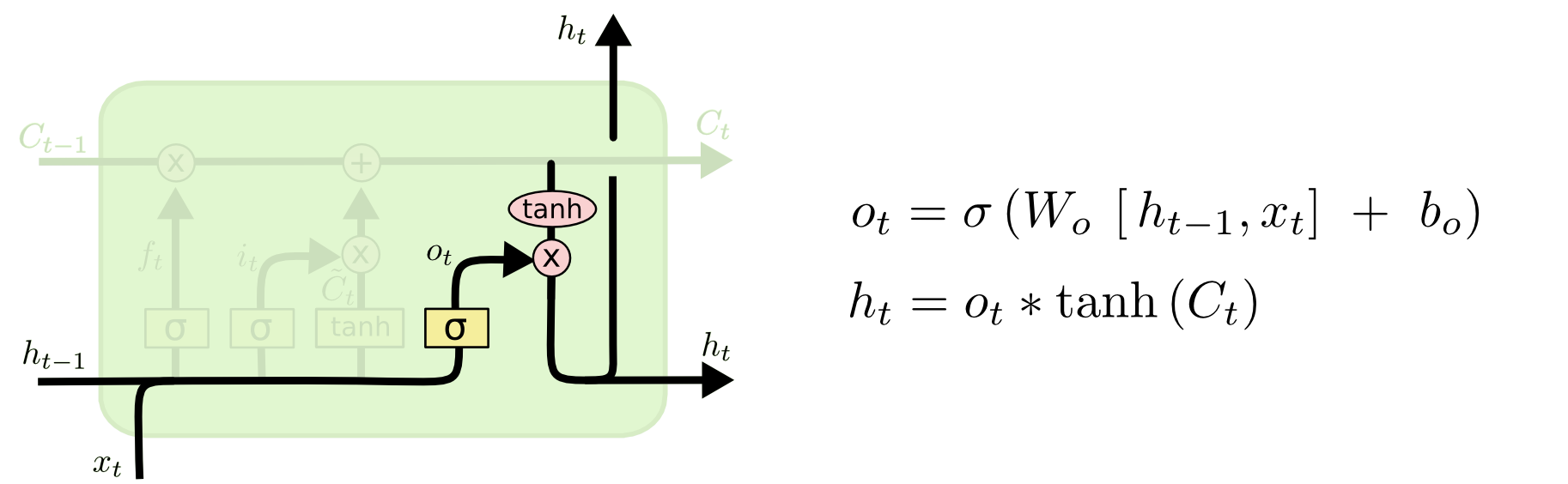
output gate
지금까지 알아본 3개의 gate를 그림으로 정리하자면 아래와 같습니다.
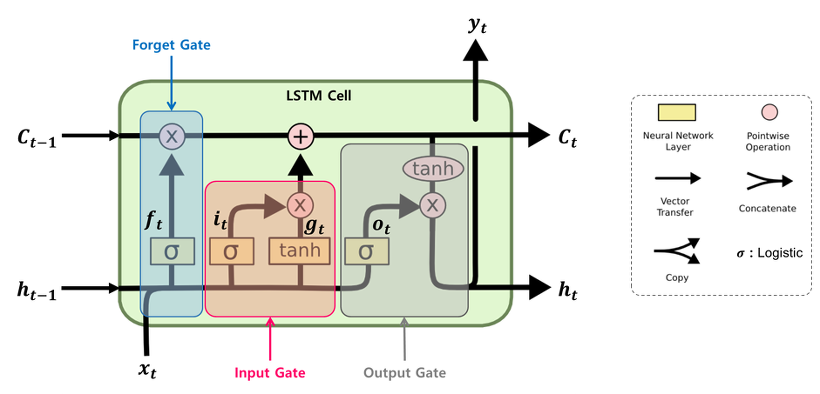
3 gates
LSTM의 long-term dependencies

back propagation을 위해 cell state $C_T$를 $C_t$에 대해 미분해보면 아래와 같습니다. $(T>t)$
$\frac{\partial C_{T}}{\partial C_{t}} = \frac{\partial C_{T}}{\partial C_{T-1}} * \frac{\partial C_{T-1}}{\partial C_{T-2}} * … * \frac{\partial C_{t+1}}{\partial C_{t}}$
$\frac{\partial C_{T}}{\partial C_{T-1}}=f_{T}, \frac{\partial C_{T-1}}{\partial C_{T-2}}=f_{T-1}, … , \frac{\partial C_{t+1}}{\partial C_{t}}=f_{t+1}$
$\frac{\partial C_{T}}{\partial C_{t}}=\prod_{i=t+1}^{T}{f_{i}}$
$f$는 Sigmoid layer의 output이므로 (0,1)의 값을 가집니다. $f$가 1보다 큰 값을 가질 수 없으므로 gradient exploding이 발생하지 않습니다. $f$가 1에 가까울수록 gradient vanishing이 최소화되며 cell state를 많이 유지하기 때문에 long term memory를 많이 유지하게 됩니다.
위와 같이 cell state에 대한 미분값에서 Gradient Vanishing, Gradient Exploding이 발생할 가능성이 낮기 때문에 LSTM는 long-term dependencies를 가질 수 있게 됩니다.
다음으로는 다양한 LSTM의 구조적인 변형 중 몇 가지를 알아보겠습니다.
peephole connection
peephole connection은 2000년에 Recurrent Nets that and Count 이라는 논문에서 제안되었습니다. 이 구조에서는 3가지 gate의 Sigmoid layer의 input으로 $h_{t-1}$과 $x_t$와 더불어 cell state를 함께 사용합니다. 각 gate 마다 peephole connection의 사용 유무를 결정할 수도 있습니다. 실험적으로 peephole connection을 사용하면 더 많은 맥락을 인식할 수 있다고 합니다.
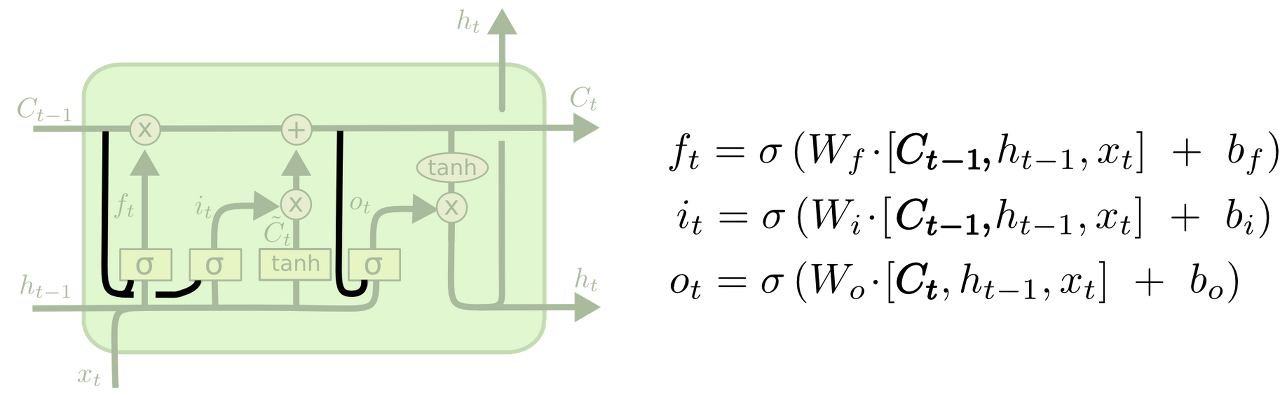
peephole connection
forget gate + input gate
$\tilde{C}_t$를 cell state에 얼마나 반영할지 결정하는 $i_t$를 따로 계산하지 않고 $1-f_t$로 사용하는 구조도 가능합니다.
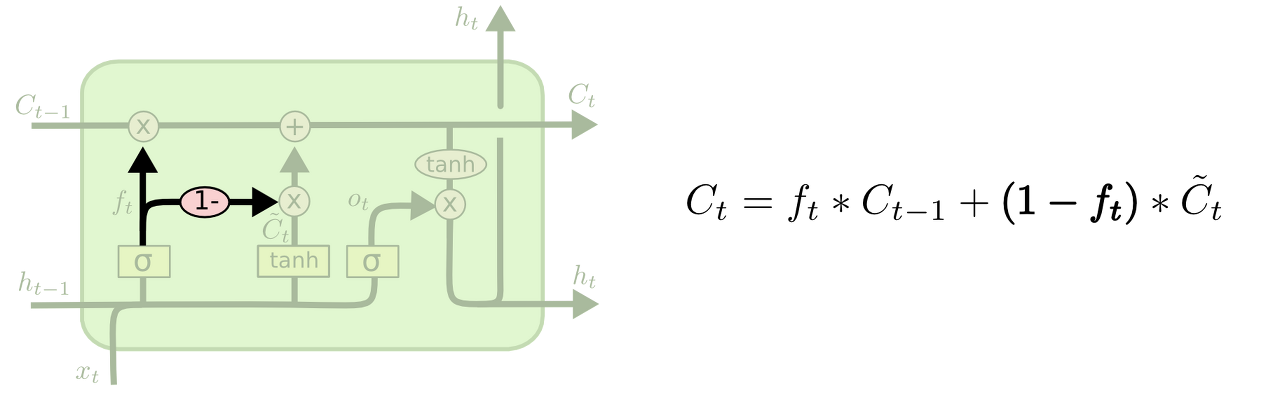
forget gate + input gate
GRU (Gated Recurrent Unit)
마지막으로 GRU는 2014년에 Learning Phrase Representations using RNN Encoder-Decoder for Statistical Machine Translation 이라는 논문에서 제안되었습니다. forget gate와 input gate를 update gate라는 하나의 gate로 합쳤으며, cell state와 hidden state를 하나로 합쳐 hidden state만을 사용합니다. 따라서 LSTM보다 단순한 구조를 가지게 됩니다. 그럼에도 GRU는 LSTM보다 좋은 성능을 보이며, sequence model이 필요한 경우 대표적으로 사용되고 있습니다.

GRU
LSTM 구현
RNN에서와 마찬가지로 2019-01-30부터 2020-10-30까지의 코스피 주가 데이터를 사용하여 미래 주가를 예측하는 간단한 LSTM 모델을 구현해보았습니다. 코드와 결과는 https://www.kaggle.com/code/junhyeog/lstm-kospi에서 확인하실 수 있습니다.
baseline 모델 및 학습을 위한 코드는 아래와 같습니다.
batch_size = 64
test_ratio = 0.5
sequence_length = 4
train_dataset, test_dataset, train_loader, test_loader = build_data(
x, y, batch_size, test_ratio, sequence_length
)
model = LSTM(
input_size=5,
hidden_size=8,
output_size=1,
seq_len=sequence_length,
num_layers=2,
device=device,
).to(device)
criterion = nn.MSELoss()
optimizer = optim.Adam(model.parameters(), lr=1e-3)
train(model, criterion, optimizer, train_loader, num_epochs=1000)
test(model, criterion, train_dataset, test_dataset, sequence_length, batch_size)
baseline 모델의 total loss는 0.002735057533884953 이며, 주가 예측 결과는 아래와 같습니다.
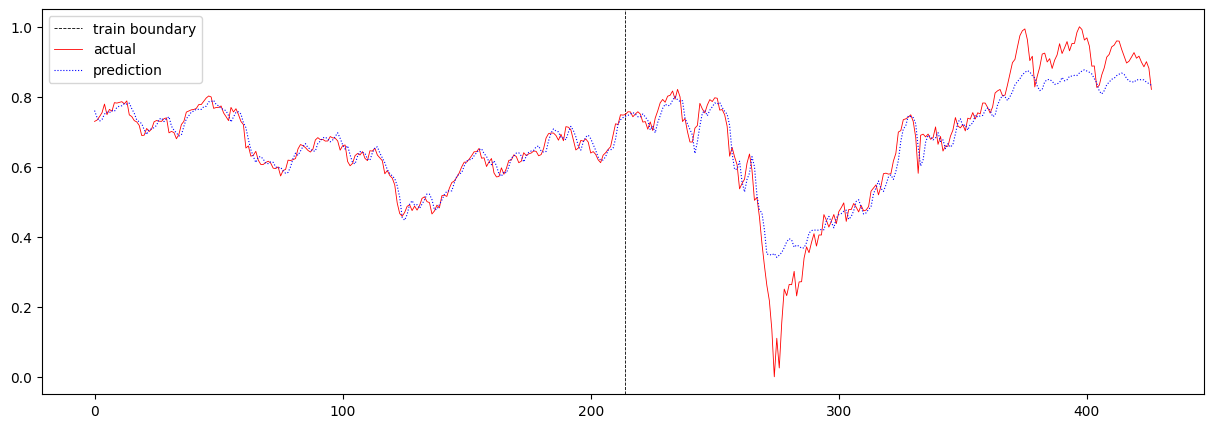
다음으로 sequence 길이를 4에서 16으로 증가시켜보았습니다. 여기서 sequence 길이란 T의 값을 의미합니다. 이 때의 total loss는 0.004116482209480766이며, 주가 예측 결과는 아래와 같습니다.
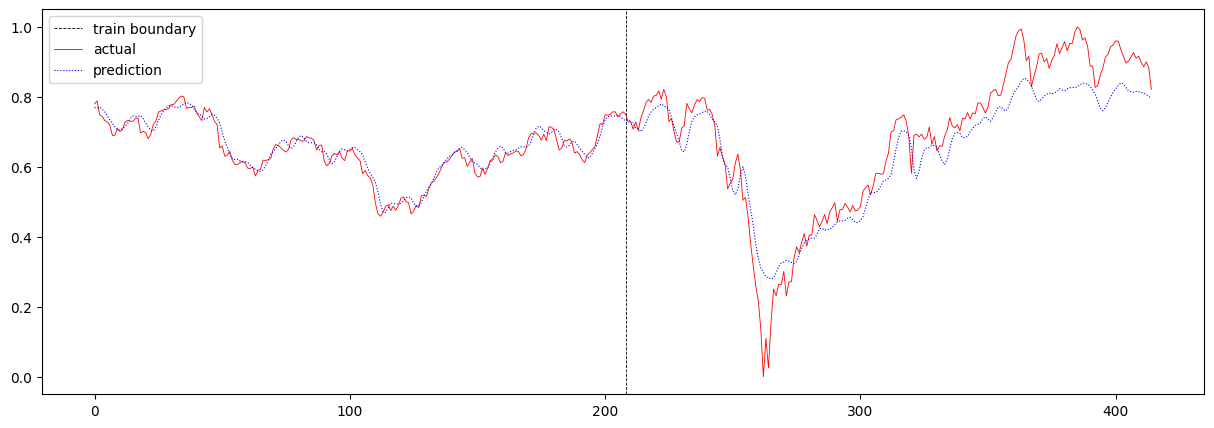
T를 증가시켰더니 RNN에서와 마찬가지로 loss가 증가하였습니다. RNN보다 장기 기억을 더 잘 학습하는 LSTM에서도 loss가 증가하였음으로 주가 예측에 있어서 이전 16일 간의 데이터를 보고 예측하는 것보다, 이전 4일 간의 데이터를 보고 예측하는 것이 더 정확하다고 해석하는 것이 조금 더 신빙성이 있어졌습니다.
그 다음, sequence 길이를 16에서 32로 더 크게 증가시켜보았습니다. 이때의 total loss는 0.015937334427560148이며, 주가 에측 결과는 아래와 같습니다.
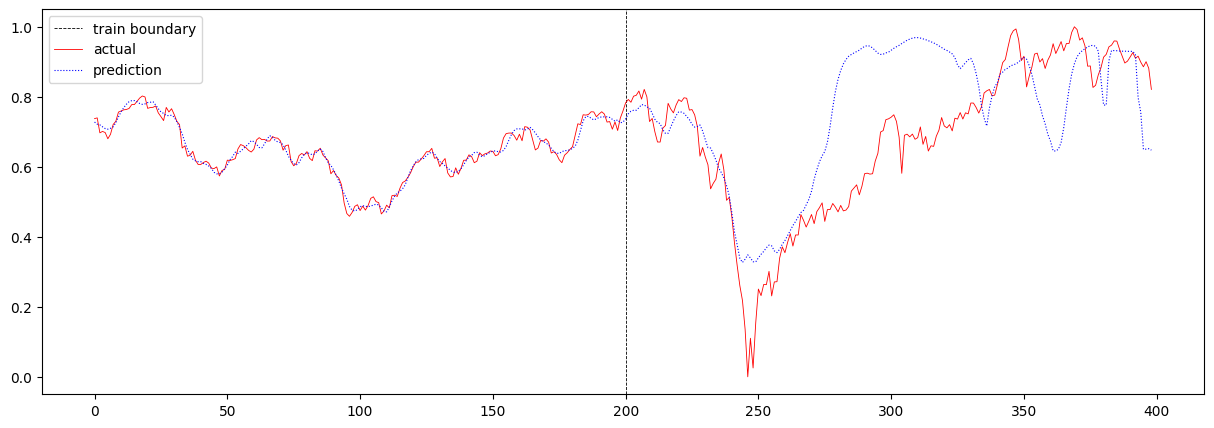
RNN에서는 T가 16일 때와 크게 다르지 않은 결과가 나왔던 반면, LSTM에서는 loss가 크게 증가하였고, 예측이 많이 잘못되었음을 확인할 수 있습니다.
마지막으로 T가 32인 상황에서 LSTM의 scale을 증가시켜보았습니다. hidden layer의 수를 2개에서 4개로 늘렸고, hidden size를 8에서 16으로 늘렸습니다. 이때의 total loss는 0.023485246928300643이며, 주가 예측 결과는 아래와 같습니다.
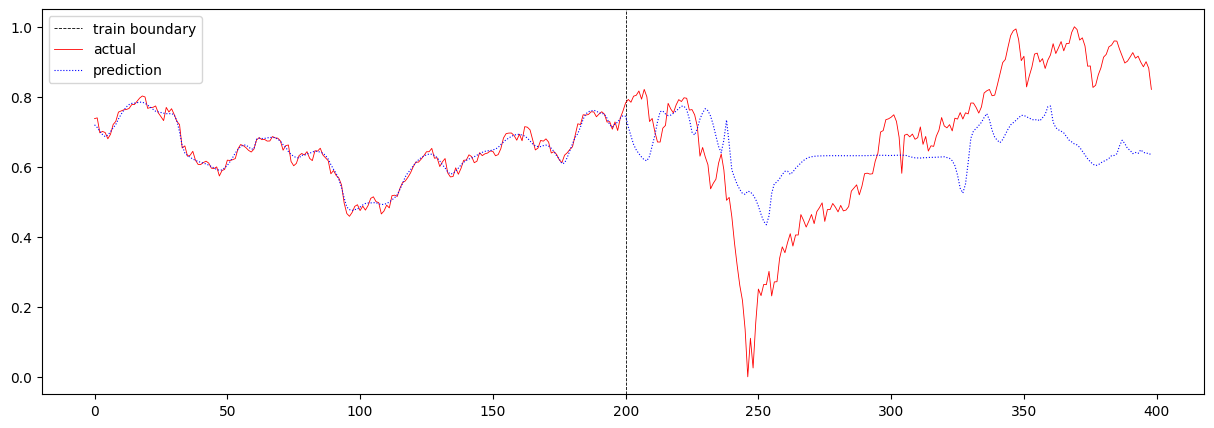
RNN에서와 마찬가지로 오히려 loss 값이 더 커진 것으로 보아, LSTM이 장기 기억을 더 잘 기억하였지만 그로 인해 일관성있는 예측을 보여주어 제대로 된 예측을 하지 못하는 것을 확인할 수 있습니다.
Seq2seq model
이어서 RNN과 LSTM에 이어서 이를 기반으로 하는 seq2seq model에 대해서 알아보겠습니다.
seq2seq model overview
seq2seq model은 하나의 sequence를 입력으로 받아서 또 다른 sequence를 출력하는 구조입니다. 이 모델이 제안된 논문은 아래와 같습니다.
- Sequence to Sequence Learning with Neural Networks (Sutskever et al., 2014)
- Learning Phrase Representations using RNN Encoder–Decoder for Statistical Machine Translation (Cho et al., 2014)
seq2seq model을 그림으로 나타내면 아래와 같습니다. 3개의 데이터로 이루어진 sequence 데이터가 input으로 주어지고, 4개의 데이터로 이루어진 sequence 데이터가 output으로 출력됩니다. 여기서 알 수 있는 점은 input과 output 데이터의 길이가 달라도 된다는 점입니다.


encoder and decoder
seq2seq model은 encoder와 decoder로 이루어집니다.
encoder는 입력된 정보를 처리해서 저장(압축)하는 역할을 합니다. 다시 말해 input sequence의 각 item을 처리해서, 그 안의 정보들을 하나의 vector (context)로 표현합니다. encoder가 input sequence의 모든 item에 대한 처리를 끝냈다면, context를 decoder로 전달합니다.
decoder는 encoder의 출력값을 해석(출력)하는 역할을 합니다. encoder로부터 전달받은 context를 처리해서 output sequence의 각 item을 순차적으로 생성합니다.
encoder와 decoder에는 RNN, LSTM, GRU 등과 같은 RNN 계열의 network가 사용됩니다. 따라서 input sequence의 item이 처리될 때마다 output과 hidden state가 update되며 최종 (input sequence의 마지막 item에 대한) hidden state가 context가 되어 decoder에 전달되게 됩니다.
단순하게 seq2seq model은 RNN 계열의 network를 사용해서 sequence 데이터를 다루는 모델이라고 정리할 수 있습니다.
Attention
기존 seq2seq model의 문제점
일반적인 seq2seq model에서는 context가 bottleneck이 됩니다. context는 input sequence의 마지막 item에 대한 hidden state이기 때문에 input sequence의 뒷부분 item들에 영향을 많이 받으며 앞부분 item들의 정보를 많이 담지 못합니다. 또한 LSTM이나 GRU가 기본 RNN보다는 long-term dependency 관점에서 좋은 성능을 보이지만 근본적인 한계가 존재합니다.
이러한 문제점이 존재하는 상황에서 긴 sequence를 처리하기 위해서 attention이라는 개념을 사용합니다. attention을 통해 model은 input sequence의 item들 중에서 현재 output item이 주목해야하는 item이 무엇인지 알 수 있습니다.
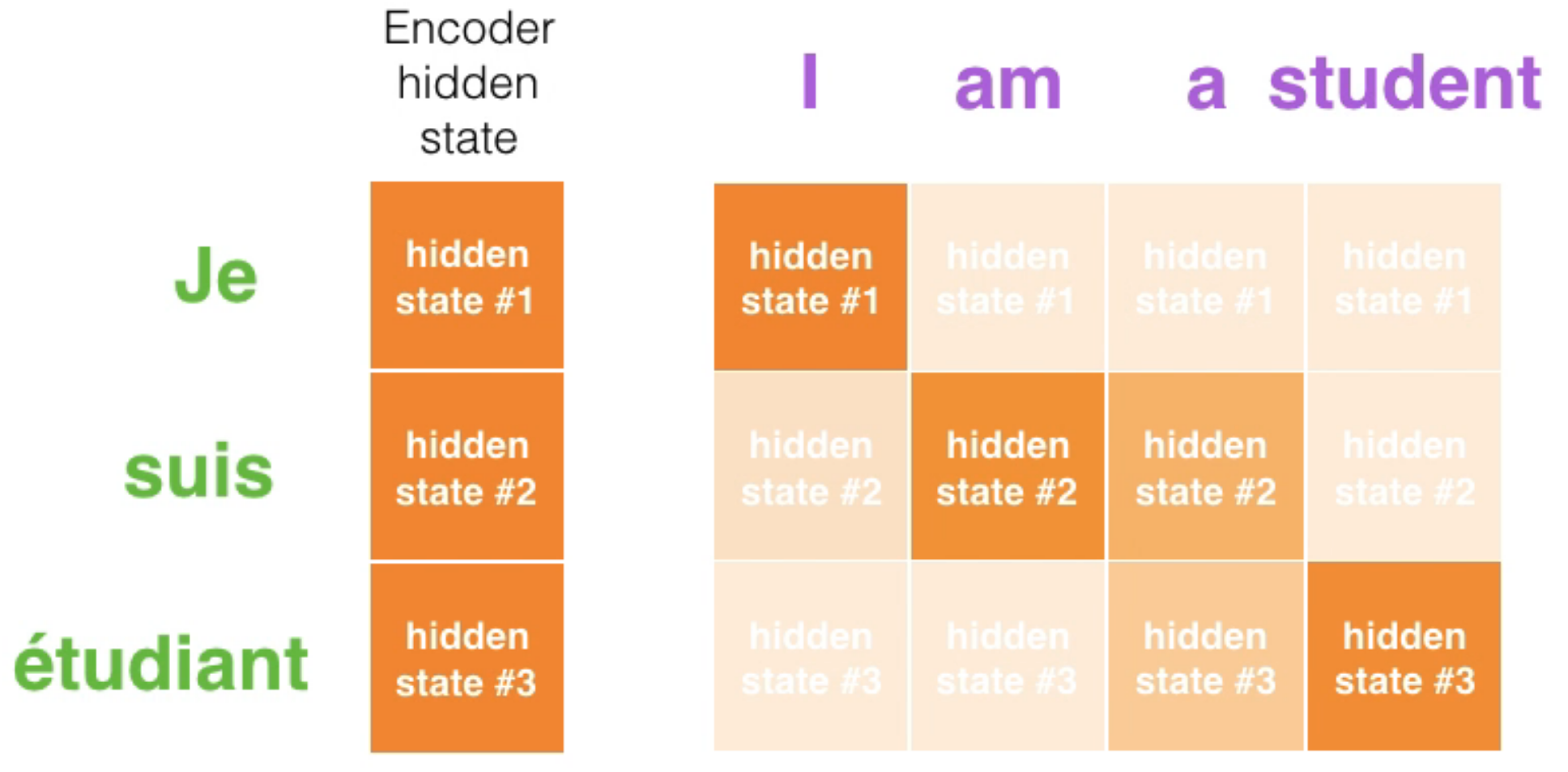
예를 들어 아래 그림에서 student라는 단어를 생성할 때 불어로 student와 뜻이 같은 3번째 단어에 더 집중하면 더 좋은 성능을 달성할 수 있을 것입니다.
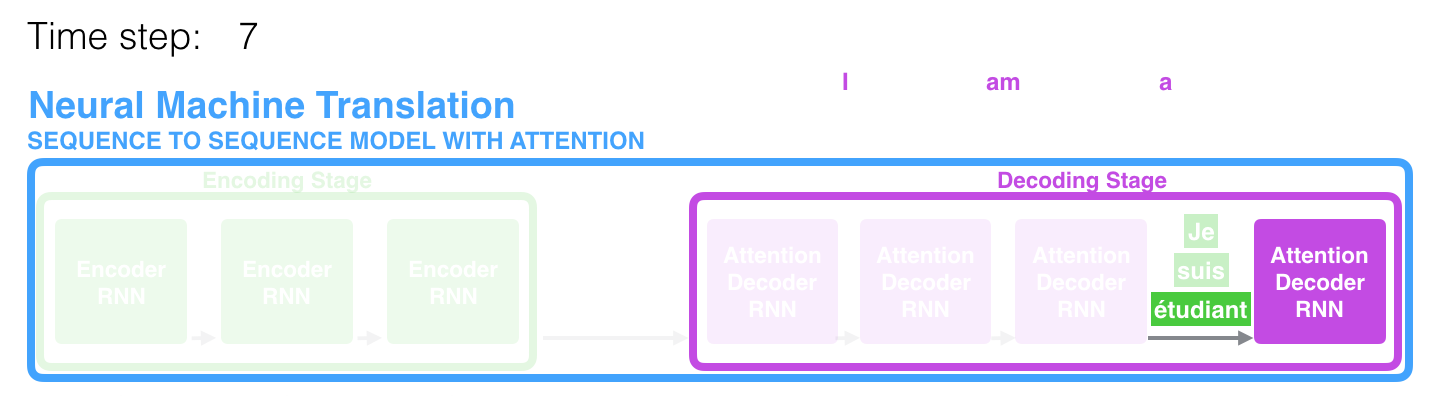
아래 그림을 보면 I am a student 4개의 단어를 각각 50%, 30%, 10%, 10%만큼 참고(attention)해서 Je라는 단어를 추론하게 되는 것입니다.
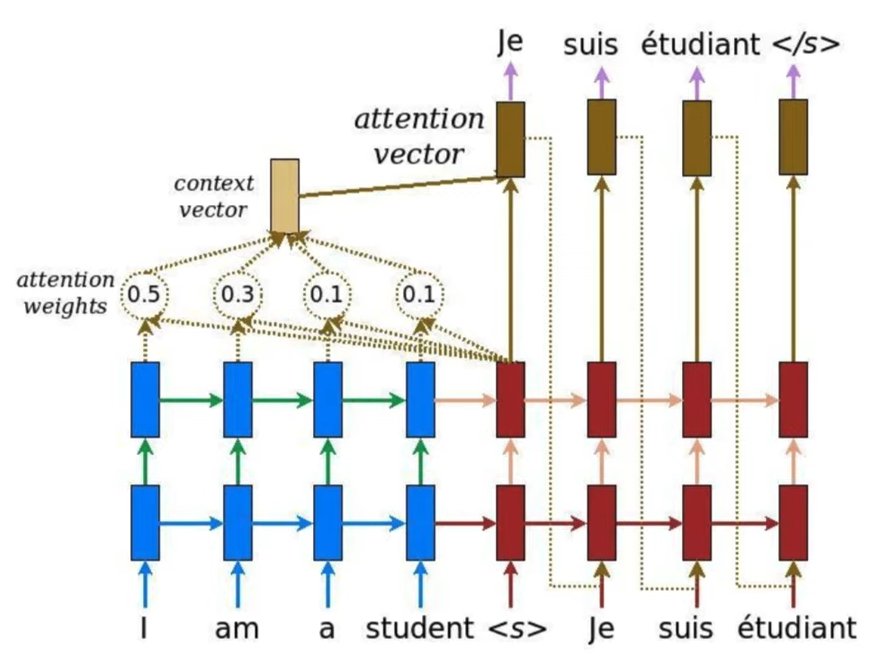
Attention의 종류
attention에는 크게 아래 2가지가 있습니다.
- Bahadanau attention (Bahdanau et al., 2014)
- https://arxiv.org/abs/1409.0473
- attention score가 따로 학습됨 (neural network 존재)
- Luong attention (Luong et al., 2015)
- https://arxiv.org/abs/1508.04025
- attention score가 따로 학습되지 않음
두 방식의 성능 차이가 크지 않기 때문에 주로 Luong의 방식을 사용합니다.
Attention in seq2seq model
attention을 seq2seq model에 적용했을 때 달라지는 점
먼저 아래 그림과 같이 encoder의 마지막 hidden state를 전달하는 것이 아닌, 모든 item에 대한 hidden state들을 전달합니다.
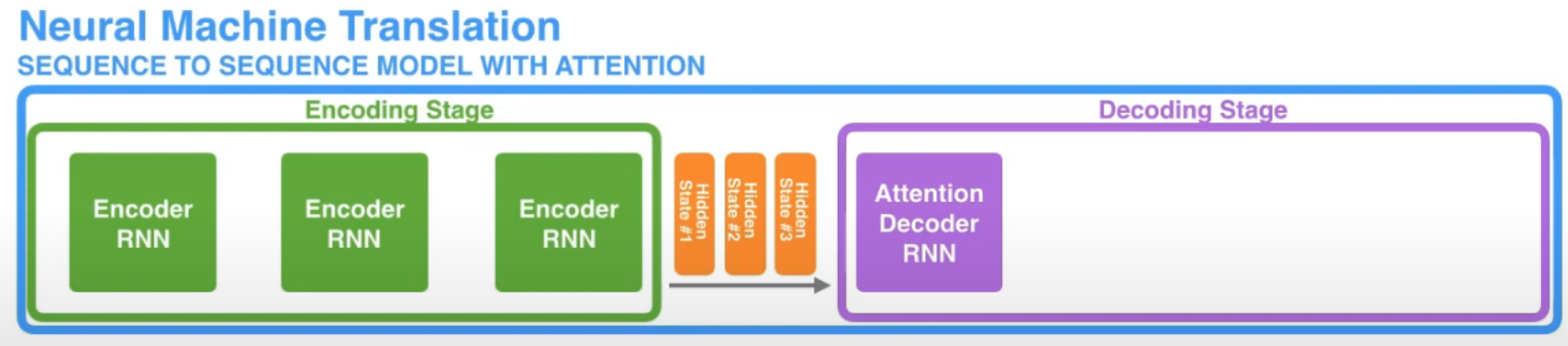
그리고 decoder가 output을 생성하기 위해 추가적인 step을 거쳐야 합니다. decoder가 현재 output을 생성하기 위해서 아래 step을 거치게 됩니다.
- encoder로부터 전달받은 전체 hidden state를 살펴본다. (LSTM이나 GRU를 사용하더라도 각 hidden state는 이전 context보다는 자신과 가까운 context에 대한 정보를 더 많이 가지고 있음)
- 각 hidden state에 점수(attention score or weight)를 매긴다. (방법은 여러가지 존재)
- 점수들에 softmax를 취해서 이것을 각 hidden state에 곱해서 더한다. (그 output이 context vector이며, attention score가 높은 hidden state의 정보가 많이 반영될 것임)
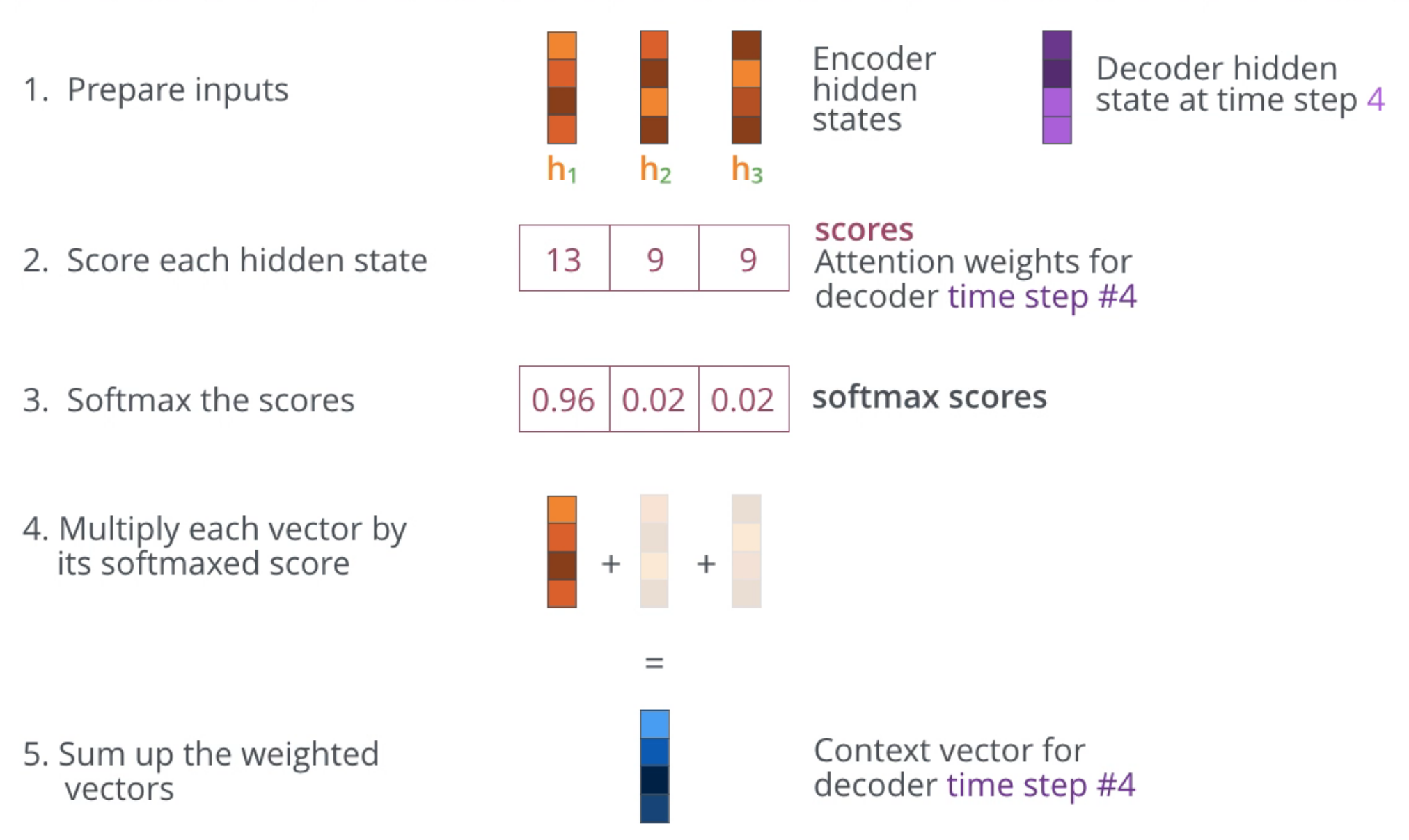
- 계산된 context vector와 현재 hidden state를 concat하여 feedforward layer의 input으로 넣는다.
- feedforward layer의 output이 현재 step의 output이 된다.
위 과정을 아래 그림과 함께 이해하면 도움이 될 것입니다.
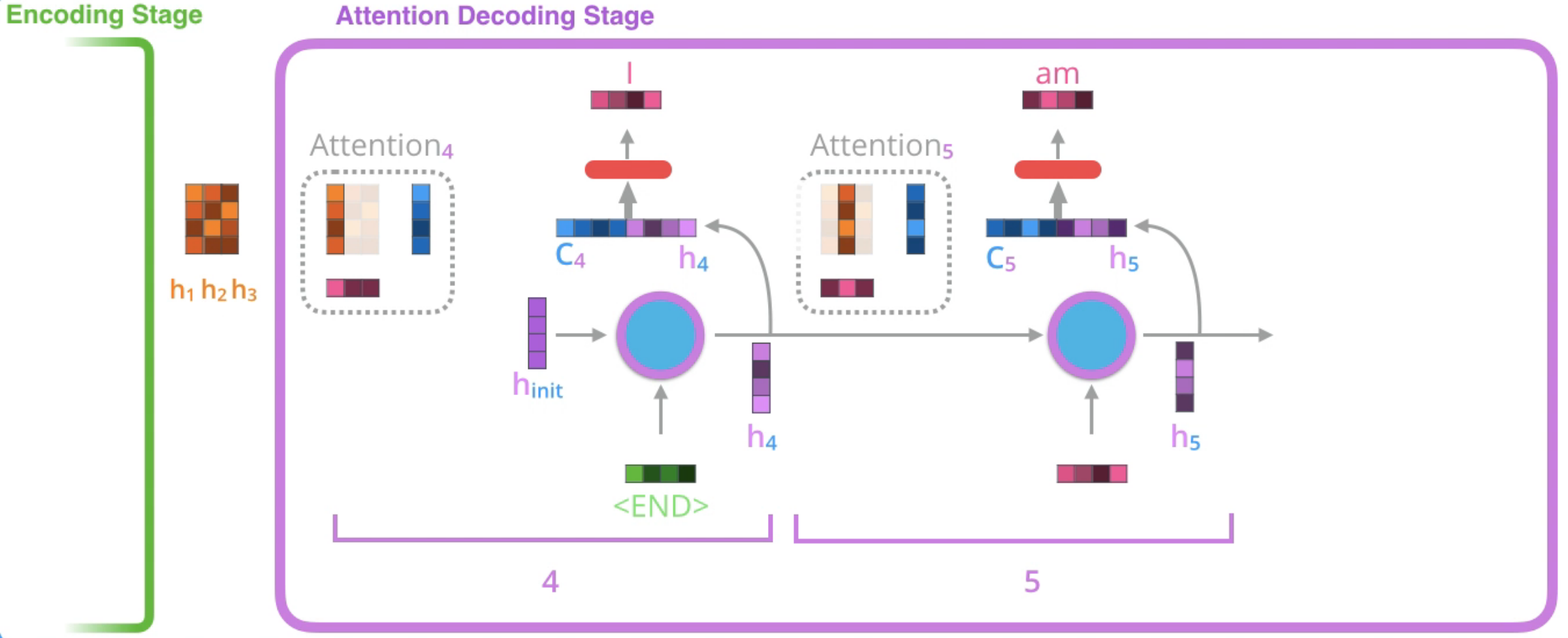
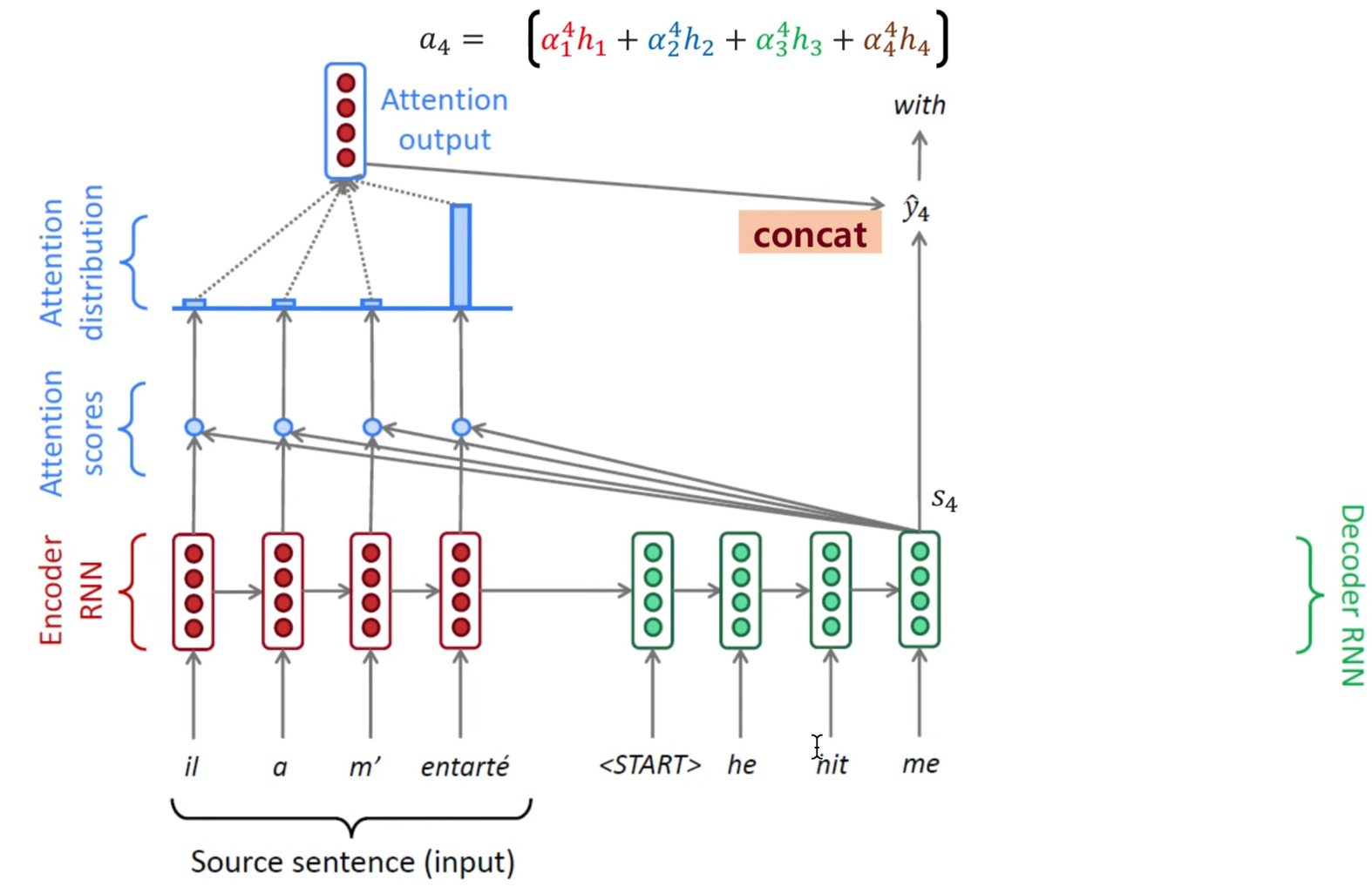
attention score
학습된 attention score를 보면 모델이 제대로 학습이 되었는지 알 수 있으며 설명 가능하게 됩니다. 예를 들어 아래와 같이 기계 번역의 task에서 같은 뜻을 가지는 단어 간의 attention score이 높아야 합니다.
마찬가지로 아래 그림을 보면 단어의 순서대로 attention하는 것처럼 보이지만, 어순이 다른 부분인 “European Economic Area”과 “européenne économique zone”은 반대의 순서로 attention하게 됩니다.

attention의 장점
attention 개념을 활용하면 seq2seq model의 bottleneck problem 해결할 수 있게 됩니다. 또한 gradient vanishing problem 완화하며, attention score를 통해 interpretability를 제공합니다.
general definition of attention
attention은 seq2seq model 이외에도 다른 model들에도 적용 가능한 개념입니다. attention을 광범위하게 정의하자면 query vector와 value vector들이 존재할 때, query에 기반해 value들의 weighted sum을 계산하는 기법으로 정의할 수 있습니다. 예를 들어 seq2seq model에서는 query는 각 decoder hidden state를 의미하고 values는 모든 encoder hidden state들을 의미하게 됩니다.
Conclusion
지금까지 RNN부터 LSTM, Seq2Seq, Attention까지 시계열 데이터 분석에 활용되는 개념들을 발전 순서에 따라서 정리해보았습니다. 현재를 기준으로 많이 과거의 방법론이지만 한 분야가 어떻게 발전해왔는지를 시간 순서로 알아보니 개념을 잡는데 큰 도움이 되는 것 같습니다.
Reference
- https://www.nature.com/articles/323533a0
- https://pytorch.org/docs/stable/generated/torch.nn.RNN.html
- https://www.kaggle.com/code/junhyeog/rnn-kospi
- https://ieeexplore.ieee.org/abstract/document/6795963
- https://dl.acm.org/doi/10.1162/neco.1997.9.8.1735
- https://arxiv.org/abs/1406.1078
- https://ieeexplore.ieee.org/abstract/document/861302
- http://colah.github.io/posts/2015-08-Understanding-LSTMs/
- https://pytorch.org/docs/stable/generated/torch.nn.LSTM.html
- https://www.kaggle.com/code/junhyeog/lstm-kospi
- https://arxiv.org/abs/1409.3215
- http://emnlp2014.org/papers/pdf/EMNLP2014179.pdf
- https://arxiv.org/abs/1409.0473
- https://arxiv.org/abs/1508.04025
- https://tutorials.pytorch.kr/intermediate/seq2seq_translation_tutorial.html