IND-CCA2 Encryption schemes and Fujisaki-Okamoto transform
Introduction
암호의 안전성
암호는 수천년 전에 로마나 고대 그리스에서 사용하던 고전암호로부터 시작해 20세기 초에는 상당히 발전되어 전쟁에서 사용되기도 했으며, 그 후 현재까지 쓰이고 있는 대칭키 암호(symmetric key cryptography) 및 공개키 암호(public key cryptography)가 개발되었습니다. 현재는 그 외에도 Lattice-based cryptography 등의 여러 암호가 활발하게 연구되고 있습니다.
초창기의 암호 중 몇몇은 하나의 문자가 하나의 문자에 대응되는 형식을 띠고 있습니다. 이러한 암호의 경우 문자마다 실제 단어에 사용되는 빈도가 달라 암호문이 충분히 주어진다면 그 빈도를 파악하여 대응되는 문자를 파악하여 해독하는 것이 가능합니다.
이처럼 암호 시스템을 설계하더라도 그 보안성이 충분하지 못할 수 있기 때문에 암호가 얼마나 안전한지 판단하는 기준의 필요성이 대두되었습니다.
암호 공격 모델
여러가지 암호 공격을 모델링하여 각 암호가 어떤 암호 공격으로부터 안전한지에 따라 그 암호의 보안 레벨을 확인할 수 있습니다.
암호 공격은 공격자(attacker)가 할 수 있는 행동에 따라 구분합니다. 대표적인 예시는 다음과 같습니다.
ciphertext only attack(COA): 공격자에게는 암호문만이 주어집니다.
know plaintext attack(KPA): 공격자는 몇 개의 (평문, 암호문) 쌍을 가지고 있습니다.
chosen plaintext attack(CPA): 공격자에게 임의의 plaintext를 encrypt할 수 있는 oracle(encryption oracle)이 주어집니다.
chosen ciphertext attack(CCA): 공격자에게 encryption oracle이 주어지고, 또한 자신이 해독하고자 하는 메시지에 대한 ciphertext를 제외한 ciphertext를 decrypt할 수 있는 oracle(decryption oracle)이 주어집니다.
Ciphertext indistinguishability
Ciphertext indistinguishability는 공격자가 본인이 제시한 두 plaintext $m_0, m_1$에 대한 ciphertext $c_0, c_1$를 받았을 때, 각 ciphertext가 어떤 plaintext를 암호화한 것인지 구분할 수 없음을 뜻합니다.
공격자가 chosen plaintext attack을 할 수 있을 때 위 성질이 보장되는 암호를 IND-CPA secure한 암호, chosen ciphertext attack을 할 수 있을때도 보장되는 암호를 IND-CCA secure한 암호라고 합니다.
CCA에는 두 가지 종류가 있는데, 하나는 공격자가 자신이 사용한 오라클에 대한 결과에 따라 적응적으로(adaptive) 판단하여 오라클을 호출할 수 없다는 제약 조건이 있는 경우입니다. 이를 lunchtime attack이라고도 부르며, 이에 대해 안전한 암호를 IND-CCA1 secure하다고 합니다. 다른 하나는 그러한 제약 조건이 없는 경우로, 이 공격에 대해 Ciphertext indistinguishable한 암호를 IND-CCA2 secure하다고 합니다.
당연하게도 IND-CPA, IND-CCA1, IND-CCA2는 뒤로 갈수록 만족하기 어려운 조건이고, 이러한 측면에서 IND-CCA2 암호는 암호 공격 모델에서 상당히 안전하다고 볼 수 있을 것입니다.
Ciphertext indistinguishability - Definition with game
앞서 정의한 Ciphertext indistinguishability는 엄밀하지 못하게 설명한 부분이 있습니다. IND-CCA2 Public Key Encryption이 어떤 조건을 만족해야 하는지, 암호 시스템을 공격하는 공격자 Alice와 안전성을 증명하고자 하는 Bob이 하는 간단한 게임으로 보다 엄밀하게 정의해도록 하겠습니다.
- Bob은 공개키-비밀키 페어 $(pk, sk)$를 생성하고 $pk$를 공개합니다.
- Alice는 Decryption / Encryption Oracle을 사용하고 싶은만큼 사용하여 ciphertext를 decrypt하거나 plaintext를 encrypt할 수 있습니다.
- Alice는 두 plaintext $m_0, m_1$를 Bob에게 전송합니다.
- Bob은 0 또는 1인 random bit $b$를 뽑아 $m_b$를 암호화하여 ciphertext $c_b$를 Alice에게 전달합니다.
- 2번 단계와 마찬가지로, Alice는 Decryption / Encryption Oracle을 사용하고 싶은만큼 사용할 수 있습니다. 단, $c_b$를 decrypt할 수는 없습니다.
- Alice는 $c_b$가 $m_{b’}$으로 부터 왔다는 guess $b’$를 Bob에게 전달합니다. $b=b’$인 경우 Alice가 이 게임을 승리합니다.
만약 Alice가 $\frac{1}{2}$보다 의미있게 높은 확률로 승리하는 것이 가능하다면 이는 Ciphertext indistinguishability가 깨진 것이므로 CCA2 공격이 성공했다고 볼 수 있습니다. 반대로, Alice가 $\frac{1}{2}$보다 의미있게 높은 확률로 승리할 수 없는 경우 Bob은 암호 시스템이 IND-CCA2 secure함을 증명한 것입니다.
위 예시에서 Alice가 Decryption Oracle을 이용할 수 없도록 한다면 이는 IND-CPA secure의 정의와 정확히 일치하게 됩니다.
IND-CPA secure하지 않은 대표적인 예시로는 textbook RSA를 들 수 있습니다. textbook RSA에서는 plaintext $m$에 대해 이에 대한 ciphertext $Enc_{pk}(m)$이 항상 동일하기 때문에, 5번 단계에서 encryption oracle을 사용하면 쉽게 올바른 b를 guess할 수 있습니다. 여기서 보듯이, Deterministic encryption scheme은 IND-CPA secure할 수 없습니다.
IND-CCA2 secure Symmetric Key Encryption
뒤에서 보겠지만, IND-CPA secure한 공개키 암호가 주어졌더라도 IND-CCA2 secure한 공개키 암호를 만들고 Ciphertext indistinguishability를 증명하는 것은 쉽지 않은 일입니다. 이에 비해, 대칭키 암호화(Symmetric Key Encryption)에서는 이 문제가 비교적 쉽게 해결됩니다.
대칭키 암호화는 공개키 암호화와 달리 암호화와 복호화에 사용되는 키가 동일하다는 특성이 있고, 대표적으로는 메시지를 동일한 크기의 블록으로 나누어 블록별로 키를 이용해 암호화하는 block cipher가 있습니다. block cipher의 예시로는 많은 곳에서 표준으로 지정되어 있는 AES block cipher와 이전에 많이 쓰였던 DES block cipher 등이 있습니다.
먼저, IND-CPA secure 대칭키 암호를 구성하는 방법에 대해 알아보겠습니다.
Theorem. length $k$의 key로 length $n$의 block을 encrypt하는 block cipher $F: (0,1)^{k} \times (0,1)^{n} \rightarrow (0,1)^{n}$ 가 pseudorandom permutation일 때, CTR Mode 또는 CBC Mode로 encrypt하는 경우 이 암호 시스템은 IND-CPA secure.
$(0,1)^{k}$는 $k$비트라는 의미에 적절하지 않은 표기법이지만, 이 블로그 형식에서 중괄호를 사용할 때 표시되지 않는 문제가 빈번히 발생하기 때문에 부득이하게 0 또는 1로 이루어진 길이 $k$의 bitstring들의 집합을 중괄호가 아닌 소괄호를 이용해 $(0,1)^k$로 표현하였습니다.
위에서 pseudorandom permutation의 정의는 Ciphertext indistinguishability의 정의와 상당히 유사한데, 어떤 polynomial-time distinguisher도 $F_{key}$와 random permutation $P: (0,1)^{n} \rightarrow (0,1)^{n}$를 구별하지 못한다는 의미입니다.
그러나 IND-CPA secure한 CTR Mode block cipher는 CCA2 attack에 취약할 수 있습니다. IND-CCA2 게임에서 Alice는 ciphertext $c_b$를 받은 후 $c_b \oplus 1$ 를 decrypt할 수 있고, 이로부터 $m_b \oplus 1$을 얻을 수 있으므로 $b$를 쉽게 guess할 수 있습니다.
이와 같은 공격이 가능한 근본적인 이유는 $Dec(c) = m$인 $c$가 주어졌을 때 이를 수정하여 $m$과 연관이 있는 $m’$로 복호화되는 ciphertext $c’$를 만드는 것이 가능하기 때문입니다(Malleability). 이를 방지하기 위해 message authentication code(MAC)를 이용할 수 있습니다. Decryption Oracle은 먼저 ciphertext의 MAC이 valid한지를 먼저 체크하고 그렇지 않으면 에러를 리턴할 것이므로, valid한 ciphertext를 만드는 난이도를 조절할 수 있게 됩니다. 즉, 공격자가 ciphertext를 만들었을 때 그것이 verify되어 성공적으로 decrypt될 확률이 0에 가깝도록 할 수 있습니다. 이러한 암호의 경우 공격자는 Decryption Oracle에서 decrypt가 정상적으로 되도록 쿼리를 하기 위해서는 plaintext를 만들고 그 encryption을 사용하는 방법밖에 없는 상황에 놓여 Decryption Oracle 자체가 큰 의미를 가지지 못하게 되어 버립니다.
Difference between Public Key Encryption
위 예시를 보면 공개키 암호에서도 동일하게 MAC을 넣으면 IND-CCA2 secure하도록 만들 수 있는 것이 아닌지 의문이 들 수 있습니다. 그러나, 대칭키 암호는 sender와 receiver는 대칭키를 공유하고 attacker는 모르는 상태인 반면 공개키 암호는 sender와 receiver도 서로의 secret key는 모르고, attacker에게도 자신의 public key/secret key 및 다른 사람들의 public key는 모두 알고 있는 상태라는 점이 다릅니다.
Encryption scheme에 추가적으로 공개키 암호 시스템에서 validity check를 위해 흔히 사용하는 digital signature(전자서명)을 붙여 암호화를 한다고 가정해봅시다. ciphertext $c = c0 + s$ 가 주어져있고 $s$가 signature라면 공격자는 $s$ 대신에 자신의 비밀키를 이용해 서명 $s’$를 생성해 $c’ = c0 + s’$에 대한 decryption 요청을 하여 $c$에 대한 plaintext를 얻을 수 있습니다. 즉, 키를 알고 있다라는 것에 기반한 authentication으로는 IND-CCA2 secure한 scheme을 만들 수 없습니다.
PKCS(Public-Key Cryptography Standards)#1 의 버전 1.5는 Chosen Ciphertext Attack에 대해 어느정도 고려하고 설계했더라도 secure하지 않을 수 있다는 좋은 예시를 보여줍니다. PKCS#1v1.5는 메시지에 random string을 붙임으로서 encryption을 deterministic하지 않게 만들어 IND-CPA secure 하도록 설계되었습니다. 또한 몇개의 check bit를 넣음으로써 임의로 생성한 ciphertext는 validity check를 통과하지 못하도록 하였습니다. 그러나 공격자는 ciphertext에 대한 verification의 성공/실패 여부를 알 수 있었고, 이 정보들을 이용해 ciphertext를 수정하여 check를 통과하는 또 다른 ciphertext를 만들 수 있었습니다. 결국 PKCS#1v1.5는 adaptive ciphertext attack이 가능함이 밝혀졌습니다(링크).
IND-CCA2 secure Public Key Encryption
앞에서 보았듯이, CCA2 공격이 가능한지 여부는 ciphertext를 변형하여 또 다른 valid ciphertext를 만들 수 있는지(malleable한지)에 의존하는 경우가 많습니다. Encryption이 malleable한 경우에 Chosen Ciphertext Attack은 너무 강력하고, 반대로 malleable하지 않다면 CCA는 결국 Encryption Oracle에서 이미 얻은 정보만을 Decryption Oracle에서 쓸 수 있기 때문에 CPA정도로 약해지게 됩니다. 지금부터는 malleable하지 않아서 IND-CCA2 secure한 Public Key Encryption scheme에 대해 알아볼 것입니다.
OAEP
PKCS#1은 앞서 v1.5에서 CCA2 attack이 가능함이 알려지고나서 버전 2에서는 이를 보완했는데, 이를 OAEP(Optimal Asymmetric Encryption Padding)-RSA 라고 합니다.
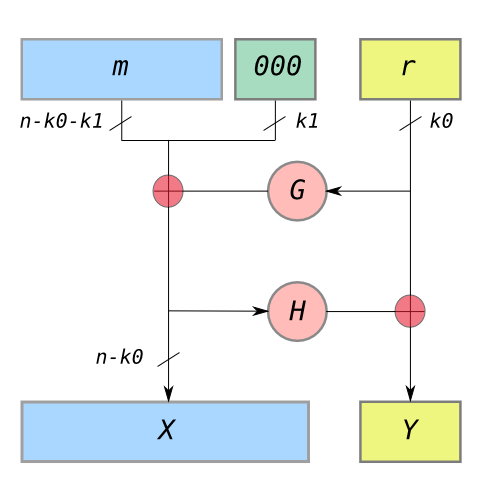
OAEP에서는 message $m$을 encryption 하기 전 padding 과정에서 마치 DES의 feistel network과 같은 과정을 거칩니다. RSA의 modulo $N$이 $n$비트의 수일때, 먼저 해시함수 $G: (0,1)^{k_0} \rightarrow (0,1)^{n-k_0}$와 $H: (0,1)^{n-k_0}\rightarrow (0,1)^{k_0}$을 준비하고, 길이 $k_0$의 random bitstring $r$을 고릅니다.
이때 $t = (m \mid \mid 0…0) \oplus G(r)$ 라 하면 최종적으로 encrypt될 값은 $padding(m) = t \mid \mid (H(t) \oplus r)$가 됩니다.
위 구조를 살펴보면 message $m$을 padding 과정을 계산하는 것은 매우 간단하고, 또한 역으로 $padding(m)$이 주어졌을 때 $m$을 복원하는 것도 $H(X) \oplus Y$와 $G(H(X) \oplus Y) \oplus X$를 계산하면 되는 간단한 과정임을 알 수 있습니다. 따라서, $m$ 이후의 $k_1$개의 비트가 0인지 체크하는 ciphertext valid check가 가능합니다. 한편, $G$와 $H$는 입력이 한 비트만 바뀌어도 모든 비트에 영향을 주는 Avalanche effect가 있는 hash function으로 가정되고, 이에 따라 padding(m)을 수정하여 validity check를 통과하도록 하는 것은 무작위로 생성했을때 통과하는 확률과 동일해집니다. 따라서, valid한 ciphertext를 만들기 위해서는 $k_1$의 길이에 exponential한 횟수의 oracle 사용이 필요하다고 볼 수 있습니다.
사실 위의 설명은 전혀 엄밀하지 않습니다. OAEP로 padding한 PKE가 IND-CCA2이기 위해서는 엄밀하게 $G$와 $H$는 random oracle이라는 가정이 필요합니다. 이는 $G$와 $H$가 완벽하게 random function임을 뜻합니다. 즉, 이때까지 입력으로 주어졌던 것 중 하나가 주어지면 그 때의 결과값이 나오지만, 그렇지 않은 경우 완전한 random function으로서 기능함을 의미합니다. random oracle은 매우 ideal한 가정으로 실제 사용하는 해시함수들은 random oracle이 아니지만, 안전함이 알려져있는 해시함수를 사용하는 경우 OAEP-RSA가 해시함수의 취약점이 발견되지 않는 가정하에 CCA2 attack으로부터 안전함이 보장되므로 의미가 있다고 할 수 있습니다.
Fujisaki-Okamoto Transform
Fujisaki-Okamoto Transform은 public-key encryption scheme $\Pi^{asy} = (Gen^{asy}, Enc_{pk}^{asy}, Dec_{sk}^{asy})$과 symmetric-key encryption scheme $\Pi^{sym} = (Gen^{sym}, Enc_{k}^{sym}, Dec_{k}^{sym})$이 주어져 있을 때 IND-CCA2 secure hybrid encryption을 만드는 일반적인 방법입니다. 여기에서 $Gen$은 키 생성 알고리즘, $Enc$는 암호화 알고리즘, $Dec$는 복호화 알고리즘을 의미합니다.
Fujisaki-Okamoto Transform에 대해 소개하기 전에, 먼저 간단하게 생각할 수 있는 hybrid encryption scheme에 대해 알아봅시다.
Hybrid encryption Scheme. public-key encryption scheme $\Pi^{asy}$의 message space $M$이 symmetric-key encryption scheme $\Pi^{sym}$의 key space와 같을 때, 다음과 같은 Hybrid encryption Scheme $\Pi^{hyb} = (Gen^{hyb}, Enc_{pk}^{hyb}, Dec_{sk}^{hyb})$를 만들 수 있습니다.
$Gen^{hyb}$ : PKE의 키 생성 알고리즘을 그대로 사용하여 $pk, sk$를 생성합니다.
$Enc_{pk}^{hyb}$: 메시지 $m$을 암호화할 때는 먼저 $M$에서 랜덤하게 $k$를 고른 후, $Enc_{pk}^{asy} = c_k$와 $Enc_{k}^{sym}(m) = c_m$을 만들어 $Enc_{pk}^{hyb}(m) = c_m \mid \mid c_k$ 로 둡니다.
$Dec_{sk}^{hyb}$: $c$를 decrypt할 때는 먼저 $c$를 $c_m$과 $c_k$로 분리하고, $Dec_{sk}^{asy}(c_k) = k’$를 구해 $k’ \in M$인지 validity check를 합니다. 이를 통과했다면 $m’ = Dec_{k’}^{sym}(c_m)$으로 decrypt를 완료합니다.
PKE $\Pi^{asy}$가 IND-CPA secure한 경우, SKE $\Pi^{sym}$가 Ciphertext only attack에만 secure해도 Hybrid encryption scheme이 IND-CPA secure임이 증명되어 있습니다. 그러나, 둘 모두 IND-CPA secure 인 경우라도 $\Pi^{hyb}$가 IND-CCA2 secure하게 되지는 않습니다.
Fujisaki-Okamoto Scheme. PKE scheme $\Pi^{asy}$과 SKE scheme $\Pi^{sym}$이 주어졌을 때, random oracle $G, H$ 를 기반으로 Fujisaki-Okamoto Scheme $\Pi^{fo} = (Gen^{fo}, Enc_{pk}^{fo}, Dec_{sk}^{fo})$를 만들 수 있습니다.
$Gen^{fo}$ : PKE의 키 생성 알고리즘을 그대로 사용하여 $pk, sk$를 생성합니다.
$Enc_{pk}^{fo}$: $m$을 암호화하는 과정은 아래의 과정을 거칩니다.
- 랜덤하게 $\Pi^{asy}$의 message $r$을 고릅니다.
- $k = G(r)$
- $c_m \leftarrow Enc_{k}^{sym}(m)$
- $h = H(r, c_m)$
- $c_r = Enc_{pk}^{asy}(r; h)$
- $Enc_{pk}^{fo}(m) = c_m \mid \mid c_r$ 로 둡니다.
위 과정에서 3번과 5번, 특히 5번에 대해 notation이 이해가 가지 않을 것입니다. 먼저 3번에서 encryption에 대입 대신 $\leftarrow$가 들어간 이유는 Encryption이 deterministic하지 않을 수 있기 때문에 $c_m$이 가능한 결과값 중 랜덤으로 선택된다는 뜻입니다.
5번의 $Enc_{pk}^{asy}(r; h)$ 에서 $h$는 randomness parameter으로, $Enc_{pk}$는 원래 deterministic encryption이 아닌 probabilistic encryption일 수 있지만, 이를 randomness parameter를 추가적으로 받는 것으로 생각하여 given randomness parameter에서는 deterministic으로 생각하는 것입니다. 즉, $Enc_{pk}^{asy}(r; h)$의 값은 항상 하나로 정해집니다. 이처럼 randomized encryption을 deterministic encryption과 randomness parameter로 분리하여 생각하는 것은 Fujisaki-Okamoto transform의 핵심적인 부분입니다.
$Dec_{sk}^{fo}$: $c$의 decryption은 아래의 과정을 거칩니다.
- $c$를 $c_m$과 $c_r$로 파싱합니다.
- $r’ = Dec_{sk}^{asy}(c_r)$
- $r’$이 $\Pi^{asy}$의 message space에 포함되지 않을경우 에러를 리턴합니다.
- $h’ = H(r’, c_m)$
- $c_r’ = Enc_{pk}^{asy}(r’; h’)$
- $c_r \neq c_r’$이면 에러를 리턴합니다.
- $k’ = G(r’)$
- $Dec_{sk}^{fo}(c) = Dec_{k’}^{sym}(c_m)$
Fujisaki-Okamoto Scheme이 올바르게 작동하는 scheme임은 쉽게 확인할 수 있습니다.
Theorem. PKE $\Pi^{asy}$가 IND-CPA secure하고, SKE $\Pi^{sym}$가 Ciphertext only attack에 secure한 경우, Fujisaki-Okamoto Scheme $\Pi^{fo}$는 IND-CCA2 secure합니다.
간단히 살펴보면 Fujisaki-Okamoto Scheme은 OAEP와 마찬가지로 random oracle을 가지고 있기 때문에 c_m과 c_r 중 어떤 것을 변형해도 decryption의 3, 6번 스텝의 validity check를 통과하는 것이 사실상 불가능함이 보장되어 Non-Malleability와 PKE의 IND-CPA secureness로 IND-CCA2가 보장된다고 생각할 수 있습니다.
엄밀한 증명의 경우 IND-CCA2에 대한 game $G_0$을 여러 단계의 reduction을 통해 다른 game으로 변형하여 공격자의 승리 확률이 $\frac{1}{2} + \epsilon$을 넘을 수 없음을 보이는 방식으로 증명이 가능합니다. 간단히 살펴보면
- $G_0$ 은 위에서 우리가 살펴본 게임과 동일합니다. 공격자 alice는 Decryption 및 random oracle $G, H$ 를 자유롭게 호출할 수 있습니다.
- $G_1$은 $G_0$과 다른 것은 모두 동일하고, random oracle $G, H$에 대한 결과를 Bob이 답하는 게임입니다. 단 $G, H$에 대해 이미 동일한 질문이 이전에 왔다면 동일한 결과를 돌려주어야 합니다.
- $G_2$는 $G_1$에서 secret key $sk$가 필요하지 않은 새로운 decryption oracle을 만듭니다. 이 decryption oracle은 현재까지 random oracle $H$에 대해 질문한 쌍 중에 $H(r’, c_m) = h’$이 존재하여 $c_r = Enc_{pk}^{asy}(r’; h’)$을 만족하는 경우에만 $Dec_{G(r’)}^{sym}(c_m)$을 리턴하고 이외에는 에러를 리턴합니다.
- $G_3$은 ciphertext를 만들 때 random oracle을 사용하지 않는 점을 빼면 $G_2$와 동일합니다. encryption의 2번 스텝인 $k = G(r)$는 SKE의 key space에서 random sample하는 것으로 대체되고, $h = H(r, c_m)$ 도 PKE의 randomness parameter space에서 sample하는 것으로 대체됩니다.
$S_i$를 $G_i$에서 attacker가 승리하는 event라고 했을 때, $Pr[S_3]$의 upper bound를 구하고, $Pr[S_{i+1}] - Pr[S_i]$를 bound시켜서 결국 $Pr[S_0]$를 $\frac{1}{2} + \epsilon$으로 bound시킬 수 있음을 보이는 것이 IND-CCA2 증명의 개요입니다.
Fujisaki-Okamoto Transformation은 여러가지 변형이 있으며, 처음에 나왔을 때에 비해 발전된 scheme도 발견되었습니다. 발전된 scheme 및 post-quantum setting에서의 분석은 이 논문 에서 보다 잘 확인할 수 있습니다. FO transform은 post-quantum setting에서도 CCA 공격으로부터 안전한 것으로 알려져 있습니다.
참고 자료
- https://cs.uni-paderborn.de/fileadmin/informatik/fg/cuk/Lehre/Abschlussarbeiten/Bachelorarbeiten/2014/BA_Lippert_FOT_final.pdf
- https://en.wikipedia.org/wiki/Block_cipher_mode_of_operation
- https://en.wikipedia.org/wiki/Optimal_asymmetric_encryption_padding
- https://blog.cryptographyengineering.com/2018/07/
- https://en.wikipedia.org/wiki/Ciphertext_indistinguishability