ESPiRiT을 이용한 Sensitivity Computation

Introduction

지난 글에서는 MRI의 개괄적인 원리, 즉 장비에서 얻은 raw data를 어떻게 이미지로 변환하는지에 대해 다루어보았습니다. 또한 그 중에서 scan time을 줄이기 위한 기법인 Parallel imaging과, 그로 인한 이미지 퀄리티 저하를 보상하는 알고리즘 중 SENSE, GRAPPA, 그리고 PRUNO에 대해 간략히 다루었습니다.

현재 가장 두루 쓰이는 방법은 GRAPPA, SENSE이지만 이 둘은 벌써 고안된 지 20년이 넘어가는 classic한 알고리즘입니다. Practical하진 않지만, 연구나 다른 특수한 목적으로 개발된 고성능 알고리즘들이 쏟아져나왔죠. 오늘은 그 중에서 수학적으로도 흥미롭고, 꽤 재미있는 인사이트를 주는 ESPiRiT (Uecker, 2014)의 원리와 의의, 구현법에 대해 알아봅니다.

Impact of Coil Sensitivity in MRI reconstruction

이 장의 이미지 출처는 Hamilton et al, 2017임을 밝힙니다.

MRI 장비에서는 인체 속 수소 원자가 방출하는 RadioFrequency Pulse, 즉 전자기 신호를 감지합니다. 이는 환자를 에워싸는 코일들에게 감지되는데, 당연히 코일마다 신호 source의 위치에 따라 감지하는 신호의 세기가 다릅니다.

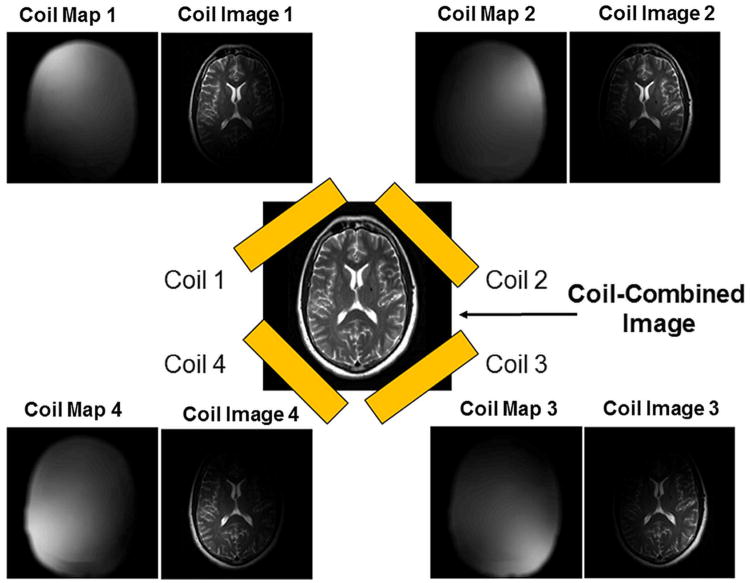
이미지: Hamilton, 2017

사람의 뇌에서 나오는 신호의 세기가 가운데 그림과 같다면, 각 코일에선 “Coil Sensitivity” (그림의 Coil Map) 라는 가중치가 곱해진 이미지를 얻게 됩니다. 대개 코일의 위치에서 가까운 부분의 신호를 더 잘 감지하는 것을 볼 수 있습니다.

가운데 사진과 같이 완전한 이미지를 얻기 위해서는 각 코일에서 얻은 이미지를 합성해야 합니다. 이 과정을 Coil-Combine이라고 하는데, 대개는 아래의 Sensitivity combine을 사용합니다.

\[m(\mathbf{r}) = \frac{\sum _ {c} S _ {c}(\mathbf{r})^{*} x _ {c}(\mathbf{r})}{\sum _ {c} \left\lvert S _ {c}(\mathbf{r}) \right\rvert^{2}}\]
$S _ {c}(\mathbf{r})$은 $c$번째 코일의 위치 $\mathbf{r} = (x, y, z)$에서의 Sensitivity, $x _ {c}(\mathbf{r})$은 $c$번째 코일이 감지한 위치 $\mathbf{r}$의 신호.

Sensitivity를 알 수 없는 경우, 아래의 RSS (Root-Sum-Square) Combine을 대신 사용하기도 합니다.

\[m _ {\mathrm{RSS}}(\mathbf{r}) = \sqrt{\sum _ {c} \left\lvert x _ {c}(\mathbf{r}) \right\rvert^{2}}\]

두 방법은 $x _ {c}(\mathbf{r}) = S _ {c}(\mathbf{r})m(\mathbf{r})$, $\sum _ {c} \left\lvert S _ {c}(\mathbf{r})\right\rvert^{2} = 1$이 성립하는 ideal case에서 동등합니다. 하지만 $x _ {c}$에 noise가 있는 경우, $S$가 normalize되어 있지 않은 경우에는 Signal-to-noise ratio (SNR) 측면에서 전자가 더 좋은 방법입니다. 즉 Sensitivity를 알고 있는 경우에는 그렇지 않은 경우보다 질 높은 이미지를 만들 수 있는 것입니다. Coil combine과 같은 상황만이 아니라, Parallel imaging 등으로 이미지 퀄리티가 낮아진 상황에서도 Sensitivity Map은 큰 도움이 됩니다.

아래 두 식은 유명한 Parallel imaging technique에 Sensitivity map $S$가 사용되는 예시입니다.

SENSE (Pruessman, 1999) $m = \left(S^{\mathrm{H}}\Psi^{-1} S + \lambda^{-1}\right)^{-1} S^{\mathrm{H}} \Psi^{-1}P$ $\ell _ {1}$-SPiRiT (Lustig, 2007) $m = \arg\min _ {x} \left( \left\lVert y - \mathcal{UF}Sm \right\rVert _ {2}^{2} + \lambda \left\lVert \Psi m \right\rVert _ {1} \right)$

Low frequency of Coil Sensitivity maps

Coil Sensitivity는 비교적 간단한 물리 법칙을 따르기 때문에, 공간에 따른 분포가 상당히 smooth하다는 점에서 계산이 꽤 용이하다는 장점이 있습니다. 다시 말해, 이를 k-space (Fourier domain) 상에서 나타냈을 때 high frequency 영역이 나타나지 않습니다.

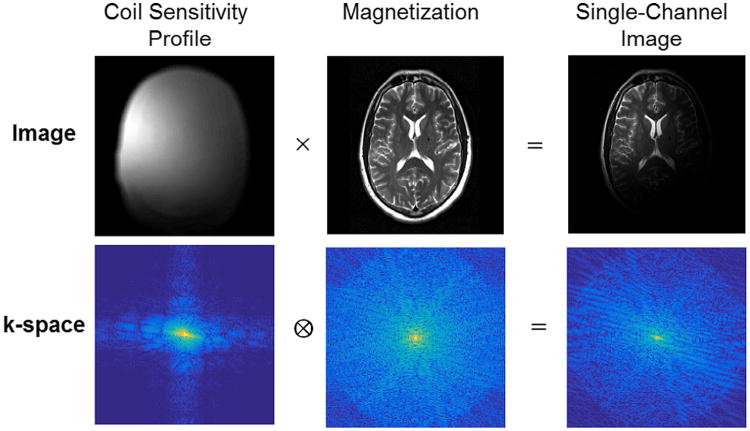
k-space diagram of sensitivity and magnetization

이미지 사이의 point-wise 곱은 k-space 상에서 convolution이 됩니다. 때문에 각 코일에서 얻어진 k-space signal은 “ground-truth k-space signal”에 coil sensitivity를 convolve한 것으로 볼 수 있는데, 많은 모형에서 coil-sensitivity를 small width convolution kernel로 가정합니다. 이미지 resolution이 256-1024인데 반해 보통 sensitivity convolution kernel의 크기는 10을 넘기지 않습니다.

Autocalibrating sensitivity maps

이미지만 보고 Sensitivity map을 알 수 있다면 좋겠지만, 그리 간단한 일이 아니기 때문에 보통은 Sensitivity map을 따로 측정하는 방법을 사용합니다. 하지만 이 과정에서 frame의 움직임, 코일의 측정 오류 등 여러 artifact가 누적되어 부정확한 결과를 가져올 수 있고, 때로는 Sensitivity 데이터를 사용하지 못하는 상황도 있습니다.

하지만 그리 간단하지 않은 일을 거의 처음으로 해내다시피 한 결과가 바로 오늘 리뷰할 논문인 ESPiRiT으로, 오직 k-space data를 사용하여 Sensitivity map을 eigenvector로 갖는 matrix $\mathcal{W}$를 설계하였습니다. 이렇게 얻으면 Sensitivity map을 별도로 측정하는 과정에서 생기는 여러 문제점을 회피할 수 있고, Sensitivity map을 사용하는 여러 고성능 Parallel imaging algorithm의 장점 또한 누릴 수 있습니다.

ESPiRiT – exploiting local correlation of k-space

다음과 같은 convention을 가정합시다.

이미지와 k-space는 모두 2차원. 다만 모든 논의는 3차원으로 자연스럽게 확장할 수 있습니다.
Convolution kernel에서 중심점의 좌표는 항상 $\mathbf{0}$. width가 $2A+1$인 kernel $K$에 대해 $(K \ast X)(r) = \sum _ {x = -A}^{A} K(x)X(r - x)$ . (단, $\ast$ 는 convolution operator)

Local Linear Dependence of k-space

k-space위의 한 점 $\mathbf{k}$를 생각하고, $\mathbf{k}$ 를 중심으로 하는 한 변의 길이가 $w _ {d}$인 정사각형을 그려봅시다. 편의상 k-space가 2d이고 코일이 $C$개라고 가정하면, k-space data point는 총 $Cw _ {d}^{2}$개가 모일 것입니다. 각 코일의 Sensitivity map kernel의 크기가 $w _ {s}$라고 하면, 실제로 이 $Cw _ {d}^{2}$개의 점은 $(w _ {d} + w _ {s} - 1)^{2}$개의 magnetization data로 생성된 셈입니다. $C \gg 1$이므로 $w _ {d}$가 충분히 크다면, 이 점들 사이에 $\mathbf{k}$에 의존하지 않는 linear correlation이 생기게 될 것입니다. 이를 k-space의 local linear dependence라고 합니다.

GRAPPA (Griswold, 2002)는 이러한 linear correlation을 아주 잘 파고든 알고리즘입니다. 다음과 같은 $C \times C$ kernel $G$의 존재를 가정하는 것이죠. (여기서 $A \times B$ kernel이란 input channel이 $B$개이고 output channel이 $A$개인 convolution kernel을 의미하며 width가 $A \times B$라는 말과는 다릅니다)

$G _ {c, d}(\mathbf{0}) = -\delta _ {cd}$

For k-space $X$, $G \ast X =0$ in every point of k-space.

Width of $G$ (2 - 5) is way smaller than the width of $X$.

만약 parallel imaging으로 인해 어떤 point $\mathbf{r}$이 없어졌다면, Grappa kernel $G$의 도움을 받아 k-space point $X _ {c}(\mathbf{r})$을 복원할 수 있습니다.

\[0 = (G \ast X) _ {c}(\mathbf{r}) = -X _ {c}(\mathbf{r}) + \sum _ {\mathbf{s} \neq \mathbf{0}, d} G _ {cd}(\mathbf{s})X _ {d}(\mathbf{r - s})\]

이러한 $G$를 least-square method로 fitting하는 것이 grappa algorithm의 틀이라고 볼 수 있습니.

Fully Enjoying the null-space of $X$

ESPiRiT이나 PRUNO와 같은 method들은 GRAPPA에 비해 local linear correlation을 보다 유연하게 활용합니다. 이를 위해, “local linear correlation”을 보다 정확하게 정의해봅시다.

k-space의 각 점 $\mathbf{k}$에 대해, $\mathbf{k}$를 중심으로 $w _ {d} \times w _ {d}$ 정사각형 내에 위치한 $Cw _ {d}^{2}$개의 점들을 하나의 row vector로 나타냅시다. Local Linear Correlation을 구할 sample point가 $B$개 존재한다고 하면, 우리는 거대한 $B \times Cw _ {d}^{2}$ 크기의 tall matrix를 얻을 수 있습니다. 이렇게 만든 행렬을 block hankel matrix라고 부릅니다.

block hankel matrix $A$의 입장에서 local linear correlation이 있다는 말은 곧 $A$의 column rank가 낮다는 것을 의미합니다. 따라서 $A$를 span space와 null space로 구분하면 모든 correlation을 얻을 수 있을 것입니다. 이는 보통 $A$에 SVD(Singular Value Decomposition)를 적용하여 cutoff singular value $\sigma _ {0}$보다 singular value가 큰 singular vector를 span space로, 작은 singular vector를 null-space로 보내는 것으로 구분합니다.

Formulating flexibilized local correlations

$A$의 singular vector 중 span space로 분류된 것을 $V _ {\Vert}$, null space로 분류된 것을 $V _ {\perp}$라고 둡시다. $V _ {\perp}$는 hankel matrix에 대한 eigenvector(정확히는 singular vector)로도 볼 수 있지만, Hankel matrix의 정의를 생각해보면 그 본질은 convolution kernel입니다. $V _ {\perp}$의 matrix size가 $Cw _ {d}^{2} \times U$라고 두면, $V _ {\perp}$를 $U \times C$ convolution kernel로 볼 수 있는 것입니다. Nulling kernel의 본질에 따라 $V _ {\perp} \ast X = 0$이라는 convolution-style의 관계식이 얻어지지만, concise한 식 전개를 위해 조금 더 hankel matrix 위에서 논리를 전개해봅시다.

$X$를 길이가 $CN _ {x}N _ {y}$인 거대한 벡터로 생각하는 대신 “Extraction operator” $R _ {\mathbf{k}}$를 정의하여, $R _ {\mathbf{k}}X$가 $\mathbf{k}$를 중심으로 하는 길이 $Cw _ {d}^{2}$짜리 벡터가 되도록 합시다. 즉, 기존에 만든 hankel matrix $A$는 Sampling location이 $\mathbf{k} _ {1}, \cdots, \mathbf{k} _ {B}$라면 $A = \begin{bmatrix} R _ {\mathbf{k} _ {1}} X & \cdots & R _ {\mathbf{k} _ {B}} X \end{bmatrix}^{\mathrm{H}}$가 되는 셈입니다. 이 notation을 도입하면

$V _ {\perp} \ast X = 0 \implies V _ {\perp}^{\mathrm{H}} R _ {\mathbf{k}}X = 0 \;\forall \mathbf{k}.$

로 linear-algebra style 관계식을 쓸 수 있습니다. 좌변의 $V _ {\perp}$는 kernel, 우변의 $V _ {\perp}$는 matrix임에 주의하세요. 위 식의 우변을 positive semidefinite form으로 적고, 모든 $\mathbf{k}$에 대해 더하면 아래와 같은 식을 얻습니다.

\[\sum _ {\mathbf{k}} R _ {\mathbf{k}}^{\mathrm{H}} V _ {\perp} V _ {\perp}^{\mathrm{H}} R _ {\mathbf{k}} X = 0.\]

SVD의 orthonormality에 따라 $V _ {\perp}V _ {\perp}^{\mathrm{H}} + V _ {\Vert}V _ {\Vert}^{\mathrm{H}} = I$이므로, $\sum _ {\mathbf{k}} R _ {\mathbf{k}}^{\mathrm{H}}(V _ {\Vert}V _ {\Vert}^{\mathrm{H}})R _ {\mathbf{k}} X = \sum _ {\mathbf{k}} R _ {\mathbf{k}}^{\mathrm{H}}R _ {\mathbf{k}} X$ 이 때 $\sum _ {\mathbf{k}} R _ {\mathbf{k}}^{\mathrm{H}}R _ {\mathbf{k}}$는 정확히 $Cw _ {d}^{2} \cdot I$가 됨을 알 수 있습니다. (with periodic boundary condition on k-space) $M = Cw _ {d}^{2}$로 두면, 아래 관계식이 유도됩니다. $\left(\frac{1}{M}\sum _ {\mathbf{k}} R _ {\mathbf{k}}^{\mathrm{H}}V _ {\Vert}V _ {\Vert}^{\mathrm{H}}R _ {\mathbf{k}}\right) X = X$ 이 때 좌변에 가해진 operator $\left(\frac{1}{M}\sum _ {\mathbf{k}} R _ {\mathbf{k}}^{\mathrm{H}}V _ {\Vert}V _ {\Vert}^{\mathrm{H}}R _ {\mathbf{k}}\right)$를 $\mathcal{W}$라고 두면, $\mathcal{W}X = X$를 만족하므로 $X$는 $\mathcal{W}$의 eigenvector (with eigenvalue $1$)이 됨을 알 수 있습니다.

The “ESPiRiT operator” $\mathcal{W}$

$\mathcal{W}$를 보고 첫눈에 알아챌 수 있는 성질은 $\mathcal{W}$가 Positive semidefinite, hermitian operator라는 것입니다. 따라서 모르긴 몰라도 Eigenvector를 구하는 과정이 쉬울 것 같습니다.

차근차근 뜯어보면 알 수 있는 성질은 $\mathcal{W}$의 eigenvalue가 $1$ 이하라는 것입니다. SVD의 orthonormality에 의해 $V _ {\Vert}V _ {\Vert}^{\mathrm{H}}$가 projection operator가 되어 eigenvalue가 1이하가 되고, 한 k-space position $\mathbf{k}$에 대해 정확히 $M$개의 summand가 영향을 주기 때문입니다. 따라서 $X$는 단순히 “특정 고윳값을 갖는 eigenvector” 정도가 아니라 “maximum eigenvector”가 됩니다.

$V _ {\perp}$ (나아가 $V _ {\Vert}$)를 convolution operator로 볼 수 있듯이, $\mathcal{W}$ 또한 convolution kernel로 볼 수 있습니다. 구체적으로 $\mathcal{W}$는 $C \times C$ kernel이 되는데, 직관적으로 알 수 있는 사실이니 식을 찬찬히 들여다보고 유도해보시기 바랍니다.

Key theorem: Point-wise decomposition of $\mathcal{W}$

MRI에서 가장 중요한 식 중 하나인 Signal equation을 복기해보면 다음과 같습니다.

$X _ {c}(\mathbf{k}) = \sum _ {\mathbf{r}} \omega^{-\mathbf{r} \cdot \mathbf{k}} S _ {c}(\mathbf{r})m(\mathbf{r}) = \mathcal{F} \left\lbrace S _ {c} \odot m \right\rbrace(\mathbf{k})$

$\odot$은 element-wise product를 matrix multiplication과 구분하기 위한 표기이고, $\mathcal{F}$는 discrete fourier transform입니다. 이 식을 Eigenvalue equation $\mathcal{W}X = X$에 끼워넣으면 $\left(\mathcal{F}^{-1}\mathcal{W}\mathcal{F}\right)(S _ {c} \odot m) = S _ {c} \odot m$ 이 됩니다. 따라서 Operator $\mathcal{G} = \mathcal{F}^{-1}\mathcal{W}\mathcal{F}$이 상당히 궁금해지는데, 꽤 비직관적인 아래 사실이 성립합니다.

$\mathcal W$는 convolution이기때문에 $\tilde{\mathcal W} := \mathcal F^{-1} \mathcal W \mathcal F$ 는 pointwise matrix operation으로 분리 된다: $\tilde{\mathcal W}\big\vert _ {q} = \mathcal G _ q = G _ q^H G _ q$.

이것이 사실이라고 한다면, $\mathcal{G} _ {q}$는 점을 고정한 채 convolution channel끼리만 mixing하는 $C \times C$ positive semidefinite matrix가 되고, $\mathcal{G}$는 batch matrix multiplication이 됩니다. 따라서 거대한 크기의 matrix $\mathcal{W}$와 씨름할 필요 없이 각 점 $\mathbf{q}$마다 $\mathcal{G} _ {q}S _ {c}(\mathbf{q})m(\mathbf{q}) = S _ {c}(\mathbf{q})m(\mathbf{q})$를 해결하면 되고, $m(\mathbf{q}) \neq 0$ 조건에서 길이 $C$짜리 벡터 $S _ {\cdot}(\mathbf{q})$는 $\mathcal{G} _ {q}$의 maximum eigenvector가 됩니다.

Proof of Key theorem

결국 다음과 같은 명제를 증명하면 됩니다.

$K$가 $C \times C$ convolution이면, $\mathcal{F}^{-1}K\mathcal{F}$는 batch of $C \times C$ matrix multiplication이 된다.

$K$가 positive semidefinite이라면 $\mathcal{F}^{-1}K\mathcal{F}$ 역시 PSD인 것은 자명하기 때문에 $\mathcal{G} _ {q} = G _ {q}^{\mathrm{H}}G _ {q}$는 추가로 증명할 필요가 없습니다.

$Y = K \ast X$라는 convolution 관계식에서 $Y = \mathcal{F}y, X = \mathcal{F}x, K = \mathcal{F}L$이라고 두면 우리는 $\mathcal{F}^{-1}K\mathcal{F}x = y$가 $x, L$에 대한 식으로 어떻게 쓰이는지 보면 됩니다. $\begin{aligned} y _ {c}(\mathbf{r}) &= \sum _ {\mathbf{k}} Y _ {c}(\mathbf{k}) \omega^{\mathbf{r} \cdot \mathbf{k}}\\ &= \sum _ {\mathbf{k,l},d} K _ {cd}(\mathbf{l})X _ {d}(\mathbf{k - l})\omega^{\mathbf{r} \cdot \mathbf{k}}\\ &= \sum _ {\mathbf{k, l, u, v}, d} L _ {cd}(\mathbf{u})x _ {d}(\mathbf{v}) \omega^{\mathbf{r \cdot k -u \cdot l - v \cdot (k - l)}}\\ &= \sum _ {\mathbf{u,v},d} L _ {cd}(\mathbf{u})x _ {d}(\mathbf{v}) \delta _ {\mathbf{r, v}}\delta _ {\mathbf{r, u}}\\ &= \sum _ {d} L _ {cd}(\mathbf{r})x _ {d}(\mathbf{r})\quad \square \end{aligned}$

Exercise. $G _ {q}$가 사실은 $V _ {\Vert}$의 Fourier transform이 됩니다. $\mathcal{W}$의 식으로부터 이를 유도하세요.

Computation of ESPiRiT

위의 복잡한 과정으로 Sensitivity map을 구하고 나면, 구한 Sensitivity map을 SENSE, SPiRiT 등의 알고리즘에 꽂아넣는 것으로 undersampled k-space를 채울 수 있습니다. SPiRiT은 일종의 Compressive Sensing 알고리즘으로, 이 글에서 대략적인 원리를 공부할 수 있습니다.

ESPiRiT은 BART 그룹의 리더 Uecker가 만든 알고리즘이다보니, 저자가 구현한 C 기반 코드가 깃허브에 공개되어 있습니다. Sensitivity map을 만들기 위한 computational task를 간단히 아래와 같이 나눌 수 있습니다.

Block Hankel matrix $A$를 만들고, $A$의 SVD로 부터 $V _ {\Vert}$와 $V _ {\perp}$를 만들기.
$V _ {\Vert}$의 Fourier transform으로 $G _ {q}$를 만들기
$G _ {q}$ ($C \times C$행렬, 총 $N _ {x}N _ {y}$개의 batch) matrix의 maximum singular vector 찾기.
- 이미지 퀄리티를 위해 maximum singular vector가 아닌, 가장 큰 $k \approx 4$개의 maximum singular vector를 찾아야 하는 경우가 있음.

이 중 첫 번째 SVD는 그다지 시간을 요구하지 않습니다. 다만 $G _ {q}$ matrix가 최대 $C \times (Cw _ {d}^{2} - U) \times N _ {x}N _ {y}$ 까지 커질 수 있고, $\mathcal{G} _ {q} = G _ {q}^{H}G _ {q}$가 $C \times C \times N _ {x}N _ {y}$ 크기의 batch of matrices가 되는 것이 부담이라면 부담입니다. 또한 각 행렬마다 $\mathcal{O}(C^{3})$ 시간이 소요되는 SVD를 사용하는 것이 많은 시간을 소모하기도 합니다. 이를 위한 좋은 대책은

CUDA 기반의 라이브러리로 빠른 batch svd를 사용하기.
가장 큰 $k$개의 eigenvector를 찾기 위해 SVD 대신 Power iteration (혹은 그 일반화인 Orthogonal iteration) 구현하기

등이 있습니다. BART는 수 년간 코드베이스를 관리하며 이러한 최적화들을 적용해왔지만, 제가 확인했을 때 아직 최적화할 부분이 많이 남아있습니다. C나 CUDA를 이용한 오픈 소스 contribution을 원하시고, 이러한 task에 관심이 있다면 연락 주시기 바랍니다.

Reference

ESPiRiT: Uecker, M., Lai, P., Murphy, M. J., Virtue, P., Elad, M., Pauly, J. M., Vasanawala, S. S., & Lustig, M. (2014). ESPIRiT–an eigenvalue approach to autocalibrating parallel MRI: where SENSE meets GRAPPA. Magnetic resonance in medicine, 71(3), 990–1001. https://doi.org/10.1002/mrm.24751

SENSE: Pruessmann KP, Weiger M, Scheidegger MB, Boesiger P. SENSE: sensitivity encoding for fast MRI. Magn Reson Med. 1999 Nov;42(5):952-62. PMID: 10542355.

GRAPPA: Griswold MA, Jakob PM, Heidemann RM, Nittka M, Jellus V, Wang J, Kiefer B, Haase A. Generalized autocalibrating partially parallel acquisitions (GRAPPA). Magn Reson Med. 2002 Jun;47(6):1202-10. doi: 10.1002/mrm.10171. PMID: 12111967.

JSENSE: Ying L, Sheng J. Joint image reconstruction and sensitivity estimation in SENSE (JSENSE). Magn Reson Med. 2007 Jun;57(6):1196-202. doi: 10.1002/mrm.21245. PMID: 17534910.

SENSE의 결점: FOV가 작을 때: Griswold MA, Kannengiesser S, Heidemann RM, Wang J, Jakob PM. Field-of-view limitations in parallel imaging. Magn Reson Med. 2004 Nov;52(5):1118-26. doi: 10.1002/mrm.20249. PMID: 15508164.