알고리즘 문제 접근 과정 7
알고리즘 문제 접근 과정 7
이번 포스트에서도 ‘알고리즘 문제 접근 방법’ 시리즈에서 진행했듯이 특정 문제를 해결하기 위해 가장 낮은 단계의 접근에서부터 최종 해법까지 해결해나가는 과정을 작성합니다.
최대한 다양한 유형의 문제들을 다루어, 많은 문제 유형에서의 접근 방법에 대한 실마리를 드리는 역할을 하려 합니다.
방 청소 - COCI 2013/2014 Contest #5 6번
풀이
문제 상황이 단순하지 않아서, 어떻게 풀지 쉽게 감이 오지 않을 수 있습니다. 한 음료를 담을 수 있는 상자는 두 개뿐이지만, 음료를 어떻게든 옮겨서 담을 수 있다면 그 상태를 만들어 담아내기 때문에 현 상태가 i개의 음료를 모두 담을 수 있는 상황인지 판단하기는 꽤나 쉽지 않습니다.
일단 가장 단순하게 생각한다면, 각 단계마다 모든 술을 각각 A, 혹은 B 상자에 담아보면서 겹치는지 아닌지 확인하는 방법이 있습니다. 이 방식으로 문제를 풀 경우 $O(N * 2^N)$에 문제를 풀 수 있습니다만, N이 굉장히 클 수 있는 이 문제를 풀기엔 적합하지 않습니다.
그렇다면, 어떻게 문제를 쉽게 생각할 수 있을까요?
이를 위해서는 먼저 규칙을 천천히 살펴볼 필요가 있습니다.
1번부터 5번규칙까지 읽으면, 결국 우리는 담을 수 있는 상태가 하나라도 있다면 그 방식대로 음료를 옮겨담는 것으로 문제를 해결할 수 있다는 것을 알 수 있습니다. 이를 위해 현재의 상태를 A, 다음 음료를 담는 상태를 B라고 합시다. 그리고 이 때, A와 B가 어떻게 구성되는지 살펴봅시다.
- 상자 c가 A에서 쓰이지만, B에선 쓰이지 않는 경우
이 경우 B 상태에서는 c에 담기지 않았지만, c에 담을 수 있는 음료가 항상 존재하기 때문에 그 음료를 c에 담는 것으로 같게 만들 수 있습니다.
B와 A 상태의 음료는 항상 하나 차이이며, A에서의 음료는 B 상태에서도 항상 존재하기 때문에 우리는 언제나 A에 쓰인 상자들을 쓰도록 B를 만들 수 있습니다. 그렇다면, 더 담아야하는 음료는 항상 하나가 존재하게 되는데, 그 경우는 다음과 같습니다.
- 상자 c가 A에서 쓰이지 않지만, B에선 쓰이는 경우
이러한 상자 c는 항상 두 가지 경우만이 있을 수 있습니다. 새로운 음료가 c에 들어가거나, 혹은 새로운 음료가 원래 있던 상자들의 음료를 밀어낸 이후 A에 존재하던 음료가 c로 들어가는 경우만이 존재합니다.
즉, 어떠한 상태에서든 항상 새 음료를 넣어서 새로운 최적의 상태를 만들 수 있다는 것을 알 수 있고, 우리는 특별히 다른 것을 고려하지 않고 항상 새로 쓰일 상자가 무엇인지만 찾아내면 됩니다.
그렇다면, 새로 쓰일 수 있는 상자의 존재 여부는 어떻게 알아낼 수 있을까요?
한 음료수는 항상 두 개의 상자에 넣을 수 있습니다. 이 때, 상자에 들어가있는 음료는 항상 두 가지의 상태로만 있을 수 있습니다.
- 현재 들어가 있는 상자와 다른쪽 상자 모두 차있는 경우
- 다른쪽 상자가 비어있는 경우
이 때, 상자에 들어가있는 음료는 A나 B 둘 중 하나의 상자에 들어가있으므로, 항상 옮길 수 있다면 최대 하나의 상자로만 옮겨질 수 있습니다. 즉, 현 음료를 옮겨야한다면 항상 다른 한 쪽으로만 옮길 수 있으며, 또 그 상자에 들어있는 음료도 다른 한 쪽으로만 옮길 수 있습니다. 이렇게 옮기는 일이 가능하려면 언제나 이동하는 방향의 다른쪽 끝이 비어있어야만 합니다.
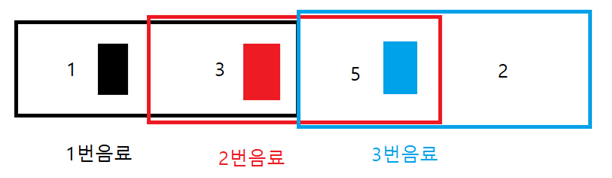
예시로 1번 음료가 {1, 3} 상자에 넣는 것이 가능하고, 2번 음료는 {3, 5}, 5번 음료는 {5, 2} 칸에 넣는 것이 가능할 때, 각 음료가 1번, 3번, 5번 상자에 들어가있을 때를 생각해봅시다. 이 때, 1번이나 3번 위치에 새로운 음료를 넣고 싶다면, 각 위치의 음료를 오른쪽으로 이동시켜 새롭게 2번 상자를 쓰는 것으로 새로운 상태를 만들어낼 수 있습니다.
위 그림과 같이 각 음료는 항상 두 개의 상자에만 넣을 수 있고, 한 상자에는 자기 자신이 들어가있기 때문에 다른 한 쪽으로 방향을 갖는 연결성이 생기는 것으로 볼 수 있습니다. 매 음료마다 하나의 방향만 갖기 때문에, 그 연결의 끝부분들은 언제나 비어있거나 차있는 두 경우 중 하나가 됩니다.
하지만 이 때, 연결되어있는 상자들 중, 두 개 이상 비어있는 경우는 절대 존재할 수 없습니다. 새로운 상자가 연결될 때에는 항상 새로운 상자는 최대 1개만 연결될 수 있지만, 이 연결을 위해서는 1개의 음료가 무조건 필요하게 됩니다. 즉, 상자의 수는 더 늘어날 수 없기 때문에, 어떤 연결된 상자들에는 최대 하나의 빈 상자만 존재할 수 있게 됩니다.
즉, 우리는 처음에 개별적으로 존재하는 상자들을 만든 다음, 1번부터 차례대로 음료들을 보면서 상자를 연결시키고, 항상 비어있는 상자의 정보만을 가지고 음료를 넣을 수 있는지 판단해주면 문제를 해결할 수 있습니다.
이를 위한 문제 해결 순서는 다음과 같습니다.
1) 현재 음료에 대해, 양쪽 상자가 모두 비어있다면 A 상자에 음료를 넣고, B상자가 비어있음을 표시한다. 그 후, A와 B상자를 연결한다. 2) A상자에만 음료가 들어있다면, B상자에 음료를 넣고 B상자와 A상자에 연결된 상자들을 연결한다. 이 때 A상자 연결의 끝이 비어있으면 비어있음을 표시한다. 3) B상자에만 음료가 들어있자면 2번과 비슷하게 A상자에 음료를 넣고 연결한다. 4) 만약 둘 다 비어있지않다면, 상자들 연결의 끝 위치를 사용하고 비어있는 상자가 없어졌음을 표시한다. 5) 4번에서 비어있는 상자가 없을 경우, 현 음료는 넣을 수 없다.
이 때, 연결관계를 표현하기 위한 좋은 자료구조로는 유니온 파인드(Union-find, Disjoint Set-Union) 자료구조가 있습니다. 이 때, 유니온-파인드의 맨 위에 존재하는 원소를 항상 비어있는 상자로 놓고, 만약 비어있지 않다면 비어있는 상자가 없음을 표시해줍니다. 이 자료구조를 이용해 상자들의 연결성을 쉽게 표현해줄 수 있어, $O(N^2)$에 문제를 해결해 줄 수 있습니다.
더 생각하면 이 때, 비어있는 상자를 알아내는 것 외의 연결관계는 의미가 없으므로, 경로 압축(추가로 랭크 압축)을 해주게 되면 시간복잡도가 크게 개선되어 평균적으로 $O(N)$에 가깝게 문제를 해결할 수 있습니다. 해당 내용은 위 유니온 파인드에 대한 링크에서 확인할 수 있습니다.
트럭 - ICPC Daejeon Nationalwide Internet Competition 2016 L번
관찰
우리는 언제나 최대 w대의 트럭이 올라갈 수 있는 다리에서 최대 하중 L을 넘지 않도록 트럭들을 순서대로 지나게 하여 n대의 모든 트럭이 다리를 건너가는 최소 시간을 구해야합니다.
가장 쉬운 방법으로는, 모든 시간을 직접 시뮬레이션하여 해결하는 방법이 있습니다. 다리의 위치를 1부터 w, 모든 트럭들을 w + 1 이후에 위치하게 놓은 다음, 가장 앞에 있는 트럭부터 1 단위 시간씩 시뮬레이션하는 것으로 문제를 해결할 수 있습니다.
이 때, 트럭이 놓이게 되는 경우는 5가지로 분류할 수 있습니다.
- 위치만 1 감소하는 경우
- 다리 앞에 있고, 위로 올라가서 다리에 가해지는 하중이 증가하는 경우
- 다리 앞에 있으나, 다리의 최대하중이 버티지 못해 올라가지 못하는 경우
- 다리를 지나가고 있는경우
- 다리를 모두 지나 다리에 가해지는 하중이 감소하는 경우
우리는 현재 다리에 가해지고 있는 하중 S를 고려하는 것으로, 항상 2번과 3번 상황인 다리 앞의 트럭이 올라갈 수 있는지 여부를 구해줄 수 있습니다. 또한 다리의 끝, 위치 1을 지나는 트럭을 통해 하중 S를 다시 구해줄 수 있고, 나머지 트럭이 다리에 올라올 수 있는지 여부를 구해줄 수 있습니다. 그리고 4번 경우인 다리를 지나가고 있는 트럭의 경우, 항상 앞으로만 이동하여 다리를 벗어나는 것이 중요하므로, 위의 모든 경우를 고려해줄 수 있습니다.
이 때에, 우리는 매 단위시간마다 모든 트럭들의 위치를 확인하고 하중을 관리해줘야 하므로, 최악에 $O(n * 최소시간)$의 시간이 필요하게 됩니다.
풀이
우리는 위 관찰 과정에서 굉장히 중요한 사실을 하나 알아낼 수 있습니다. 바로 4번 경우인 ‘트럭이 다리를 지나가고 있는 경우’ 입니다. 우리는 앞서 트럭이 다리를 건너가고 있다면, 항상 앞으로만 이동하여 최대한 빠르게 다리를 벗어나, 다리에 가해지는 하중을 감소시키는 것이 중요함을 알 수 있었습니다.
이것에서 중요한 정보을 알아낼 수 있을까요? 다리를 올라온 트럭은 항상 매 초마다 앞으로 이동할 수 있고, 이는 다리를 벗어날 때까지 계속 이어지기 때문에 매 초 1단위길이를 이동하게 됩니다. 다리의 길이는 총 w이므로, 우리는 다리를 t초에 올라온 트럭이 t+w초에 다리에서 내려간다는 사실을 알 수 있습니다.
즉, 우리는 트럭이 다리에 언제 올라가지는지만 알고있다면, 트럭이 언제 다리에서 내려오는지 알 수 있습니다. 이를 통해 모든 시간을 시뮬레이션하지 않고, 트럭들이 언제 다리에 오르고 내리는지 쉽게 알아낼 수 있을까요?
위 예시를 가지고 진행해보겠습니다.
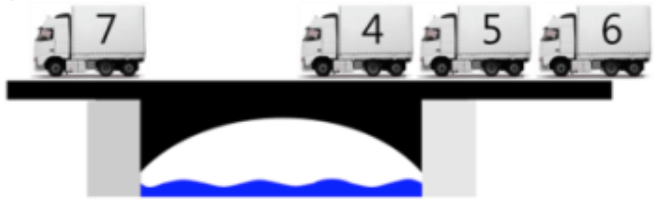
우리에겐 [7, 4, 5, 6] 4대의 트럭이 있고, 다리의 최대하중은 10, 길이는 2입니다.
현재 다리의 하중은 0이기 때문에, 첫 트럭 7은 시간 1에 바로 다리에 오를 수 있고, 앞선 관찰에 의해 1+2 = 3인 시간에 다리를 내려온다는 것을 알 수 있습니다.
첫 트럭이 다리에 오른 이후, 현재 다리의 하중은 7이기 때문에, 두 번째 트럭은 다리에 오를 수 없습니다. 이 때, 우리는 다리에 오른 트럭들이 어느정도 빠져나가는 시간 이후에만 두 번째 트럭을 다리에 올릴 수 있습니다. 다리 위에 가장 앞에 서있는 트럭은 7이기 때문에, 7이 빠져나간 때를 생각해보겠습니다.
7은 시간 3에 다리에서 내려오고, 그 때의 하중은 0이 됩니다. 이제 두 번째 트럭이 오를 수 있고, 다리에 트럭이 내려감과 올라감은 동시에 일어날 수 있으므로, 시간 3에 트럭 4가 다리에 올라 하중이 4가 되며, 시간 5에 내려오게 됩니다.
현재 하중은 4이므로, 트럭 5는 다리에 올라올 수 있고, 시간 4에 바로 올라올 수 있습니다. 하중은 9가 되며 현 트럭은 시간 6에 내려오게 됩니다.
현 하중은 9이므로, 트럭 6은 다리에 올라올 수 없습니다. 다리 위 가장 앞에 있는 4가 내려와도 하중은 5가되어 불가능하고, 트럭 5까지 내려와야 올라올 수 있게 됩니다. 그러므로 트럭 5가 내려오는 시간 6에 트럭 6은 올라오게 되며, 이 트럭은 시간 8에 내려옵니다.
이제 마지막 트럭까지 확인했으므로, 마지막 트럭이 내려오는 시간 8이 최소가 됩니다.
즉, 우리는 각 트럭이 다리에 올라가는 시간, 그리고 내려가는 시간을 알고 있는 상태에서, 모든 트럭들을 앞에서부터 뒤로 관리해줄 수 있는 자료구조만 있다면, 항상 트럭이 다리에 올라가야하는지, 내려와야하는지 2가지만 확인하는 것으로 문제를 해결할 수 있습니다.
항상 다리에 먼저 오른 트럭이 먼저 내려오기 때문에, 우리는 큐를 이용해서 위 트럭들을 관리해줄 수 있습니다.
모든 트럭들은 다리에 올라갈 때 한 번, 내려갈 때 한 번씩만 확인해주기 때문에, 우리는 $O(n)$의 시간복잡도에 문제를 해결할 수 있게 됩니다.
코드
방 청소
#include <bits/stdc++.h>
using namespace std;
int n, m;
int uftree[300010];
bool checkarr[300010];
void f_uftree_init(){ int i; for(i = 1; i <= n; i++) uftree[i] = i; }
int f_ances(int a){
if(a == uftree[a]) return a; return uftree[a] = f_ances(uftree[a]);
}
void f_solve(int a, int s){
if(!checkarr[a]){
checkarr[a] = 1; s = f_ances(s);
if(s != a) uftree[a] = s; printf("LADICA\n");
}else if(!checkarr[s]){
checkarr[s] = 1; a = f_ances(a);
if(a != s) uftree[s] = a; printf("LADICA\n");
}else if(checkarr[a] && !checkarr[f_ances(a)]){
a = f_ances(a); checkarr[a] = 1; s = f_ances(s);
if(!checkarr[s]) uftree[a] = s; printf("LADICA\n");
}else if(checkarr[s] && !checkarr[f_ances(s)]){
s = f_ances(s); checkarr[s] = 1; a = f_ances(a);
if(!checkarr[a]) uftree[s] = a; printf("LADICA\n");
}else printf("SMECE\n");
}
int main(){
int i, a, s;
scanf("%d %d", &m, &n);
f_uftree_init();
for(i = 0; i < m; i++){
scanf("%d %d", &a, &s);
f_solve(a, s);
}
return 0;
}
트럭
#include <bits/stdc++.h>
using namespace std;
int n, w, l;
int arr[1010], sarr[1010];
queue <int> q;
int main(){
int i, now = 0, cnt = 0;
scanf("%d %d %d", &n, &w, &l);
for(i = 0; i < n; i++) scanf("%d", &arr[i]);
i = 0;
while(1){
if(!q.empty() && i == sarr[q.front()]) now -= arr[q.front()], q.pop();
if(now + arr[cnt] <= l) sarr[cnt] = i + w, now += arr[cnt], q.push(cnt), cnt++;
if(cnt == n) break;
i++;
}
printf("%d", sarr[n - 1] + 1);
return 0;
}