Cryptanalytic Extraction of Neural Network Models

1. Introduction

이번 글에서는 암호학 분야에서 탑 티어 컨퍼런스 중 하나인 CRYPTO 2020에 통과된 Cryptanalytic Extraction of Neural Network Models 논문에 대해 알아보고자 합니다. 보통 암호학에서 인공지능을 활용할 때나 반대로 인공지능에서 암호학을 활용할 때에는 해당 기술을 마치 블랙박스와 같이 두고 결과를 가져다 쓰는 방식으로 진행되기 마련인데 이 논문에서는 그게 아니고 Neural Network Model의 Extraction을 하는 상황이 곧 암호학에서 아주 유명한 공격인 차분 공격을 하는 상황과 유사하다는 것을 이용해 Neural Network Model에 대한 Extraction을 기존의 방법들보다 더 효율적으로 진행하는 방법을 소개하고 있습니다.

암호학에서는 상당히 오래전부터 연구가 이루어졌던 차분 공격이 Neural Network Model의 Extraction에 어떻게 활용될 수 있는지, 구체적으로 어떠한 부분을 암호학으로부터 착안했고 방법은 어떠한지 등을 같이 알아보도록 하겠습니다.

2. Neural Network Models Extraction

기본적으로 Neural Network는 입력을 받아 여러 선형 연산과 비선형 연산을 거쳐 결과를 냅니다. 모델을 만들어낸 회사나 기관은 상당히 비싼 비용과 긴 시간을 들여 데이터를 수집하고 학습을 진행합니다. 그렇기 때문에 설령 해당 서비스를 공개해두고 다수의 사용자가 이를 이용해서 모델을 거친 후의 결과를 알 수 있게 할지언정 대부분의 경우 모델 자체를 공개하지는 않습니다. 반면 공격자의 입장에서는 모델에 자신이 만들어낸 입력을 넣었을 때 내부적으로 어떻게 동작하는지는 알 수 없고 결과만을 받아볼 수 있는 Black box 환경에서 모델을 추출하고 싶습니다. 이러한 상황은 마치 암호학에서 키를 모르는 공격자가 키를 복구하려는 공격과 유사하다고 생각할 수 있습니다. 즉 암호학에서 키를 모르는 공격자가 공격을 수행하는 것과 Neural Network Models Extraction을 하려는 공격자가 공격을 수행하는 것 모두 주어진 오라클에서 black-box로 공격을 수행한다는 점에 공통점이 있습니다.

또한 차분 공격에서 가장 핵심은 S-box와 같은 비선형연산에서 선형성을 찾는 것이라고 할 수 있는데, Neural Network 또한 선형 연산과 Activation function을 통해 발생하는 비선형연산이 결합된 형태이기 때문에 유사성이 있습니다.

즉 어떻게 보면 이 논문은 Neural Network의 동작을 오로지 선형 연산과 비선형 연산의 중첩 그 이상 그 이하도 아닌 것으로 고려합니다. Neural Network Model Extraction은 이전에도 관련 연구들이 존재하지만 이전의 결과와 비교했을 때 오로지 상황을 수학적인 함수의 중첩으로 생각해 암호학적 기법을 적용한 결과 대략 $2^{20}$배 더 정확한 값을 얻을 수 있었고 모델 추출을 위한 쿼리의 수 또한 1/100 정도로 크게 낮출 수 있었습니다.

3. Assumptions

정말로 임의의 모델에 대한 extraction이 가능하다고 하면 (내부적인 필터링이 없다고 할 때) 구글 어시스턴트, 애플 시리, 테슬라의 자율주행차 등의 모델을 전부 추출할 수 있음을 의미합니다. 하지만 아쉽게도 이 논문에서 소개하는 공격이 그 정도로 강력하지는 않고 여러 가정을 바탕에 두고 있습니다. 이 가정 중에서는 합리적인 가정도 있지만 강한 가정이라 다소 현실의 상황과는 맞지 않는 것도 있습니다. 가정들은 아래와 같습니다.

공격자는 Neural Network의 구조를 알고 있습니다(레이어가 몇 개인지, 각 레이어에 노드는 몇 개가 있는지 등).
임의의 입력을 넣을 수 있습니다.
출력 결과는 실수이고 계산된 값을 완벽하게 제공합니다. 예를 들어 개와 고양이를 분류하는 문제라고 할 때 단순히 개, 고양이로 결과를 주는 것이 아닌 0.2622351과 같은 정확한 값을 제공합니다.
연산은 64비트 부동소수점에서 진행됩니다.
Activation function은 ReLU입니다.

가정을 볼 때 2, 4번 가정은 그럭저럭 합리적이지만 1, 3, 5번 가정은 꽤 강한 가정이라는 생각이 듭니다. 특히 1, 3번의 제약조건으로 인해 아쉽지만 이 Extraction을 상용 모델에서 테스트해볼 수는 없습니다.

4. Differential Attack

암호학에서의 차분 공격에 대해 익숙하지 않다면 Introduction에 링크해둔 예전 포스팅을 참고하시는걸 추천드립니다.

암호학에서의 차분 공격이 $E(P), E(P \oplus \Delta)$ 사이의 관계식을 이용하는 것과 비슷하게, Neural network에서 선형 연산과 비선형 연산이 결합된 Neural network에서 입력에 약간의 차분을 더해 결과를 확인합니다. 구체적인 예시를 들어 설명해보겠습니다. 아래와 같은 모델을 생각해봅시다.

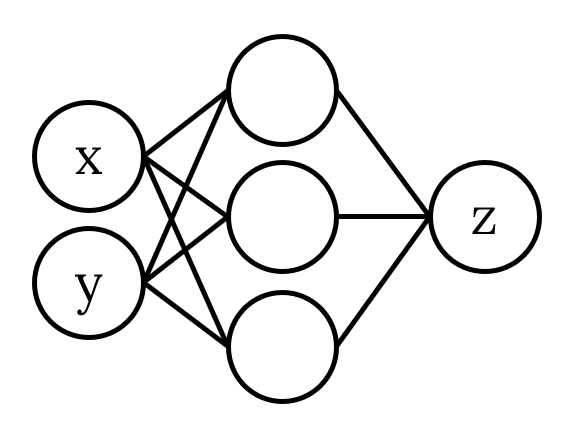
1-Deep Neural network이고 입력은 2차원, 출력은 1차원입니다. 위에서 서술한 가정과 같이 activation function은 ReLU라고 두겠습니다. ReLU의 특성상 입력이 0 부근만 아니면 입력에 대해 선형 값을 가집니다. 그렇기 때문에 x, y 값에 대한 z 값이 선형인 구간들을 나눠보면 아래의 그림과 같습니다.

중간에 있는 3개의 검정 선이 hidden layer의 각 노드에 대응됩니다. 같은 색으로 칠해진 영역들은 $x, y$에 대한 동일한 선형 식으로 나타내어지는 영역을 의미합니다.

실제 논문에서는 최적화를 위해 여러 가지 방법을 더 사용하지만 일단 기본적으로는 랜덤한 직선을 하나 정해 그 직선 위의 여러 점들에 대한 $z$ 값을 살펴봅니다. 이 때 이분탐색을 하며 선형성이 만족되지 않는 지점들을 찾으면 검정 선에 대한 정보를 얻어낼 수 있습니다. 이러한 지점을 critical point라고 부르고, critical point를 이용해 hidden layer를 하나씩 알아내면 전체 모델을 복구해낼 수 있습니다.

5. Implementation Details

아주 간단한 원리는 4. Differential Attack 에서 설명을 했지만 실제 공격을 수행할 때의 상황은 그렇게 간단하지 않고 여러 가지 고려해야 하는 점들이 많습니다. 실제 구현에서 고려해주어야 하는 요소들을 알아보겠습니다.

먼저 우리는 1-deep neural network를 아래와 같이 식으로 나타낼 수 있습니다. 식에서 $A^{(1)}, b^{(1)}$은 입력 layer에서 쓰이는 값이고 $A^{(2)}, b^{(2)}$는 첫 번째 hidden layer에서 쓰이는 값입니다.

\[f(x) = A^{(2)} \text{ReLU}(A^{(1)} x + b^{(1)} ) + b^{(2)}.\]

이 때 critical point가 발생했다는 의미는 적절한 입력 $x$ 근방에서 미세하게 값을 조정하면 어느 한 쪽은 뉴런이 활성화되고 반대쪽은 뉴런이 비활성화되게끔 만들 수 있다는 의미입니다. $f(x + \epsilon) - f(x)$와 $f(x) - f(x - \epsilon)$ 각각을 계산하면 $i$번째 뉴런에 대해 둘의 차가 $A^{(1)}_{j,i} \cdot A^{(2)}$가 됩니다. 이를 통해 각 뉴런에서의 파라미터를 복구한다고 할 때, 정확히는 원래 파라미터의 값을 얻는 대신 값에서 $\alpha$배가 곱해진 값을 얻게 됩니다. 뒷쪽에서 다른 파라미터에도 비슷하게 $\alpha’$배가 곱해지기 때문에 결국 상쇄가 되어서 이 스칼라 값이 곱해지는 것 자체는 결과에 영향을 주지 않습니다. 하지만 $\alpha$의 부호는 굉장히 중요합니다. Activation function이 ReLU이기 때문에 이 부호에 따라서 음수 범위가 비활성화 되는지 양수 범위가 비활성화 되는지 결정됩니다. 이 부호는 $f(x + \epsilon) - f(x)$와 $f(x) - f(x - \epsilon)$ 값을 가지고 부호를 양수 혹은 음수로 가정했을 때 모순이 생기는지 여부를 가지고 판단할 수 있습니다. 다만 이 때 부호를 결정하기 위해 필요한 쿼리의 수는 선형이지만 연산의 복잡도는 지수입니다.

또한 앞에서는 1-Deep Neural Network에 대한 공격을 설명했는데, layer가 1개보다 많은 $k$-Deep Neural Network에서는 상황이 조금 복잡해집니다. $k$-Deep Neural Network에서 첫 번째 layer를 분리해 $k-1$-Deep Neural Network으로 만들고 싶지만, 1-Deep Neural Network과는 다르게 찾아낸 critical point가 반드시 첫 번째 layer로 인해 발생한다는 보장을 할 수가 없습니다. 이를 해결하기 위해서 먼저 전체 뉴런의 수가 $N$개라고 할 때 총 $NlgN$개의 critical point를 구합니다. 그러면 각 뉴런에 대해 해당 뉴런과 관련이 있는 critical point가 적어도 2개는 있다고 생각할 수 있습니다. 동일한 뉴런으로부터 유도된 critical point라면 그 근방에서 두 값은 같은 선형 식을 가지게 됩니다. 그렇기 때문에 얻어낸 $NlgN$개의 critical point에 대해 둘씩 짝지어 그 근방의 값을 가지고 선형 식으로 나타낼 수 있는지 확인합니다.

글에서 언급한 것 이외에도 굉장히 다양한 구현 상의 디테일이나 이론적인 내용들이 있지만 생략하겠습니다.

5. Results

논문에서 소개된 공격에 대한 구현은 여기에서 확인할 수 있습니다.

이전의 논문들과 이 논문에서의 결과를 비교한 표는 아래와 같습니다.

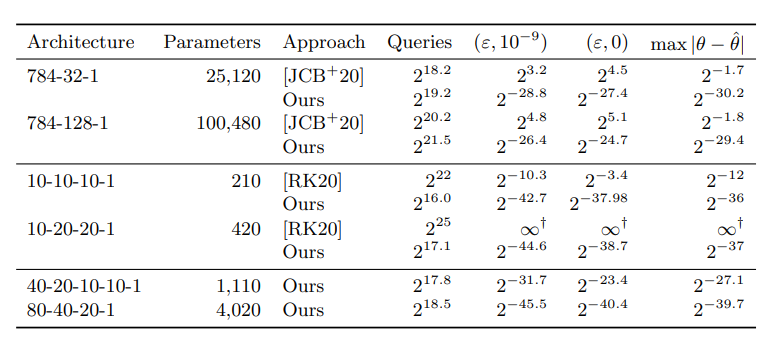
보면 쿼리의 수는 크게 차이가 나지 않는데 정확도는 아주 많은 개선이 있었음을 확인할 수 있습니다.

6. Conclusions

이 논문에서는 암호학에서 유명한 문제인 차분 공격의 원리를 가져와 Neural Network Models Extraction을 하는 방법에 대해 소개하고 있습니다. 예를 들어 MPC를 이용해 Neural Network를 사용자가 수행할 때 개인의 민감한 데이터가 회사에게 노출되지 않게 한다던가, 반대로 암호학에서 확률이 높은 차분 경로를 찾을 때 기계학습을 이용하다던가 하는 식으로 한쪽 연구의 결과를 가져와 유용하게 쓰는 경우는 쉽게 찾아볼 수 있지만 이 논문은 아예 근본적인 원리를 이용해서 크게 연관이 없어보이는 분야에서 효율을 높였다는 점이 흥미로웠습니다. 감히 제가 논문을 평가할 레벨은 아니지만 이 논문이 CRYPTO 2020에 통과된 이유도 비슷한 맥락이 아닐까 싶습니다.

또한 논문에서도 언급되어 있지만 차분 공격을 이용한 Extraction Attack은 이 논문에서 처음 제시된 방법이기에 발전 가능성이 많습니다. 차분 공격의 경우 High Order Differential Cryptanalysis, Impossible Differential Cryptanalysis, Truncated Differential Cryptanalysis 등의 여러 응용 방법이 있는 것 처럼 이 공격 또한 적절한 응용을 통해 계산 복잡도가 필요한 쿼리의 수를 감소시킬 수 있을 것으로 보입니다.