Improved Non-Interactive Zero Knowledge with Applications to Post-Quantum Signatures
1. Introduction
저번 글에서는 MPC를 이용한 Zero-Knowledge Proof에 대해 다루었습니다. 쉽게 요약을 해보자면 MPC-in-the-head를 이용해 증명자는 SHA256(x) = y를 만족하는 y를 알고 있다는 사실을 x를 공개하지 않고 검증자에게 납득시킬 수 있습니다. 더 나아가 원래의 증명은 검증자의 질의에 대해 증명자가 대답하는 방식으로 진행되나 Fiat-Shamir Transform을 사용하면 Non-Interactive로 증명을 만들 수 있습니다. 이렇게 Ishai et al.이 MPC-in-the-head를 제안한 후 Giacomelli et al.은 실제로 MPC를 수행하는 ZKBoo 프로토콜을 만들어냈습니다.
한편, Zero-Knowledge Proof로부터 전자서명을 만들 수 있습니다. 이건 사실 Non-Interactive Zero-Knowledge를 생각해보면 자명하게 이 Proof을 전자서명으로 활용할 수 있음을 짐작할 수 있습니다. NIZK로부터 만들어낸 전자서명은 타원 곡선에서의 이산 대수 문제, 정수에서의 이산 대수 문제, 정수에서의 소인수분해 문제 등을 기반 문제로 가지고 있는 기존의 전자서명들과 RSA와 다르게 오로지 해시의 충돌 저항성에만 의존한다는 장점이 있고, 무엇보다 Quantum Secure합니다. 그렇기 때문에 대표적으로 Picnic과 같은 양자 내성 암호 시스템에서 전자서명을 만드는 방법 중 하나로 사용되고 있습니다.
저희가 지금 지속적으로 다루고 있는건 MPC를 이용한 Non-Interactive ZK이지만, 사실 일반적으로는 SNARK라는 이름의 NIZK가 더 유명합니다. 또 이 SNARK로부터 파생된 STARK라는 NIZK도 있습니다. 이들을 모두 비교해보면 아래와 같습니다.
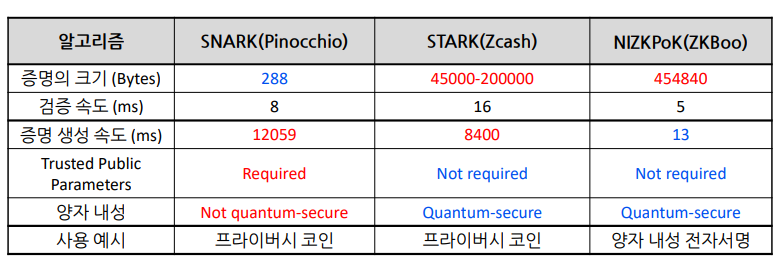
비교 표에서 볼 수 있듯 MPC를 이용한 NIZK는 증명의 크기가 굉장히 크지만 증명 생성 속도가 빠릅니다. SNARK는 프라이버시 코인에서 주로 쓰이는데, 비록 증명 생성 속도가 많이 느리지만 이 연산은 각 사용자가 알아서 하면 되므로 크게 중요하지 않고 증명의 크기가 압도적으로 작아 각 노드들이 공유해야 하는 데이터의 양이 적다는 이점이 크게 작용한 것으로 보입니다.
전자서명이 효율적인지를 확인할 수 있는 항목들로는 키의 길이, 서명의 길이, 서명의 생성 속도, 검증 속도 등이 있을 수 있습니다. NIZK를 이용한 전자서명은 비교적 최근에 제안된 구조이기 때문에 지속적으로 성능 면에서 발전이 이루어지고 있습니다.
이번 글에서 소개할 Improved Non-Interactive Zero Knowledge with Applications to Post-Quantum Signatures 논문에서는 MPC를 이용한 전자서명을 효율적으로 만들기 위한 새로운 NIZK 구조를 제안하고 있습니다. 이 논문은 크게
-
300-100,000개의 AND Gates를 가진 Circuit에서 다른 방법과 비교했을 때 가장 짧은 증명을 제공
-
기존 Picnic보다 3.2배 더 짧고 전자 서명 생성, 해시 기반 전자 서명(SPHINCS) 보다 짧음
-
파라미터 설정을 통해 서명의 크기와 연산량 사이의 trade-off 가능
-
효율적인 Ring/group 서명 방법 제시
이 4가지의 기여사항이 있습니다. 지금부터 구조를 같이 살펴보도록 하겠습니다.
2. ZKBoo
저번 글에서 ZKBoo까지 다루었다면 좋았겠지만 분량의 압박으로 인해 그러지 못했습니다. ZKBoo 구조도 재밌는게 많지만 글에서는 아주 간략하게만 다루도록 하겠습니다.
ZKBoo에서는 3명의 사용자가 MPC-in-the-head를 임의의 Circuit $C$에 대해 수행할 수 있게 하는 Circuit decomposition을 제안했습니다.
Circuit decomposition이라 함은 곧 Circuit $C$와 입력 $x$를 3개로 나누어야 하고, 이 때 사용자의 관점 2개를 검증자에게 제공해도 검증자는 $x$에 대한 아무런 정보를 얻지 못한다는 Zero-knowledge 성질이 만족되어야 합니다.
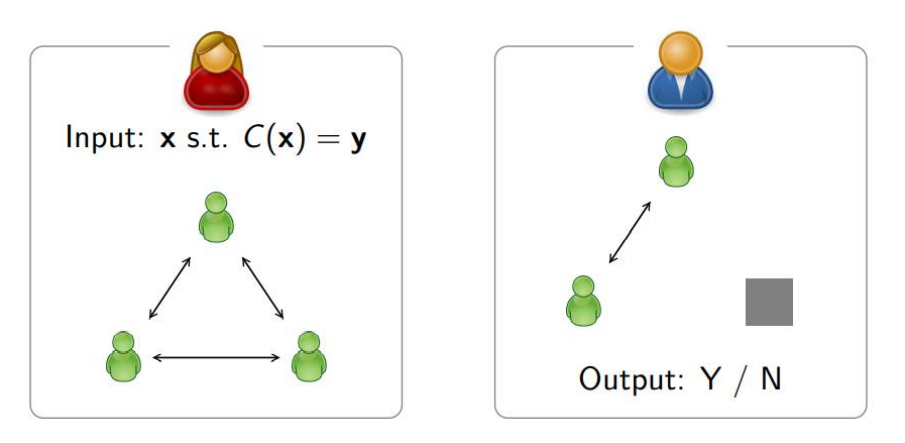
이 Circuit decomposition을 어떻게 해야하는가는 나름의 자세한 설명이 필요하지만 생략하고 간략한 그림만 보여드리겠습니다.
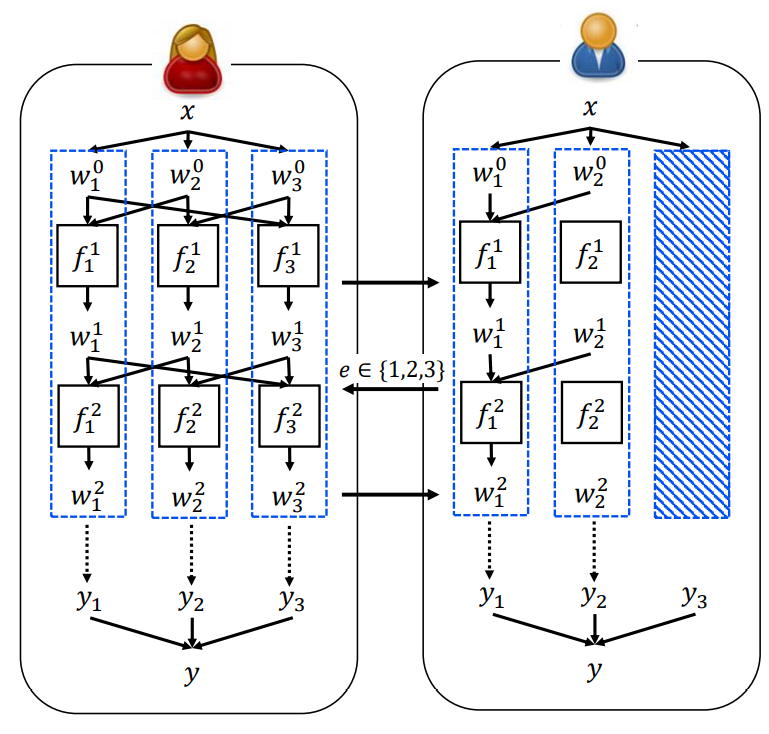
왼쪽의 빨간색 사람이 증명자, 파란색 사람이 검증자입니다. 증명자는 $x$를 3개로 나눠 각각 계산을 수행하고 이들을 commit합니다. 검증자는 3개 중에서 자신이 원하는 2개의 관점을 확인합니다. 검증자는 이 결과로부터 MPC 결과가 올바른지 확인합니다.
예를 들어 증명자가 SHA256(x) = y인 x를 알고 있다라고 주장했을 경우, 검증자는 자신이 확인한 관점 2개로부터 $x$를 알아낼 수는 없지만 결과가 $y$가 나왔다는 사실로부터 증명자가 $x$를 알고 있다고 인정할 수 있습니다.
그런데 만약 악의적인 증명자가 검증자를 속이려고 한다면 어떨까요? 즉, 증명자는 SHA256(x) = y인 x를 모르지만 검증자에게 자신이 이를 알고있는척 하려고 합니다.
만약 그렇다면 적어도 어느 한 관점은 잘못된 계산을 포함할 수 밖에 없고, 검증자는 $1/3$의 확률로 이를 알아차릴 수 있습니다. 악의적인 증명자가 검증자를 속이는데 성공할 확률(Soundness error)은 $2/3$이고, $2^{-80}$의 Soundness error를 달성하기 위해서는 137번의 반복이 필요합니다.
3. 핵심 아이디어
ZKBoo를 보고 이 논문에서 제시하는 핵심 아이디어는 Soundness error를 낮춰서 반복을 줄이자는 아이디어입니다. 반복이 많으면 많을수록 검증 시간, 서명 크기, 생성 시간 등에 전부 영향을 주니 상당히 합리적인 생각입니다.
구체적으로 $n$명이 참여하는 MPC-in-the-head에서 검증자가 $n-1$개의 관점을 확인한다면 soundness error는 최대 $2/n$입니다. $n$명중에서 $A$, $B$가 주고받은 관점에서 문제가 있다고 할 때, 검증자가 $A$ 혹은 $B$ 둘 중 한명을 빼놓는다면 soundness error가 발생하기 때문입니다. ZKBoo에서는 $n = 3$이었기 때문에 soundness error가 $2/3$이었습니다.
soundness error가 작다는 것은 곧 반복을 줄일 수 있다는 의미이기 때문에 $n$이 커지면 커질수록 soundness error가 낮아집니다.
그러나 ZKBoo 구조에서 단순히 $n$을 늘리는 것이 능사는 아닌 것이, ZKBoo의 Circuit decomposition을 $n$명에 대해 진행한 후 $n-1$개의 관점을 검증자에게 준다면 검증자는 $\binom{n-1}{2}$개의 쌍에 대해 모순이 없는지(=consistency)를 확인해야 해서 검증 시간이 상당히 오래 걸리게 됩니다.
이 문제를 타개하기 위해 논문에서는 Preprocessing phase를 도입해 $n$의 제곱에 비례하는 연산 대신 $n$에 비례한 연산이 필요하도록 하고 여러 optimization을 통해 증명의 크기가 $n$과 독립적인 효율적인 영지식 증명을 개발했습니다.
4. NIZK 과정
NIZK 과정에서 n-out-of-n secret sharing이라는 용어가 나와서 이를 먼저 보겠습니다.
비트 $b \in {0,1}$을 n-out-of-n secret sharing한다는 의미는 $b$의 부분 정보를 $n$명이 나눠가지고, $n$명이 모두 모이기 전까지는 $b$를 알아낼 수 없게 한다는 의미입니다.
n-out-of-n secret sharing을 하는 방법은 굉장히 간단합니다. $x_1, x_2, \dots , x_{n-1}$ 값을 랜덤으로 정하고 $x_n = b \oplus x_1 \oplus x_2 \oplus \dots , x_{n-1}$로 두면 $x_{1…n}$은 $b$에 대한 n-out-of-n secret sharing이 됩니다.
이 논문에서 제안된 NIZK는 주어진 circuit에서 각 wire에 모두 값을 마스킹하고 마스킹한 값을 n-out-of-n secret sharing해서 검증자가 $n-1$개의 관점을 보더라도 출력 비트에 대한 정보를 얻지 못하게 하는 방법을 사용합니다.
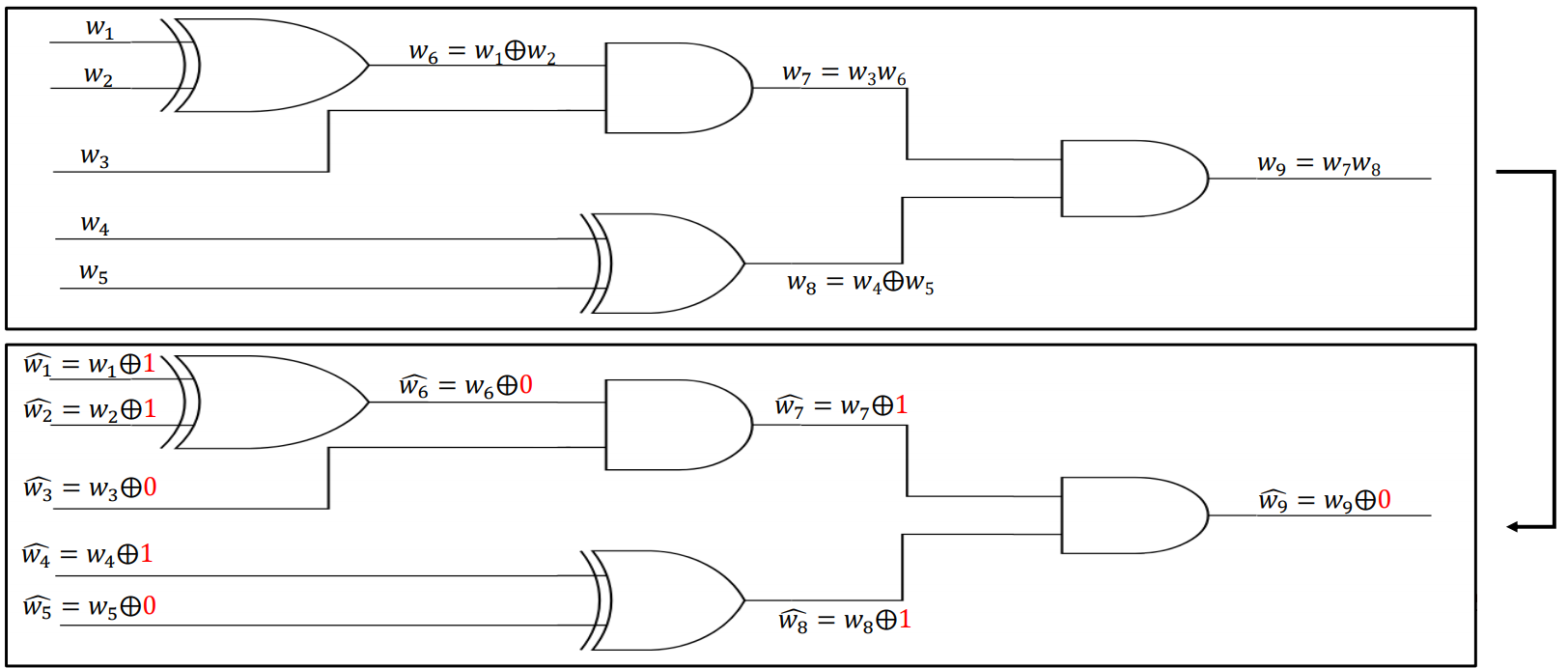
위의 그림을 참고해서 설명을 하겠습니다. 증명자가 SHA256(x) = y인 $x$를 알고 있다는 것을 증명하고 싶다고 할 때, SHA256을 나타낸 회로에서 x를 곧이곧대로 입력에 넣은 결과를 검증자에게 알려줄 수는 없습니다. 대신 2번째 그림의 Input wire($\hat{w_1}, \hat{w_2}, \hat{w_3}, \hat{w_4}, \hat{w_5}$)처럼 0 혹은 1을 XOR해서(=마스킹을 해서) 연산을 수행합니다.
검증자는 $n-1$개의 관점만을 얻으므로 이 관점들로부터 입력 $x$, 즉 $w_1, w_2, w_3, w_4, w_5$가 무엇인지 알 방법이 없습니다.
각 wire에 마스킹이 되는 값은 논문에서 $\lambda$로 표기하고 있습니다. Input wire와 AND 게이트의 output wire에 대해서는 미리 preprocessing 단계에서 마스킹 값을 정해야 하고 XOR 게이트의 output wire에서는 input wire에서의 마스킹 값의 XOR로 결정됩니다. 그 이유는 아래의 그림과 같습니다.
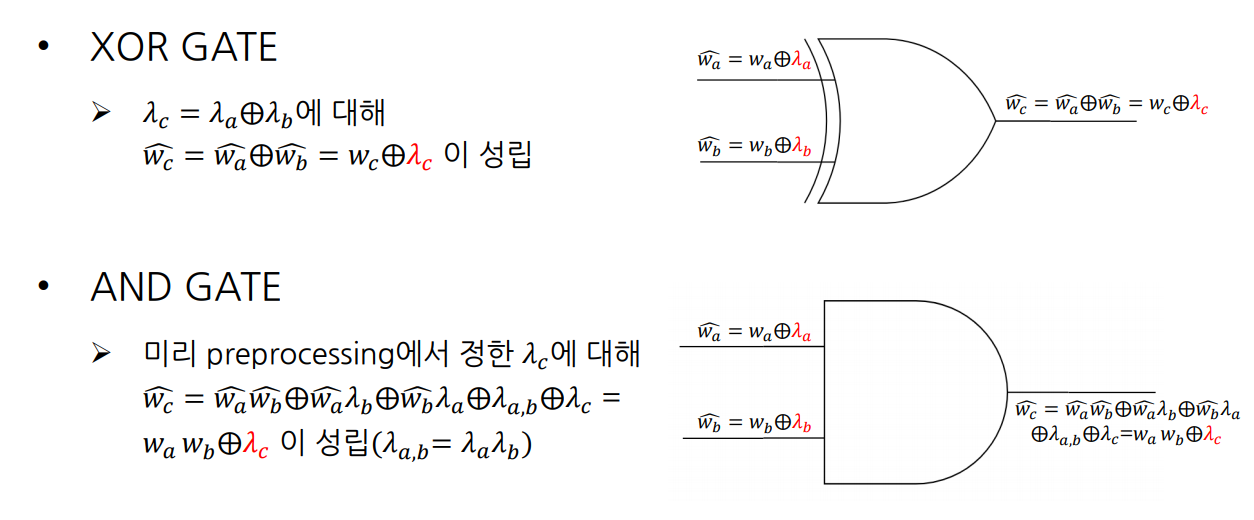
이렇게 마스킹 값을 정한 다음에 $n$명이 각자 자신의 연산에서 사용하는 마스킹 값 $\lambda^{1…n}_c$는 $\lambda^1_c \oplus \lambda^2_c \oplus \dots \oplus \lambda^n_c = \lambda_c$를 만족합니다. 결정된 마스킹 값에 따라 각 사용자는 MPC를 진행합니다.
5 Round Zero-Knowledge Proof
과정에서 볼 수 있듯 이전과 다르게 Preprocessing 단계가 추가되었습니다. 그런데 만약 증명자가 올바르지 않은 마스킹 값을 선정하더라도(예를 들어 $\lambda^1_c \oplus \lambda^2_c \oplus \dots \oplus \lambda^n_c = \lambda_c$를 만족하지 않는 $\lambda^{1…n}_c$를 선정) 검증자는 이는 알아차릴 방법이 없습니다.
이 문제를 해결하기 위해 MPC 이전에 Preprocessing을 위한 2 Round의 interaction이 추가됩니다.
해결방법은 어떻게 보면 굉장히 직관적이고 어떻게 보면 굉장히 단순무식(?)한 방법을 사용하는데, 마스킹 값의 집합을 $m$개 만들어둔 후 검증자가 택한 $m-1$개의 집합을 공개합니다.
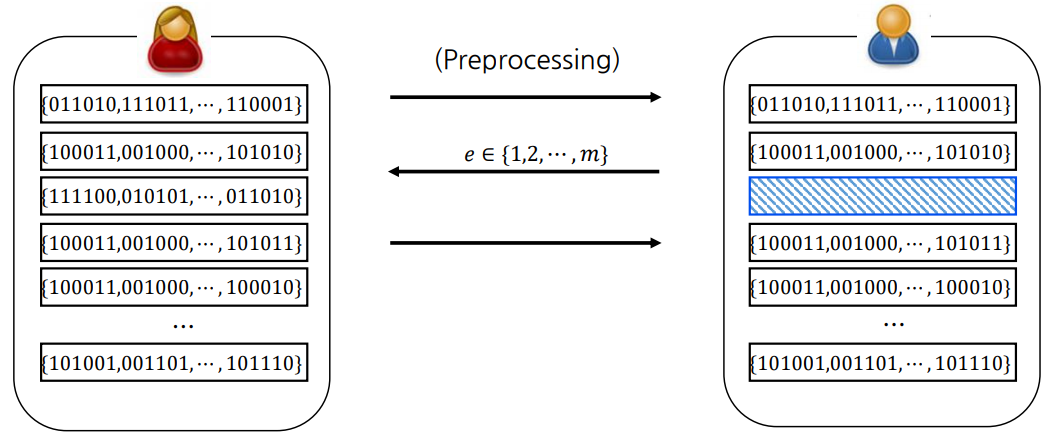
이후 공개하지 않은 마스킹 값의 집합을 이용해 MPC-in-the-head 절차를 진행합니다.
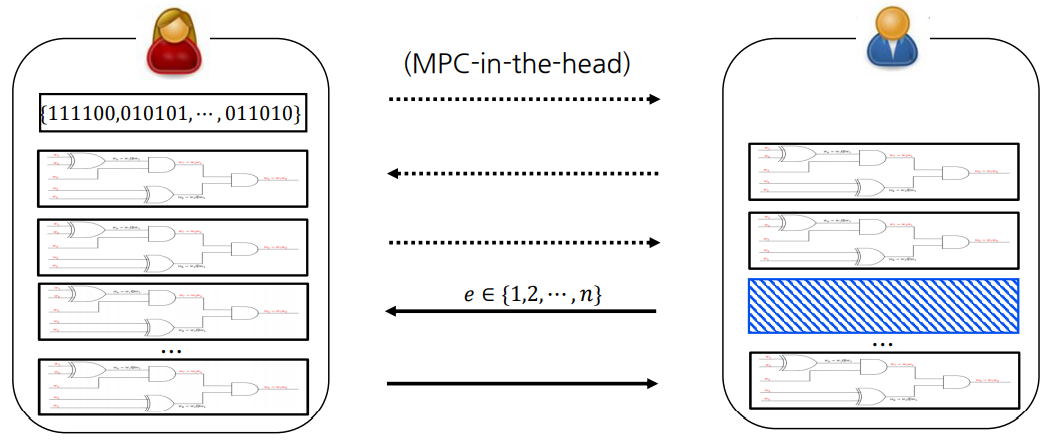
3 Round Zero-Knowledge Proof
이 5 Round Zero-Knowledge Proof를 3 Round Zero-Knowledge Proof으로 줄일 수 있습니다. 증명자가 Preprocessing 단계에서 미리 MPC-in=the-head를 전부 진행해두고 검증자는 선택할 마스킹 값의 집합과 MPC-in=the-head에서 확인할 연산 결과의 인덱스를 한 번에 전송하면 됩니다.
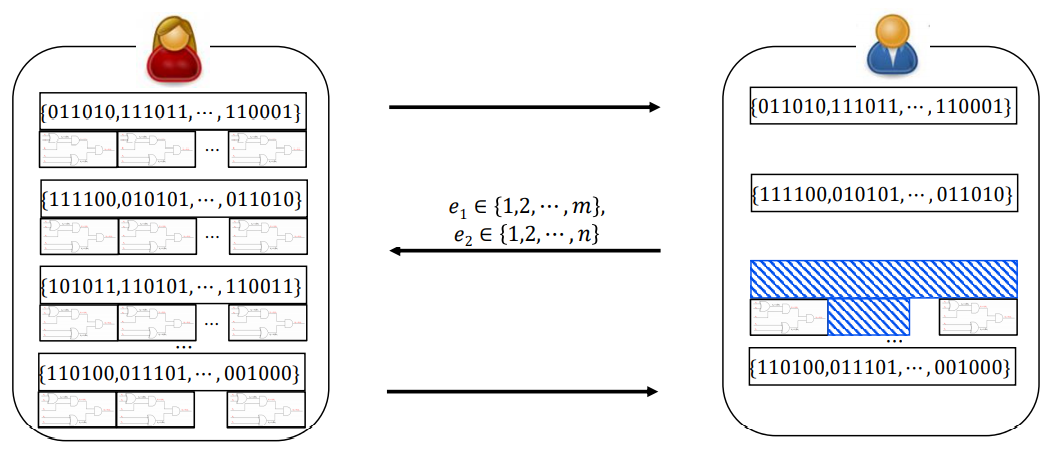
5. Optimizations
위에서 설명한 방법을 곧이곧대로 구현하면 ZK를 잘 수행할 수 있지만 한편으로 성능이 좋지 않습니다. 그렇기 때문에 다양한 Optimization을 통해 성능을 개선해야 합니다. 그 기법들을 알아보겠습니다.
A. 시드를 이용한 마스킹 값 생성
Preprocessing 단계에서 증명자는 마스킹 값을 랜덤하게 만들어내야 합니다. 이 때 마스킹 값 전체를 랜덤하게 만든 후 검증자에게 넘겨주는 대신 seed만을 넘겨주고 Pseudo Random Function을 통해 동일한 마스킹 값을 증명자와 검증자가 공유하도록 프로토콜을 만들면 오가는 데이터의 양을 줄일 수 있습니다.
B. 이진 트리 기법
$m$개의 시드를 전부 검증자에게 제공하는 대신 $m$개의 시드를 트리의 리프로 관리하고, 각 트리의 노드는 부모로부터 계산 가능하도록 구조를 만들면 $m-1$개의 시드를 검증자에게 주기 위해서 $\text{log} m$개 만큼의 정보만 제공하면 됩니다. 이 기법은 Merkle Hash Tree 등에서 자주 보이는 기법입니다.
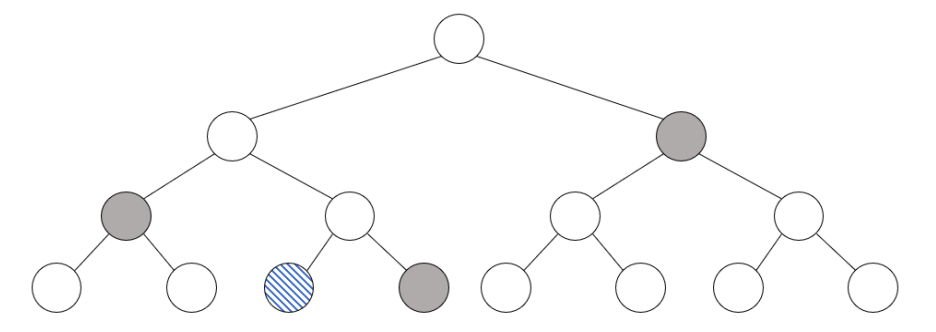
C. Preprocessing 단계에서의 시드 공개 개수
기존 프로토콜에서는 검증자가 $m-1$개의 마스킹 값을 확인합니다. 대신 $m - \tau$개를 공개하고 공개하지 않은 $\tau$개를 MPC-in-the-head에서 사용하면 한 번의 Preprocessing으로 $\tau$번 MPC-in-the-head를 진행할 수 있습니다.
그러나 이 경우 preprocessing에서의 soundness error가 $1/m$보다 증가하기 때문에 이를 고려한 최적의 $\tau$ 값은 아래의 표와 같습니다.
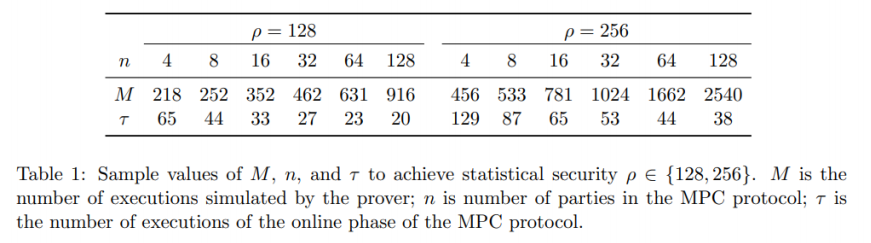
6. Results & Conclusions
최종적으로 Circuit에서의 AND Gates 개수에 따른 Performance를 그래프로 나타내면 아래와 같습니다.
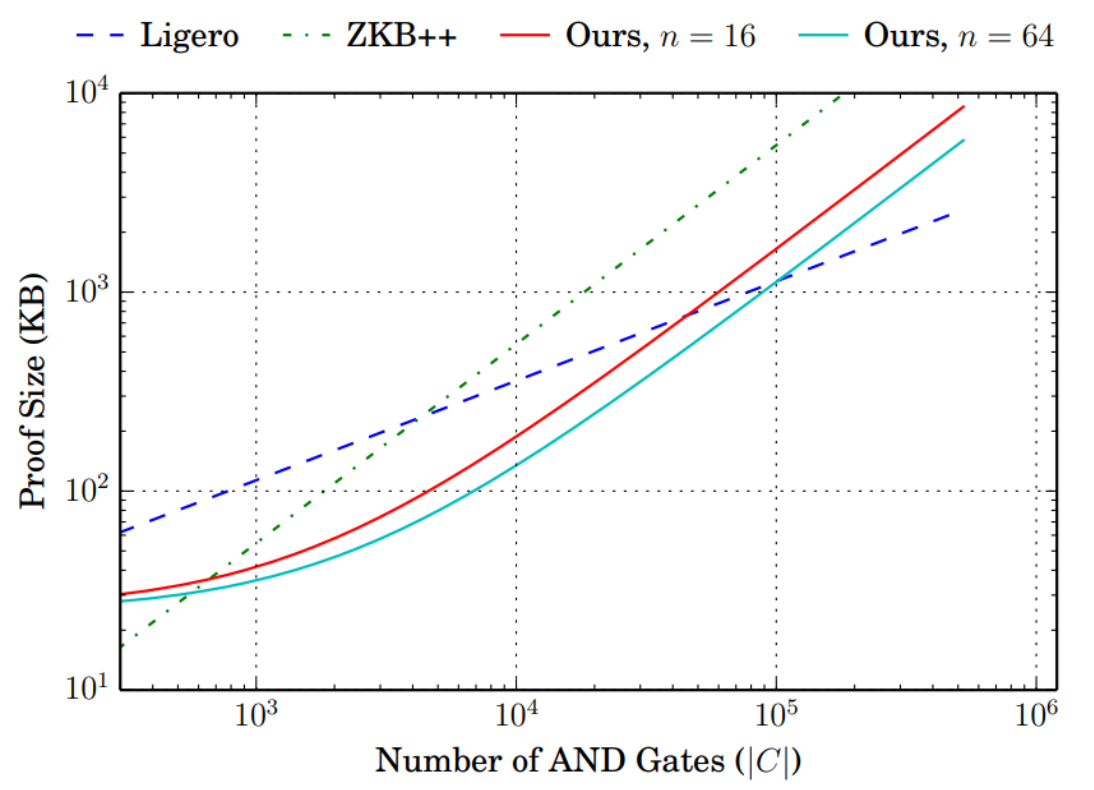
그래프에서 빨간색/초록색으로 표시된 것이 이 논문의 방법으로 구현한 전자서명입니다. 기존의 방법과 비교할 때 AND 게이트가 300에서 100,000개 정도일 때 효율적임을 알 수 있습니다.
해시함수, 암호화 알고리즘 등 우리가 “암호학적으로” 의미를 가지는 대부분의 알고리즘은 저 범위 안에 들어가기 때문에 이 방법이 기존의 방법보다 효율적임을 알 수 있습니다.
이번 글을 통해 개선된 NIZK와 전자서명을 소개했습니다. NIZK를 이해하는데 이 포스팅이 도움이 되기를 바라며 글을 마치도록 하겠습다다.