cheetose's profile image

cheetose

May 19, 2021 00:00

Wireless Digital Communication 1

communication

서론

무선 통신 시스템은 현대 사회에서 없어서는 안될 시스템입니다. 음성 통신을 위한 휴대전화부터 인터넷을 사용하는 것까지 저희가 실생활에서 겪는 수많은 일에 무선 통신이 반드시 필요합니다. 그렇다면 어떻게 A라는 사람이 전송한 데이터가 수백 km 떨어져있는 B라는 사람에게 정확하게 도착할 수 있을까요? 앞으로 오랜 시간에 걸쳐서 이 질문에 대한 대답을 해보려고 합니다.

이 시리즈가 총 몇 개의 글로 이루어질지는 정확히 예측이 안되지만, 최종적으로는 현재 LTE, 5G 시스템에서 사용되는 OFDM 방식을 설명하는 것을 목표로 하고자합니다. 우선 첫 글에서는 가장 기본적인 시스템인 Binary modulation에 대해서 간단하게 설명하고 넘어가겠습니다.

본론에 들어가기에 앞서 앞으로 나올 용어들에 대한 설명을 하겠습니다.

  • $s_m(t)$ : 송신 메시지를 의미합니다.
  • $r(t)$ : 수신 메시지를 의미합니다.
  • $\psi(t)$ : basis function을 의미합니다. 이것을 통해 $s_m(t)$를 표현할 때 $\sum_{i=1}^{N}s_{mi} \psi_i(t)$으로 나타낼 수 있습니다.
  • $\varepsilon_m$ : 메시지의 에너지를 의미합니다.
  • $\varepsilon_b$ : 메시지의 비트당 에너지를 의미합니다. 한 번에 전송하는 비트가 $N$개 일 때 $\varepsilon_b = \frac{\varepsilon_m}{N}$의 관계입니다.
  • $R_b$ : bit rate. 1초에 전송하는 비트 개수를 의미합니다.
  • $T_b$ : bit interval. 1bit를 전송하는데 걸리는 시간을 의미합니다. $R_b = \frac{1}{T_b}$의 관계입니다.
  • constellation : 전송하고자 하는 데이터의 종류가 여러 개일 때, 그것들을 모아놓은 다차원 벡터의 집합을 의미합니다.

본론

기본적인 무선 통신 시스템의 송신단의 구조는 아래의 그림과 같습니다.

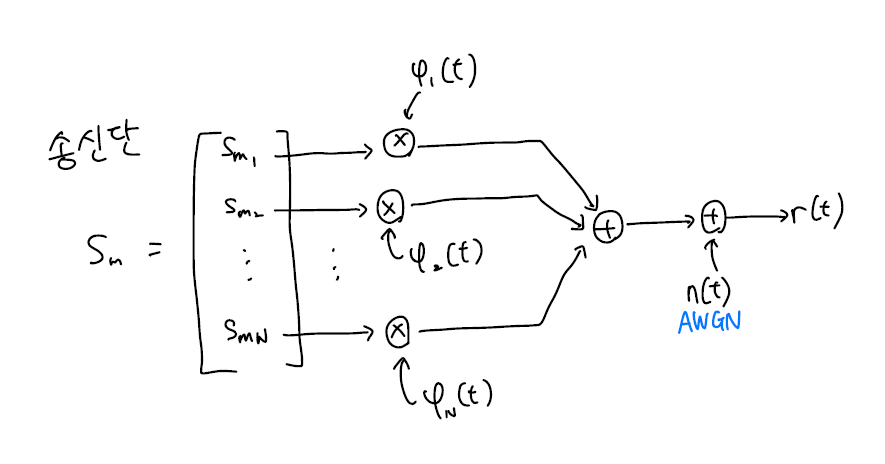
modulation

$N$은 signal vector의 dimension 이고 ${\psi_i}$는 orthonormal set입니다. ${\psi_i}$가 orthonormal 해야하는 이유는 추후에 서술하겠지만 demodulation을 쉽게 하기 위함입니다.

우선은 noise가 없고, 송수신단에서 1개의 bit만 주고 받는 시스템에서의 modulation에 대해서 알아보겠습니다.

Binary Modulation

Binary modulation은 0을 보낼 때는 $s_1(t)$라는 신호를, 1을 보낼 때는 $s_2(t)$라는 신호를 만들어 전송하는 것을 의미합니다. 이 때 신호의 종류가 2개이기 때문에 basis function의 개수도 1개 또는 2개입니다.

$s_m(t)$를 어떻게 정의하는가에 따라서 다양한 modulation 방식이 존재합니다. 지금부터 다양한 Binary modulation의 종류와 각 modulation방식의 특징을 알아보겠습니다.

우선 basis function이 1개인 Binary Antipodal Signal에 대해서 알아보겠습니다. 이름에서 알 수 있듯이 signal의 부호를 통해 메시지를 구분하는 방식입니다.

Binary Pulse Amplitude Modulation(PAM)

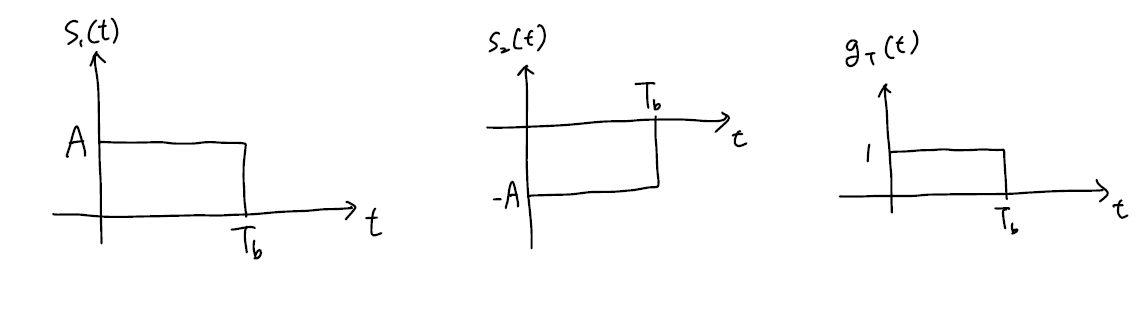
PAM signal

PAM 방식은 각 신호가 위의 그림과 같은 방식을 말합니다. $g_T(t)$를 오른쪽 그림처럼 Amplitude가 1인 rectangular function으로 정의하면 $s_m(t) = \pm A g_T(t)$라 할 수 있습니다. 각 메시지의 에너지는 $\varepsilon_m = \int_{-\infty}^{\infty}{s_m^{2}(t)dt} = A^{2}T_{b}$ 입니다. 또한 basis funtion의 dimension이 1이기 때문에 $\varepsilon_b = \varepsilon_m$을 만족합니다. 이 관계는 모든 Binary modulation 방식에서 똑같이 적용됩니다.

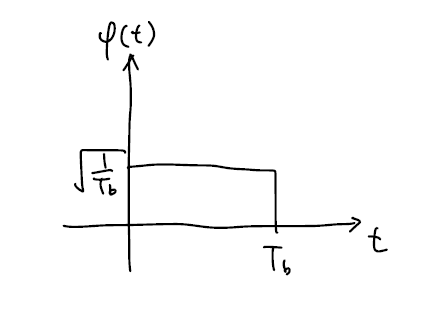
PAM basis function

basis function을 위 그림과 같이 $\psi(t) = \sqrt{\frac{1}{T_b}}, (0 \leq t \leq T_b)$로 잡게 된다면 $s_1(t)=s_{m1}\psi(t)$, $s_2(t)=s_{m2}\psi(t)$라 할 때, $s_m = \pm A \sqrt{T_{b}} = \pm \sqrt{\varepsilon_{b}}$이 되므로 constellation을 그려보면 아래와 같이 됩니다.

PAM constellation

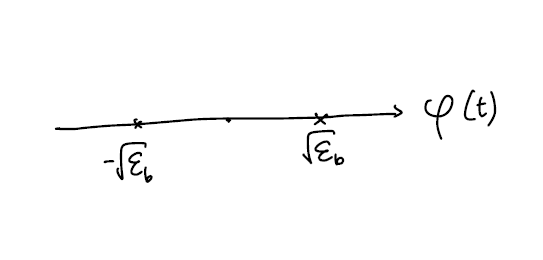
Binary Amplitude Shift Keying (ASK)

ASK 방식은 $s_1(t) = \sqrt{\frac{2\varepsilon_b}{T_b}}cos(2\pi f_{c}t)$, $s_2(t) = -\sqrt{\frac{2\varepsilon_b}{T_b}}cos(2\pi f_{c}t)$인 방식을 말합니다. basis function을 $\psi(t) = \sqrt{\frac{2}{T_b}}cos(2\pi f_{c}t)$로 잡는다면 constellation은 아래 그림과 같아질 것입니다.

ASK constellation

ASK의 constellation과 PAM의 constellation이 같은 것을 확인할 수 있습니다. 실제로 같은 그림을 재활용 했습니다. 이는 PAM 기법과 ASK 기법의 성능 차이는 없고 demodulation 결과가 basis function에 무관하다는 것을 의미합니다.

demodulation

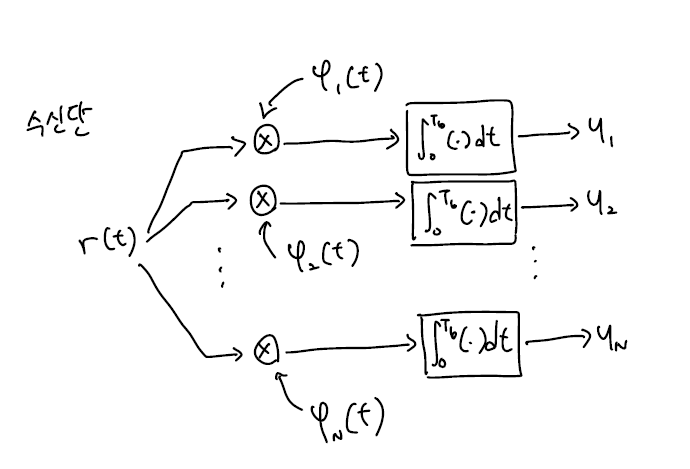
demodulation

무선 통신 시스템의 수신단의 구조는 위 그림과 같습니다.

basis function이 1개 있을 때 demodulation은 다음과 같은 과정을 거쳐 진행됩니다. 여기서 $r(t)$는 수신된 신호를 의미합니다.

$r(t) = s_m \psi(t)$일 때,

$\int_{0}^{T_b}{r(t)\psi(t)dt}$ $= \int_{0}^{T_b}{s_m\psi^{2}(t)dt}$ $= s_m\int_{0}^{T_b}{\psi^{2}(t)dt}$ $= s_m$

위 식에서 $\psi(t)$가 normalized 되었으므로 $\int_{0}^{T_b}{\psi^{2}(t)dt} = 1$이라는 사실을 이용했습니다. 즉, 수신된 신호에 basis function을 곱하여 신호 구간에 대해 적분하면 송신단에서 전송한 신호가 무엇인지 알 수 있습니다.

Binary orthogonal signal

위의 두 방식은 $s_m(t)$의 부호만 달라 signal set의 dimension이 1이었습니다. 다음으로 설명할 방식들은 2개의 signal이 서로 orthogonal한 방식으로 dimension이 2가 됩니다. 따라서 basis function의 개수도 2개가 되고, constellation 역시 2차원으로 표현됩니다.

Binary Pulse Position Modulation (PPM)

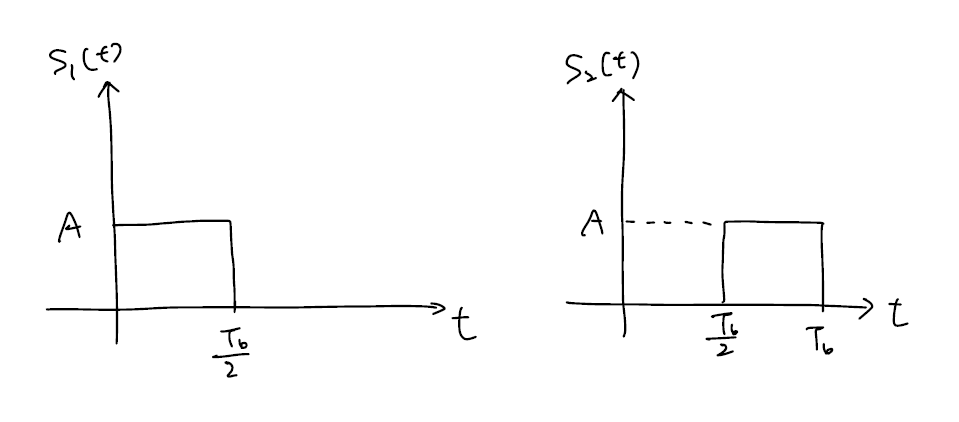
PPM signal

PPM 방식은 이름과 위 그림에서 알 수 있듯이 pulse의 위치로 메시지를 구분하는 방법입니다. $\int_{0}^{T_b}{s_{1}(t)s_{2}(t)dt} = 0$ 이므로 두 신호가 orthogonal 함을 알 수 있습니다. 이 신호의 에너지를 구해보면 $\varepsilon_m = \int_{0}^{T_b}{s_m^{2}(t)dt} = A^{2}\frac{T_b}{2}$ 입니다.

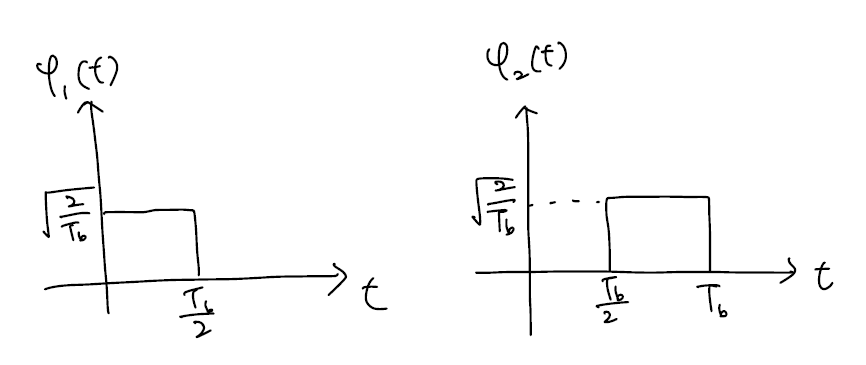
PPM basis function

basis function을 위 그림처럼 잡아보겠습니다. 그렇다면 아래의 식과 같은 관계가 성립합니다.

  • $s_1(t) = s_{11}\psi_1(t) + s_{12}\psi_2(t) \rightarrow s_1 = [s_{11}\quad s_{12}] = [\sqrt{\varepsilon_b}\quad 0]$
  • $s_2(t) = s_{21}\psi_1(t) + s_{22}\psi_2(t) \rightarrow s_1 = [s_{11}\quad s_{12}] = [0\quad \sqrt{\varepsilon_b}]$

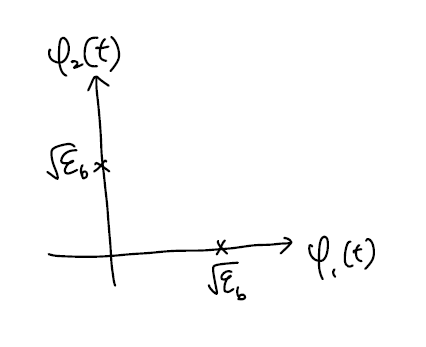
PPM constellation

이를 이용하여 constellation을 그려보면 위 그림과 같이 나오게됩니다.

Binary Frequency Shift Keying (FSK)

BFSK는 두 신호가 아래와 같은 modulation 방식입니다.

  • $s_1(t) = \sqrt{\frac{2\varepsilon_b}{T_b}}cos(2\pi f_1t)$, for $0 \leq t \leq T_b$
  • $s_2(t) = \sqrt{\frac{2\varepsilon_b}{T_b}}cos(2\pi f_2t)$, for $0 \leq t \leq T_b$

여기서 $f_1 = \frac{k_1}{2T_b}$, $f_2 = \frac{k_2}{2T_b}$($k_1$과 $k_2$는 서로 다른 정수)꼴이어야 두 신호가 orthogonal이 됩니다. 증명은 아래와 같습니다.

$\int_{0}^{T_b}{s_1(t)s_2(t)dt}$ $= \frac{2\varepsilon_b}{T_b}\int_{0}^{T_b}{cos(2\pi f_1t)cos(2\pi f_2t)dt}$ $= \frac{\varepsilon_b}{T_b}\int_{0}^{T_b}{cos(2\pi (f_1+f_2)t) + cos(2\pi (f_1-f_2)t)dt}$

보통 통신에서 사용하는 주파수 대역이 GHz단위이기 때문에 $\int_{0}^{T_b}{cos(2\pi (f_1+f_2)t)dt}$는 0이라고 가정할 수 있습니다. 계속 이어서 쓰면

$= \frac{\varepsilon_b}{T_b}\int_{0}^{T_b}{cos(2\pi (f_1-f_2)t)dt}$ $= \frac{\varepsilon_b}{T_b}\frac{1}{2\pi(f_1-f_2)}[sin(2\pi(f_1-f_2)t)]_{t=0}^{T_b}$ $= \frac{\varepsilon_b}{T_b}\frac{1}{2\pi(f_1-f_2)}sin(2\pi(f_1-f_2)T_b)$ $= \frac{\varepsilon_b}{T_b}\frac{1}{2\pi\Delta f}sin(2\pi\Delta f T_b), \Delta f = f_1-f_2$ $\therefore$ $\Delta f = \frac{k}{2T_b}, (k$는 0이 아닌 정수$)$ 꼴이면 위의 식이 0이 되므로 orthogonal하다는 사실을 확인할 수 있습니다. 참고로 $k=0$이면 둘은 완전히 동일한 신호가 되므로 그런 일은 없도록 해야합니다.

이것도 PPM과 마찬가지로

  • $s_1(t) = s_{11}\psi_1(t) + s_{12}\psi_2(t) \rightarrow s_1 = [s_{11}\quad s_{12}] = [\sqrt{\varepsilon_b}\quad 0]$
  • $s_2(t) = s_{21}\psi_1(t) + s_{22}\psi_2(t) \rightarrow s_1 = [s_{11}\quad s_{12}] = [0\quad \sqrt{\varepsilon_b}]$

의 형태로 표현할 수 있고, 따라서 constellation 역시 같은 결과를 나타냅니다. 즉, PPM과 FSK역시 demodulation의 성능이 동일하다는 것을 알 수 있습니다.

demodulation

binary orthogonal에서는 수신된 메시지가 $r(t) = s_{m1} \psi_1(t) + s_{m2} \psi_2(t)$입니다. 우리의 목적은 $s_{m1}$과 $s_{m2}$가 무엇인지 알아내는 것입니다. 이 과정은 binary antipodal 시스템에서와 매우 유사합니다. 우선 $s_{m1}$을 구하려면 다음과 같이 처리하면 됩니다.

$\int_{0}^{T_b}{r(t)\psi_1(t)dt}$ $= \int_{0}^{T_b}{s_{m1}\psi_1^{2}(t)+s_{m2}\psi_1(t)\psi_2(t)dt}$ $= s_{m1}$

여기서 $\psi_1(t)$와 $\psi_2(t)$가 orthonormal하기 때문에 $\int_{0}^{T_b}{\psi_1^2(t)dt}=1$, $\int_{0}^{T_b}{\psi_1(t)\psi_2(t)dt}=0$이므로 위의 식이 성립합니다. 정리하자면 $s_{m1}$을 구하기 위해서는 수신 신호에 $\psi_1(t)$를 곱하고 신호 구간에 대해 적분을 해주면 됩니다. 마찬가지로 $s_{m2}$를 구하기 위해서는 수신 신호에 $\psi_2(t)$를 곱하고 신호 구간에 대해 적분을 해주면 됩니다.

이를 확장해보자면, ${s_m}$이 orthogonal할 때 $s_{mi} = \int_{0}^{T_b}{r(t)\psi_i(t)dt}$를 이용하여 demodulation을 할 수 있습니다.

Additive White Gaussian Noise (AWGN)

위의 내용들은 noise가 없다는 가정하에 설명한 내용이지만, 실제로는 통신 장비의 열 등으로 인한 열잡음이 발생을 하게 되고, 이를 AWGN이라고 합니다. Additive라는 의미는 이 잡음이 곱해지지 않고 단순히 더해진다는 의미입니다. 그래서 보통 수신 신호를 표현할 때 $r(t) = s_m(t) + n(t)$ 꼴로 사용합니다. White라는 의미는 이 잡음이 주파수 전대역을 포함한다는 것을 의미하고 Gaussian Noise라는 것은 Gaussian 분포를 띄는 random process임을 의미합니다.

AWGN은 기대값이 0이고 correlation이 $R_n(\tau)=\frac{N_0}{2} \delta(\tau)$라는 특징을 갖고 있습니다. 여기서 $N_0$은 noise power spectral density(잡음 스펙트럼 밀도)를 의미하고, $\delta(t)$는 dirac delta function을 의미합니다. 즉, correlation이 $\tau = 0$일 때에는 $\frac{N_0}{2}$, 그 외의 경우에는 모두 0이라고 해석할 수 있습니다.

실제로 전송한 신호에 이 잡음이 더해져서 수신단에 전송되기 때문에 송신 메시지와 수신 메시지가 다를 수 있습니다. 수신된 신호를 제대로 사용하기 위해서 우리는 송신단에서 보낸 신호가 무엇인지 예측을 해야하고, 이 과정에서 당연하게도 에러가 발생할 수 있습니다. 우리의 궁극적인 목표는 이 에러가 발생할 확률을 최소화하는 것이 될 것입니다.

마치며

이번 글에서는 Binary signal과 AWGN 채널에 대해서 알아보았습니다. AWGN이 존재하기 때문에 수신단에서는 받은 신호를 통해 전송한 신호가 무엇인지 판단을 해야합니다. 이를 위해서는 어떤 신호를 받았을 때, 무슨 신호를 송신했다고 판단해야 가장 최적의 결과를 얻는지에 대한 판단이 필요할 것입니다.

다음 글에서는 이 AWGN 채널에 관한 내용을 조금 더 다뤄보고자 합니다. 또한, 이를 위에서 설명했던 binary signal에 적용하여 demodulation 방법과 error가 발생할 확률에 대해 알아보고, 나아가 M-ary, 즉 보내는 정보의 bit 개수가 1개가 아니라 여러 개인 시스템으로 확장해 보겠습니다.

Reference

  • Fundamentals of Communication Systems, John G Proakis