juney's profile image

juney

May 15, 2021 12:00

Connectivity Problem

$k+1$개 이상의 정점을 가진 그래프 $G$가 임의의 $k-1$개의 정점을 제거하더라도 남은 그래프가 connected graph를 유지한다면 그래프 $G$를 k-vertex-connected 라고 합니다. 이때 이를 만족하는 $k$ 중 가장 큰 값을 $G$ 의 vertex connectivity 라고 합니다. 비슷한 방식으로 간선의 경우도 $k-1$개의 간선을 제거하더라도 남은 그래프가 connected graph인 경우 k-edge-connected 라고 표현하고, 그중 가장 큰 $k$ 를 $G$의 edge connectivity 라고 합니다.

아래 그림은 2-vertex-connected 그래프의 예시입니다. 어떤 정점을 삭제하더라도 남은 그래프가 연결 그래프로 유지되기 때문입니다.

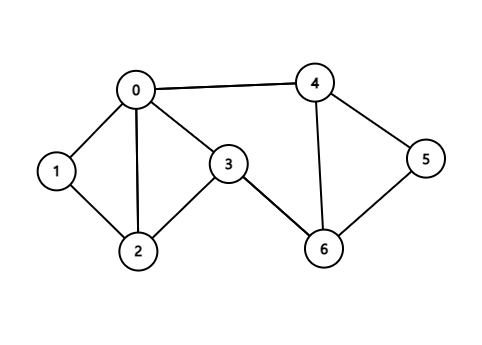
그래프는 현실의 많은 상황 또는 문제를 추상적으로 표현하기에 좋은 도구입니다. 예를 들면 교통 네트워크, 인터넷 네트워크, 전화 네트워크 등 연결 관계가 중요한 상황에서 그래프를 유용하게 사용할 수 있습니다. 이런 상황들에서 connectivity는 어떻게 활용될 수 있을 까요? 교통 네트워크의 경우 특정 지점이 예기치 못하게 사용할 수 없는 상태가 될 수도 있습니다. 하지만 이 교통 네트워크가 2-vertex connected 인 경우, 사용 불가 상태의 지점 하나를 제외한 모든 지점이 서로 연결 되어있다는 사실을 보장 받을 수 있습니다. 물론 사용 불가 상태의 지점이 두 개 이상이 된다면 더 높은 값의 vertex connectivity 을 가져야 연결 상태가 보장이 될 것입니다. 마찬가지로 지점이 아닌 특정 경로가 마비가 된다면 edge connectivity 를 조사해야 할 것입니다.

이처럼 connectivity는 그래프 이론에서 매우 중요한 분야입니다. 이번 글에서는 그 중에서도 가장 단순한 2-connectivity에 초점을 맞추어 중요한 특징들, 그중에서도 2-connectivity를 조사하는 방법에 대해서 소개해보고자 합니다.

2-connectivity

먼저 시작하기에 앞서, 이번 글에서는 vertex-connectivity 에 초점을 맞추어 이야기를 하고자, 2-connectivity 는 2-vertex-connectivity 를 지칭하는 용어로 사용하겠습니다.

그렇다면, 2-connectivity 의 정의를 다시한번 살펴 보겠습니다.

Definition 2.1 어떤 그래프 $G$가 3개 이상의 정점을 가지고 있고, 임의의 정점 하나를 골라서 삭제하더라도 남은 그래프가 연결 그래프인 경우 $G$를 2-connected 라고 한다.

여기서 정점을 삭제한다라는 표현을 명확하게 하기 위해 그래프에서의 몇 가지 연산과 함께 정의를 내려 보겠습니다.

Definition 2.2 어떤 그래프 $G = (V, E) $에 대해서, 다음 그래프들을 $G$로 부터 정의한다.

• Vertex deletion

  $G-v = (V \setminus {v}, {e \in E: v \notin e })$

• Edge deletion

  $G-e = (V, E \setminus {e})$

• Edge addition

  $G+e = (V, E \cup {e})$

• Edge subdivision

  $G\%e = (V \cup {z}, (E \setminus {{x, y}} \cup {{x, z}, {z, y}}) )$

Definition 2.1 에서 언급한 정점을 삭제하는 연산의 경우 Definition 2.2의 vertex deletion을 뜻합니다. 다른 연산들은 이후 내용에서 더 자세히 살펴 보도록 하겠습니다.

2-connectivity equivalent characterization

이번 파트에서는 2-connectivity를 조사하는데 유용한 동치 조건들을 소개하겠습니다.

Theorem 3.1 그래프 $G$가 2-connected 일 조건은 $G$에 속한 어떠한 두 정점을 선택하더라도, 이 두 정점을 포함하는 사이클이 존재할 조건과 동치이다.

Proof. 먼저, $G$에 속한 어떠한 두 정점을 선택하더라도, 이 두 정점을 포함하는 사이클이 존재하는 경우, $G$가 2-connected 임을 보입시다. 이는 다음과 같이 확인할 수 있습니다. 먼저 어떤 두 정점 $x, y$를 선택했을 때, 이를 제외한 정점 하나를 $G$에서 삭제했다고 가정합시다. 이때 $G$에서는 $x, y$를 포함하는 사이클이 무조건 존재하기 때문에, 즉 $x, y$를 잇는 서로 독립적인 경로가 두 개 이상 존재한다는 뜻이므로, 어떤 정점이 하나 삭제된다고 하더라도 이 둘은 이어져 있을 것 입니다. 따라서 남은 그래프도 연결 그래프일 것이므로 $G$는 2-connected입니다.

다음은 역을 증명해봅시다. 2-connected인 경우 임의의 두 정점 $x, y$에 대해서 $G$에 항상 사이클이 하나 이상 존재함을 보이는 것입니다. 이는 $x$와 $y$의 거리에 대한 수학적 귀납법을 진행하여 보일것입니다. $x$와 $y$의 최소 거리는 $d(x, y)$라고 표현하겠습니다.

1. $d(x, y) = 1$인 경우 $x$와 $y$는 어떤 간선 $e$로 연결 되어있다는 뜻입니다. 이때 $G-e \subset G-x, G-e \subset G-y$ 이고, $G$는 2-connected 이기 때문에, $G-e$는 connected graph입니다 ($x$ 또는 $y$를 삭제한 그래프도 connected graph일 것 이므로). 따라서 $x, y$를 잇는 $e$를 제외한 경로가 존재하므로 $G$에서는 $x, y$를 포함하는 사이클이 존재합니다.
2. $k \ge 2$인 $k$에 대해 $d(a, b) < k$ 인 모든 두 정점 $a, b$에 대해선 이 둘을 포함하는 사이클이 존재한다고 가정해 봅시다. 그렇다면 $d(x, y) = k$인 $x, y$를 살펴봅시다. $G$는 connected graph이므로 $x, y$를 잇는 단순 경로 $P$가 존재할 것입니다. $P$상에서 $y$와 인접한 정점 $z$를 봅시다. $d(x, z) = k-1$이므로 가정에 의해 $x, z$를 포함하는 사이클이 존재합니다. 즉, $x, z$를 잇는 서로 독립적인 두 경로 $P_{1}, P_{2}$ 가 존재한다는 것입니다. 이때, $z$를 삭제한다면, $G$는 2-connected도기 때문에 남은 그래프에서도 $x, y$를 잇는 경로 $P’$가 존재할 것입니다. 여기서 $P’$이 $P_{1}, P_{2}$와 가장 마지막으로 공유하는 정점을 $w$라고 합시다. 일반성을 잃지 않고 $w$가 $P_{1}$에 속하는 정점이라고 생각하면, $P_{2}$와 $x$와 $w$를 잇는 $P_{1}$의 일부, 그리고 $w$와 $y$를 잇는 $P’$의 일부는 $x$와 $y$를 포함하는 사이클이 될 것입니다.

따라서 수학적 귀납법에 의해 $G$에서 어떠한 두 정점을 고르더라도, 그 두 정점을 포함하는 사이클이 존재함을 증명했습니다.

Theorem 3.1 덕분에 우리는 어떤 그래프가 2-connected인지 확인 해볼때 그래프 상 모든 두 정점에 대해서 두 정점을 포함하는 사이클이 존재하는지를 확인해보면 됩니다.

다음은 조금 더 재미있는 동치 조건입니다.

Theorem 3.2 그래프 $G$가 2-connected일 조건은 $G$의 subdivision이 2-connected일 조건과 동치이다.

Theorem 3.2를 증명하기에 앞서, 그래프에서의 subdivision이 무엇인지 기억나시나요? Definition 2.2에 설명이 나와 있지만 처음에는 조금 복잡하게 느껴질수도 있습니다. 하지만 자세히 들여다 보면 굉장히 단순한 연산입니다. $G$의 subdivision인 $G \% e$는 한마디로 $G$에 속한 간선 $e$를 두 개의 간선과 그 간선 사이를 잇는 정점 하나로 쪼개어서 만든 그래프입니다. 이를 이해하고 증명으로 넘어가겠습니다.

Proof. 먼저 정점 $v \in V(G)$를 생각해봅시다. $G-v$가 연결 그래프일 조건은 $G\%e-v$가 연결 그래프일 조건과 동치라는 것은 금방 알 수 있습니다. 즉, $G\%e$가 2-connected인 경우, $G$도 2-connected입니다.

역을 증명하기 위해선, $G\%e$에 새롭게 추가된 정점 $z$의 경우만을 확인해보면 됩니다. $G$가 만약 2-connected라고 가정해봅시다. $G\%e$ 에 새롭게 추가된 정점을 $z$라고 할때, 우리는 $G\%e-z$만 연결 그래프인지만 확인하면 될 것 입니다. 하지만 이는 마치 $G-e$와 같으므로, $G-e$가 연결 그래프인지 확인하면 되는데, $G$가 2-connected일 경우 $G-e$가 연결 그래프라는 것은 이미 Theorem 3.1을 증명하는 과정에서 증명했습니다. 따라서 역 또한 증명이 완료됩니다.

2-connected graph synthesis

2-connected graph를 다룰 때, 그 중에서도 특히 2-connected graph의 어떤 성질을 증명할 때 정말 유용하게 쓸 수 있는 정리가 존재합니다. 바로 2-connected graph synthesis라고 불리는 정리입니다.

Theorem 4.1 (2-connected graph synthesis) 그래프 $G$가 2-connected일 조건은 $K_{3}$ (정점이 3개인 완전 그래프) 그래프에 edge subdivision과 edge addition 연산만을 이용하여 $G$를 만들 수 있는 조건과 동치이다.

Proof. 먼저, 2-connected graph에 edge addition을 하여 생성한 그래프는 자명하게도 2-connected graph입니다. 또한 2-connected graph에 edge subdivision을 하여 생성한 그래프가 2-connected인 것은 이미 Theorem 3.2에서 증명했습니다. 따라서 어떤 2-connected graph에서 edge addition 그리고 edge subdivision을 이용하여 생성한 그래프는 2-connected입니다. 그렇다면 이제 어떤 2-connected graph도 $K_{3}$으로 부터 생성할 수 있는지만을 확인하면 됩니다. 하지만 이 부분에 대한 증명은 생략하도록 하겠습니다.

Theorem 4.1은 위에서도 언급했듯이, 2-connected-graph의 어떤 성질을 증명하는데 굉장히 강력한 도구가 될 수 있습니다. 그 이유는 edged addition과 edge subdivision으로 부터 더 작은 2-connected-graph와 연관 관계를 가지게 되므로, 수학적 귀납법을 사용할 수 있게 되기 때문입니다.

예를 들어봅시다. Theorem 3.1을 2-connected graph synthesis를 이용하여 증명해보도록 하겠습니다.

1. $K_{3}$의 경우 Theorem 3.1이 성립함을 직접 확인할 수 있습니다.
2. 그래프 $G$는 2-connected이면서 임의의 두 정점에 대해, 그 두 정점을 포함하는 항상 존재한다고 가정합시다. $G$에 edge addition 또는 edge subdivision을 하더라도 새롭게 만들어진 그래프 또한 임의의 두 정점에 대해 그 두 정점을 포함하는 사이클이 존재한다는 것을 증명해봅시다.
   • (edge addition) $G$의 두 정점 $x, y$를 잇는 간선 $e$를 추가한다고 생각해 봅시다. 이때 $G$에선 귀납적 가정 때문에 이미 $e$를 사용하지 않더라도 $x, y$를 포함하는 사이클이 존재하므로 $G+e$ 또한 $x, y$를 포함하는 사이클이 존재합니다.
   • (edge subdivision) $G$에서 두 정점 $x, y$를 잇는 간선 $e$에 대해 edge subdivision을 진행하여 생긴 정점을 $z$, 그리고 $x, z$를 잇는 간선을 $e_{1}$, $y, z$를 잇는 간선을 $e_{2}$라 합시다. 그럼 $z$를 포함하는 정점 쌍에 대해서만 그 정점 쌍을 포함하는 사이클이 존재하는지 확인하면 됩니다. 즉, 임의의 정점 $v \in G$에 대해서, $z$와 동시에 포함되는 사이클이 항상 존재하는지 확인해보면 됩니다. 먼저 $x$와 $v$사이 사이클을 끝점이 $x, v$인 독립적인 두 경로 $P_{1}, P_{2}$로 나누고, $y$의 경우도 마찬가지 방식으로 $y$와 $v$ 사이 사이클을 $P_{3}$, $P_{4}$로 나눕시다. 여기서 만약 $P_{1}$과 $P_{3}$상에서 겹치는 정점이 $v$로 유일하면 $P_{1}, P_{3}, e_{1}, e_{2}$로 이루어진 사이클은 $z$와 $v$를 지날겁니다. $P_{1}$과 $P_{3}$상에서 겹치는 정점이 $v$로 유일하지 않다면, $P_{1}, P_{3}$이 제일 먼저 만나는 정점을 $w$라고 합시다. 또한 $P_{3}, P_{4}$ 중 $P_{1}$과 제일 먼저 만나는 경로를 일반성을 잃지 않고 $P_{3}$라고 가정합시다. 그러면, $x$부터 $w$까지는 $P_{1}$ 경로, $w$부터 $v$까지는 $P_{3}$의 경로를 취한 새로운 경로를 $P’$라고 하면, $P’, P_{4}, e_{1}, e_{2}$로 이루어진 사이클은 $z$와 $v$를 지날겁니다. 따라서 증명이 완료되었습니다.

마무리

이번 글에서는, 그래프 이론에서 중요한 문제인 connectivity에 관한 소개와 그 중에서도 2-connectivity에 대한 특징들을 집중적으로 알아보았습니다.2-connected일 조건과 동치인 조건들과, 그 중에서도 Theorem 4.1인 2-connected graph synthesis에 대해 배워, 2-connected graph 관련 성질을 증명하는데 유용한 방법에 대해 알게 되었습니다. 이 글을 바탕으로 이후에 k-connectivity 등 더 복잡한 내용에 대해서 공부하는데 필요한 도움이 되었기를 바랍니다.