Multi-Party Computation 2
1. Introduction
저번 시간에 이어서 Multi-Party Computation을 살펴보겠습니다. 저번 시간에는 MPC를 할 수 있는 Garbled Circuit을 만드는 방법을 알아보고 Garbled Circuit이 처음 등장한 1982년부터 Half-gates technique이 발표된 2015년까지 어떠한 흐름을 통해 발전해왔는지 확인했습니다. 이번 시간에는 실제 Garbled Circuit을 구현할 때에는 어떤 방법을 이용하는지, 그리고 그와 관련한 안전성과 공격을 살펴보겠습니다.
2. Half-gates technique
저번 글에서는 이 Half-gates technique에 관해 아주 간략하게 설명을 하고 넘어갔습니다. 그러나 이번 글에서 본격적으로 안전성에 대해 논의를 하다보면 Half-gates technique의 동작에 대해 정확하게 이해할 필요가 있기 때문에 동작 원리를 다시 살펴보겠습니다.
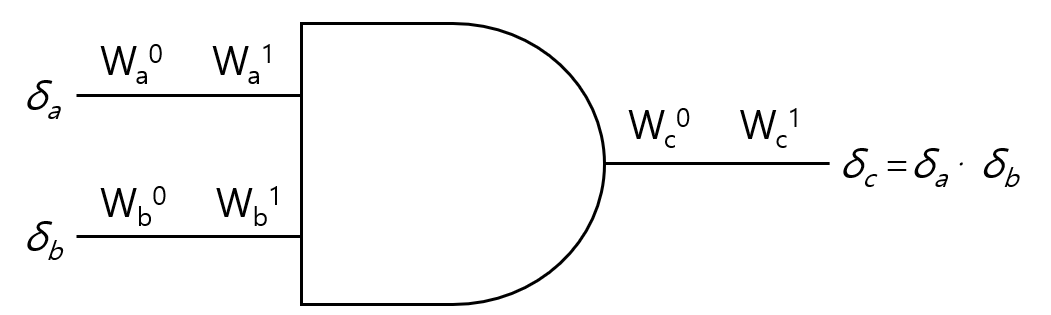
우선 Garbled circuit에서 하나의 AND gate만 놓고 확인을 해보겠습니다. $\delta_a \cdot \delta_b = \delta_c$라는 AND 연산을 수행하고 싶은 상황이고, 이 때 Garbler는 각 wire에 false 값을 나타내는 $W_a^0, W_b^0, W_c^0$과 true 값을 나타내는 $W_a^1, W_b^1, W_c^1$을 정합니다. Free XOR에서 살펴보았듯 Garbler는 global offset $R$($\text{lsb} \ R = 1$)을 정해 $W_a^1 = W_a^0 \oplus R, W_b^1 = W_b^0 \oplus R, W_c^1 = W_c^0 \oplus R$을 만족하도록 합니다. 또한 Evaluator가 넘겨받거나 계산 중에 자연스럽게 알게되는, 해당 wire에 대응되는 값은 $W_a, W_b, W_c$라고 하겠습니다. 이 때 $W_a = W_a^{\delta_a}, W_b = W_b^{\delta_b}, W_c = W_c^{\delta_c}$가 됩니다.
그리고 $p_a$ : $\text{lsb} \ W_a^0$, $s_a$ : $\text{lsb} \ W_a$를 생각해보면 $p_a$는 Garbler가 알고있는 값, $s_a$는 Evaluator가 알고 있는 값입니다.
또한 $\text{lsb} \ W_a^0 \neq \text{lsb} \ W_a^1 (\because \text{lsb} \ R = 1)$임을 생각해보면
-
$p_a = s_a \Rightarrow \text{lsb} \ W_a^0 = \text{lsb} \ W_a \Rightarrow \text{lsb} \ W_a^0 = \text{lsb} \ W_a^{\delta_a} \Rightarrow \delta_a = 0$
-
$p_a \neq s_a \Rightarrow \text{lsb} \ W_a^0 \neq \text{lsb} \ W_a \Rightarrow \text{lsb} \ W_a^0 \neq \text{lsb} \ W_a^{\delta_a} \Rightarrow \delta_a = 1$
이기 때문에 결론적으로 $\delta_a = p_a \oplus s_a$임을 알 수 있습니다.
그러면 이제 어떻게 $\delta_a \cdot \delta_b = \delta_c$를 두 개의 half gate로 나누는지 살펴본다면
$\delta_c = \delta_a \cdot \delta_b$ $\space \space \space \space = \delta_a \cdot (p_b \oplus p_b \oplus \delta_b)$ $\space \space \space \space = (\delta_a \cdot p_b) \oplus (\delta_a \cdot (p_b \oplus \delta_b))$ $\space \space \space \space = (\delta_a \cdot p_b) \oplus (\delta_a \cdot s_b)$
가 됩니다. $\delta_a$는 Garbler, Evaluator 모두 알 수 없는 값인 반면 $p_b$는 Garbler가 알고 있고 $s_b$는 Evaluator가 알고 있습니다.
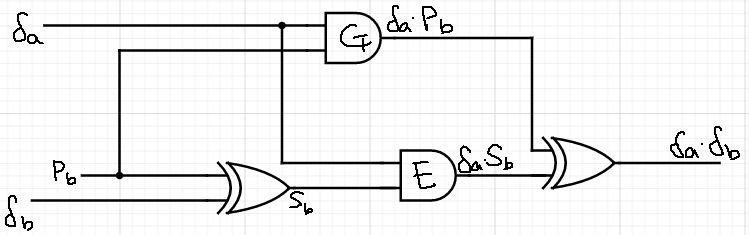
i. Garbler Half-Gates ($\delta_a \cdot p_b$)
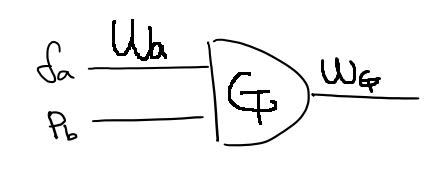
먼저 Garbler Half-Gates를 보겠습니다. 우리는 적절한 $W_G^0, W_G^1$ 값을 정해 Evaluator는 $\delta_a \cdot p_b$ 값에 대응되는 $W_G^0$ 혹은 $W_G^1$을 얻을 수 있게 하고, 한편으로 Evaluator가 자신이 얻은 값이 $W_G^0$인지 $W_G^1$인지는 모르게 해야 합니다.
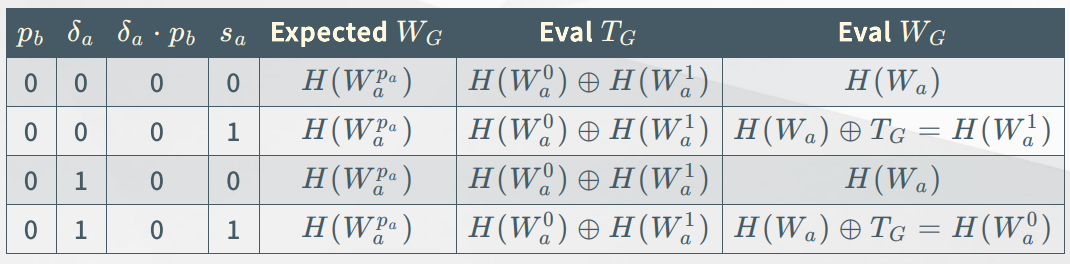
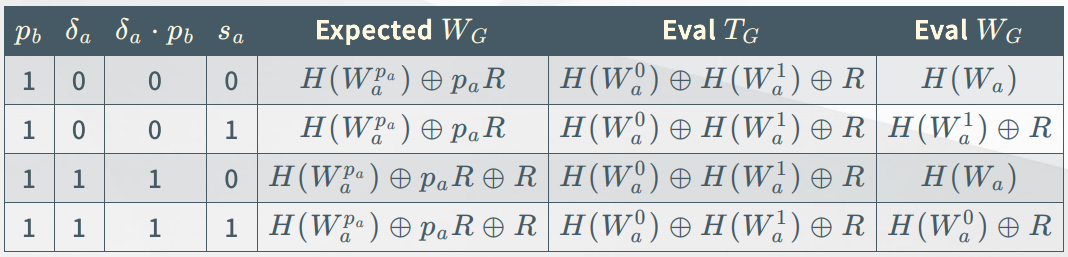
결론적으로 말해 $p_b = 0$일 경우에는 $W_G^0 = H(W_a^{p_a}, j), W_G^1 = W_G^0 \oplus R$으로 두고 $p_b = 1$일 경우에는 $W_G^0 = H(W_a^{p_a}, j) \oplus p_aR, W_G^1 = W_G^0 \oplus R$으로 두면 됩니다. 이 때 $T_G = H(W_a^0, j) \oplus H(W_a^1, j) \oplus p_bR$는 Garbler가 계산한 후 Evaluator에게 줘야하는 값입니다.
Evaluator는 $T_G$를 넘겨받아 $W_G = H(W_a, j) \oplus s_a T_G$를 계산하면 됩니다.
$p_b, \delta_a, s_a$ 각각의 값에 따라 $W_G$가 정말 올바른 값이 되는지는 아래의 테이블로 확인할 수 있습니다.
ii. Evaluator Half-Gates ($\delta_a \cdot s_b$)
다음으로 Evaluator Half-Gates를 보면 마찬가지 논리로 적절한 wire 값 $W_E^0, W_E^1$를 정하고 Evaluator는 Garbler로부터 $T_E$를 넘겨받아 $W_E$를 계산할 수 있습니다.
$p_b = 0$일 때 $W_E^0 = H(W_b^0, j’), W_E^1 = W_E^0 \oplus R$이고 $p_b = 1$일 때 $W_E^0 = H(W_b^1, j’), W_E^1 = W_E^0 \oplus R$입니다. 또한 $T_E = H(W_b^0, j’) \oplus H(W_b^1, j’) \oplus W_a^0$이고 $T_E$를 받은 Evaluator는 $W_E = H(W_b, j’) \oplus s_b(T_E \oplus W_a)$를 통해 $W_E$를 얻을 수 있습니다. 마찬가지로 $s_a, \delta_a, p_b$에 따른 각 값은 아래의 테이블로 제시하겠습니다.


이렇게 Garbler Half-Gates와 Evaluator Half-Gates를 모두 마친 후에는 $W_G \oplus W_E$를 계산해 최종 AND 결과를 알 수 있습니다. Garbled curcuit을 만들 때 AND를 수행하는 부분에 대한 구성은 아래와 같이 나타낼 수 있습니다.
function $\text{GbAnd}(W_a^0, W_b^0, R, \text{gid})$
$\space \space j := 2 \times \text{gid}, j’ := 2 \times \text{gid} + 1$
$\space \space p_a := \text{lsb}(W_a^0), p_b := \text{lsb}(W_b^0)$
$\space \space T_G := H(W_a^0, j) \oplus H(W_a^1, j) \oplus p_bR$
$\space \space T_E := H(W_b^0, j) \oplus H(W_b^1, j) \oplus W_a^0$
$\space \space W_G^0 := H(W_a^0, j) \oplus p_aT_G$
$\space \space W_E^0 := H(W_b^0, j’) \oplus p_b(T_E \oplus W_a^0)$
$\space \space W_c^0 := W_G^0 \oplus W_E^0$
$\space \space$return $((T_G, T_E), W_c^0)$
3. Implementation
이렇게 Half-Gate를 수행하는 방법은 알았는데 막상 이것을 구현하는 것은 또 다른 문제입니다. 일단 Garbled circuit에서 필요로 하는 것은 해싱입니다. 위의 식에서 볼 수 있듯 특정 값의 해싱을 통해 Garbled circuit을 구성할 수 있고 SHA256과 같은 좋은 해시 함수를 사용할 수 있습니다. 그러나 성능을 고려할 때 암호화는 해시보다 상당히 빠릅니다. 더 나아가 암호화에서 만약 키가 고정된다면 키 스케쥴을 매번 새롭게 계산할 필요가 없어지기 때문에 압도적인 성능의 차이가 발생합니다. 대표적인 예시로 AES를 Garbled circuit으로 계산하는 상황을 생각할 때 해시로 구현한 것과 Fixed-key AES를 사용한 것의 성능 차이는 대략 500배 가까이 납니다.
그렇기 때문에 Garbled circuit에 필요한 해시 함수 $H$를 Fixed-key AES로 구현하고자 하는 시도가 있어왔습니다. 단, AES는 Pseudo Random Permutation인 반면 해시 함수는 Pseudo Random Function인 반면 무작정 $H$를 $AES_K$로 대체할 수는 없습니다. 그렇기에 2013년에 소개된 방법은 $H(x, j) = AES_K(2x \oplus j) \oplus 2x \oplus j$로 사용하는 방법입니다.
4. Attack
그러나 $H(x, j) = AES_K(2x \oplus j) \oplus 2x \oplus j$에 대한 공격이 2020년에 발표되었습니다. 이 공격은 AND gate의 개수가 $C$개라고 할 때 $O(2^k/C)$에 동작합니다. Evaluator의 입장에서 공격의 목표는 global shift $R$을 알아내는 것입니다. 만약 $R$을 알아내면 중간 값의 비트를 반전할 수 있고 심지어 최종 결과 또한 조작할 수 있습니다.
공격에서의 핵심은 Half Gates의 과정에서 보았듯 각 AND gate마다 evaluators는 $W_a$와 $T_G = H(W_a^0, j) \oplus H(W_a^1, j) \oplus p_bR$를 알게 됩니다. $H_a = T_G \oplus W_a = H(W_a \oplus R, j) \oplus p_bR$으로 정의할 때 $p_b$는 1/2의 확률로 0이니 곧 1/2의 확률로 $H_a = H(W_a \oplus R, j)$임을 알 수 있습니다.
이렇게 $H_a$들을 수집한 후 임의의 $W_i’$를 잡아 $H(W_i’, 0) = H_a$을 만족하는 $a$가 있는지 확인합니다. 만약 있다면 $2W_i’ = 2(W_a \oplus R) \oplus j$이라는 식을 통해 $R$을 바로 복구할 수 있습니다. $H(W_i’, 0) = H_a$일 때 $2W_i’ = 2(W_a \oplus R) \oplus j$가 확률은 False positive를 계산할 때 대략 1/3이기 때문에 충분히 합리적입니다.
결론적으로 AND gate가 $C$개라고 할 때 대략 $3 \cdot 2^{k+1}/C$개 정도의 $W_i’$ 값을 확인해보면 $R$을 알아낼 수 있습니다.
5. Proposed Hash Function
논문에서는 새로운 구조를 제안하고 다양한 새로운 정의를 제시하며 그 구조에 대한 Concrete Security를 증명하지만 이 증명을 이해하려면 이전에 Provable Security에 충분히 익숙해야하는 관계로 아쉽지만 수식을 이용한 설명은 배제할 계획입니다.
먼저 $\sigma : {0, 1}^L \rightarrow {0, 1}^L$는 아래의 조건을 만족할 때 Linear orthomorphism입니다.
- $\sigma(x \oplus y) = \sigma(x) \oplus \sigma(y)$
- $\sigma$ is a permutation
- $\sigma’(x) = \sigma(x) \oplus x$ is also a permutation
새로운 구조에는 Linear orthomorphism이 쓰이고, 어떤 Linear orthomorphism을 사용해도 상관없지만 실제 구현에는 구현 시 성능이 좋은 $\sigma(x_L | x_R) = x_R \oplus x_L | x_L$이 사용됩니다.
또한 Cipher $E : {0, 1}^L \times {0, 1}^L \rightarrow {0, 1}^L$는 첫 번째 인자가 키이고 두 번째 인자가 평문이라고 생각할 수 있습니다. 각 키에 따라 $E$가 독립적인 Random Permutation이 될 경우 이러한 $E$를 우리는 ideal cipher라고 부릅니다.
최종적으로 우리가 사용할 $H = E(i, \sigma(x)) \oplus \sigma(x)$입니다. 이러한 $H$를 사용했을 때 Garbled circuit은 아래와 같은 advantage를 가집니다. $\mu$는 임의로 정할 수 있는 parameter이고 $u$는 동시에 실행하는 Garbled circuit의 개수, $C$는 AND gate의 수, $p$는 Ideal cipher에 질의할 수 있는 횟수를 나타냅니다.
Garbled circuit은 아래와 같은 advantage를 가진다는 뜻은 공격자의 입장에서 해당 Garbled circuit에서 의미있는 정보를 알아낼 확률이 $\epsilon$ 이하라는 의미입니다.
$\epsilon = \frac{\mu \cdot p + (\mu -1) \cdot C}{2^{k-2}} + \frac{q^{\mu+1}}{(\mu+1)! \cdot 2^{\mu L}}$
식이 복잡한 관계로 실제 수를 대입한 상황을 보면
$k = 80, C \leq 2^{43.5}$일 때에는 $\mu = 1$로 두면 최적이고 이 때 $\epsilon \leq \frac{p}{2^{78}} + 2^{-40}$입니다.
$k = 128, C \leq 2^{61}$일 때에는 $\mu = 2$로 두면 최적이고 이 때 $\epsilon \leq \frac{p}{2^{125}} + 2^{-64}$입니다.
2013년에 제안된 구조에서는 $k = 80, C = 2^{43}$일 때 대략 $2^{37}$번의 질의로 공격에 성공했지만 지금의 구조에서는 $C$의 값과 무관하게 공격에 성공하기 위해서는 $2^{78}$번의 질의가 필요합니다.
이렇게 큰 안전성의 차이가 발생한 이유는 지금의 구조가 Linear orthmorphism을 이용해 최대한 충돌을 회피한 반면 2013년의 구조는 마치 birthday problem과 같이 충돌이 생각보다 높은 확률로 발생할 수 있음에 있습니다.
6. Conclusion
이번 글에서는 Half-gates technique에 대한 자세한 명세와 성능상의 문제로 인해 해시 함수 대신 Fixed-key AES를 사용하는 상황을 설명했습니다. 또한 기존에 제시된 구조의 공격을 알아보고 새로운 구조를 익혔습니다.
새로운 구조의 안전성에 대해 짚어보지 못해서 약간 아쉬움이 있습니다. 이 글의 대부분의 내용은 논문의 내용을 정리한 것이니 관심이 있으신 분은 Better Concrete Security for Half-Gates Garbling 논문을 참고해보시길 권장드립니다.