Indistinguishability in Cryptography
1. Introduction
주어진 암호를 키에 대한 정보 없이 전수 조사보다 더 효율적으로 완전히 해독할 수 있다면 더할 나위 없이 강력한 공격입니다. 특히 현재 널리 쓰이고 있는 암호 시스템에 대해 이러한 공격을 찾았다면 정말 큰 업적을 세웠다고 할 수 있습니다. 그러나 수명, 많게는 수십명이 협력해 만들고 긴 시간을 걸쳐 검증을 받아온 암호 시스템에서 이러한 공격이 발견되기란 굉장히 어려운 일입니다.
이렇게 암호문을 완전히 해독하는건 매우 힘들지만 학계에서는 꼭 암호문을 완전 해독해내는 것이 아닌 더 느슨한 환경에서의 조그만 발견도 의미있는 공격으로 여깁니다. 예를 들어 블록 암호 혹은 해쉬 함수에서 라운드 수를 줄인 시스템에 대한 공격(Reduced-round attack)이나, 키 전체가 아닌 일부 키 비트 복원(Partial key-recovery attack)등을 예로 들 수 있습니다.
심지어는 암호문 결과를 랜덤한 메시지와 구분불가능한지를 따지기도 합니다. 이 성질은 Indistinguishability라고 불리고, 위에서 언급한 모든 공격들이 가능하다는 얘기는 결국 암호문이 어떤 면에서든 편향적인 특성을 가진다는 의미이기 때문에 곧 랜덤한 메시지와 Distinguish가 가능함을 의미합니다. 반대로 말해 암호문이 랜덤한 메시지와 구분불가능하다는 것은 공격자의 입장에서 암호문을 분석하더라도 아무런 의미있는 정보를 얻을 수 없다는 의미이기 때문에 이 성질은 암호문이 안전함을 보장하는 아주 강력한 성질입니다.
Indistinguishability는 달성하기가 굉장히 어려운 성질입니다. 현재 널리 쓰이는 AES, SHA-256 등을 예로 들면 이들은 다양한 공격들로부터 안전하다는 것을 근거로 안전하다고 가정하고 있을 뿐 Indistinguishability를 따로 증명한 것은 아닙니다.
이번 글에서는 Indistinguishability에 대한 관련 이론들을 넓고 얕게 다뤄보고자 합니다.
2. Preliminaries
A. Advantage
암호학에서 Advantage는 Adversary가 두 함수 $F, G$를 구분할 확률을 의미합니다. 아래와 같이 Adversary는 $F$인지 $G$인지 모를 Black box를 받아들고 여기에 원하는대로 질의를 해서 그 결과를 바탕으로 Black box가 $F$인지 $G$인지를 맞춰야 합니다.
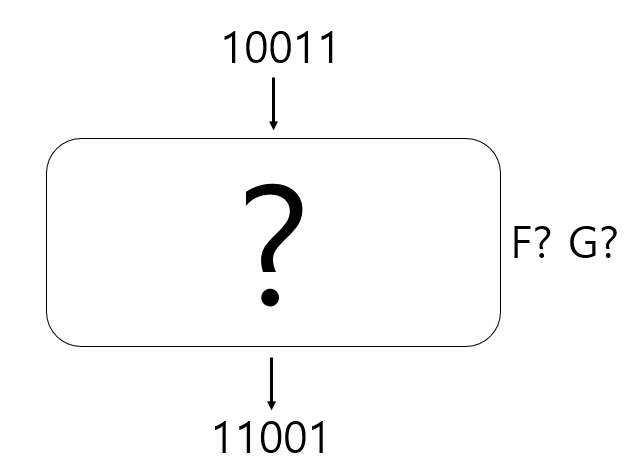
만약 $F$라고 생각할 경우 1이라고 답변할 것이고 $G$라고 경우 0이라고 답변한다고 가정하겠습니다. 이 때 Advantage는 함수가 $F$일 때 이를 $F$라고 판단할 확률에서 $G$일 때 이를 $F$라고 판단할 확률을 뺀 값입다다. 기호로 표현하자면 Adversary $A$의 Advantage는 $Adv(A) = |Pr[A(F) = 1] - PR[A(G) = 1] |$ 입니다. 만약 Adversary가 매번 그냥 동전을 던져 앞면이 나오면 1, 뒷면이 나오면 0이라고 판단한다면 $Pr[A(F) = 1] = 0.5, Pr[A(G) = 1] = 0.5$이기 때문에 Advantage는 0이 됩니다. 반대로 Adversary가 적절한 $F$와 $G$의 특성을 잡아 완벽하게 둘을 구분할 수 있다고 하면 $Pr[A(F) = 1] = 1, Pr[A(G) = 1] = 0$이기 때문에 Advantage는 1이 됩니다. 즉 Advantage는 0에서 1 사이의 값을 가지고 크면 클수록 공격자가 $F$와 $G$를 잘 구분할 수 있음을 의미합니다.
B. PRP(Pseudorandom Permutation)
PRP(Pseudorandom Permutation)는 말 그대로 유사 랜덤 퍼뮤테이션을 의미합니다. mapping $F : {0,1}^n \rightarrow {0,1}^n$을 생각해볼 때 직관적으로는 $F$가 가능한 $2^n!$개의 permutation 중에서 uniformly random으로 선택될 경우 이러한 $F$를 PRP라고 부르고, 수학적으로는 공격자의 입장에서 $F$와 $2^n!$개의 permutation 중에서 uniformly random으로 선택된 $G$를 구분하는 Advantage가 0에 가까울 경우 $F$를 PRP라고 정의합니다.
AES와 같은 대칭키 암호를 생각해보면 암호는 복호화가 가능해야 하므로 Permutation으로 볼 수 있습니다. 또한 비록 수학적으로 증명되지는 않았지만 현재까지 메이저한 취약점이 발견되지 않았기 때문에 키가 고정된 AES는 일종의 PRP로 간주할 수 있습니다. AES는 하드웨어에서 전용 instruction이 존재해 매우 빠르게 수행이 가능한 만큼 PRP가 필요할 경우에는 AES를 사용하는 것이 일반적입니다.
C. PRF(Pseudorandom Function)
PRF(Pseudorandom Function)는 PRP와 다르게 permutation이 아닐 수 있습니다. 각 입력은 임의로 정해진 출력을 반환합니다. mapping $F : {0,1}^n \rightarrow {0,1}^n$을 생각해볼 때 직관적으로는 $F$가 가능한 $(2^n)^{(2^n)}$개의 function 중에서 uniformly random으로 선택될 경우 이러한 $F$를 PRF라고 부르고, 수학적으로는 공격자의 입장에서 $F$와 $(2^n)^{(2^n)}$개의 function 중에서 uniformly random으로 선택된 $G$를 구분하는 Advantage가 0에 가까울 경우 $F$를 PRF라고 정의합니다.
PRF는 해쉬 함수에 대응된다고 생각할 수 있습니다. PRF가 필요할 경우에는 SHA256과 같은 해쉬 함수를 이용하는 것이 일반적입니다.
D. PRP vs PRF
$F, G$를 16비트 입력을 받아 16비트 출력을 하는 함수로 정의하겠습니다. 이 때 $F$는 PRP이고 $G$는 PRF입니다. 이 때 여러 번의 질의를 통해 둘을 구분하려고 하는 알고리즘을 같이 생각해봅시다.
가장 쉽게 떠올릴 수 있는 알고리즘은 $2^{16}$가지의 모든 가능한 입력을 넣어보는 알고리즘입니다. Black box에 $2^{16}$가지의 모든 가능한 입력을 넣었을 때 출력이 $0$에서 $2^{16}-1$이 정확히 1번씩 등장한다면 Black Box가 $F$라고 생각해 1을 반환하고, 그렇지 않을 경우 $G$라고 생각해 0을 반환한다고 생각해봅시다.
이 경우 $Pr[A(F) = 1] = 1$입니다. Black box가 $F$,즉 PRP라면 위에서 제시한 알고리즘은 반드시 1을 반환합니다. 반면 $Pr[A(G) = 1] = (2^n)! / (2^n)^{(2^n)}$입니다. 우연히 PRF의 출력값이 PRP와 같은 상황이 나오면 Black box가 $G$인데도 1을 반환할 수 있기 때문입니다. 물론 그 확률은 굉장히 낮습니다. 최종적으로 위의 알고리즘에서 Adversary의 Advantage는 $1 - (2^n)! / (2^n)^{(2^n)}$입니다. 이 알고리즘은 $2^n$번의 질의를 통해 사실상 1에 가까운 Advantage를 얻었습니다.
그런데 질의를 더 적게 하고도 둘을 구분할 수 있는 방법이 있습니다. 바로 Birthday Paradox를 이용하는 방법입니다. PRP와는 다르게 PRF는 대략 $O(2^{n/2})$번의 질의를 하면 높은 확률로 충돌 쌍이 생깁니다. 이를 이용해 $O(2^{n/2})$번의 질의를 하고 충돌쌍이 생긴다면 PRF, 그렇지 않다면 PRP로 판단하는 알고리즘을 제시한다면 이 또한 상당히 높은 Advantage를 얻을 수 있습니다.
일반적인 두 함수 $F, G$가 동일한 함수가 아니라면 결국 $2^n$번의 질의를 거쳤을 때 둘을 구분할 수 있음은 자명합니다. 그렇다면 Adversary의 입장에서는 질의를 덜 하고도 둘을 구분하고 싶어하고 실제로 PRF와 PRP는 $O(2^{n/2})$번의 질의를 통해 구분 가능합니다. 참고로 PRF와 PRP의 구분의 경우 $O(2^{n/2})$번의 질의가 하한임이 증명되어 있습니다.
3. IND-CPA, RoR-CPA
먼저 CPA는 Chosen-Plaintext Attack, 즉 Adversary가 자신이 원하는 메시지에 대한 암호문을 받을 수 있는 상황을 의미합니다. 이러한 환경에서 Adversary가 의미있는 정보를 획득할 수 있는지를 아래와 같은 방식으로 확인합니다.
A. IND-CPA
IND-CPA에서 IND의 의미는 Indistinguishability를 말합니다. 아래의 상황을 같이 봅시다.
- Adversary는 $M_0, M_1$을 Black box에 보냅니다.
- Black box는 $b \in {0, 1}$을 임의로 정해 $E(M_b)$를 Adversary에게 돌려줍니다.
- Adversary는 받은 암호화된 메시지가 $M_0$을 암호화한 것인지 $M_1$을 암호화한 것인지 맞춰야 합니다.
이 상황에서의 Advantage는 2-A에서 정의한 것과 비슷하게 $b$가 1일 때 $M_1$이라고 판단할 확률에서 $b$가 0일 때 $M_0$이라고 판단할 확률을 뺀 값입니다. 또한 CPA 환경이기 때문에 Adversary는 합리적인 횟수만큼의 암호화 쿼리를 수행할 수 있습니다.
이 정의에 입각해서 생각할 때 IV와 같은 랜덤한 값이 없고 입력이 같으면 늘 동일한 출력을 내는 암호화 알고리즘은 IND-CPA 기준으로 안전하지 않습니다. $M_0$ 혹은 $M_1$에 대한 암호화 결과를 받기만 하면 되기 때문입니다.
B. RoR-CPA
RoR-CPA에서 RoR의 의미는 Real or Random입니다. 아래의 상황을 같이 봅시다.
- Adversary는 $M$을 Black box에 보냅니다.
- Black box는 $M’ \in {0, 1}^{(|M|)}$을 임의로 정해 $E(M)$을 돌려주거나 $E(M’)$을 돌려줍니다.
- Adversary는 받은 암호화된 메시지가 $M$을 암호화한 것인지 $M’$을 암호화한 것인지 맞춰야 합니다.
RoR-CPA에서도 마찬가지로 입력이 같으면 늘 동일한 출력을 내는 암호화 알고리즘은 안전하지 않습니다.
C. IND-CPA vs RoR-CPA
마치 P vs NP에서 NP-Complete 문제들끼리 reduction을 하듯 IND-CPA, RoR-CPA 끼리도 서로간의 reduction이 존재합니다.
먼저 encryption scheme $\Pi$가 IND-CPA secure일 경우 RoR-CPA secure임을 보이겠습니다. 이를 증명하기 위해 대우를 증명할 예정입니다. 즉 RoR-CPA 환경에서 답을 알려주는 oracle이 있을 때 IND-CPA 환경에서의 답을 쉽게 알 수 있음을 보일 것입니다.
- $M_0, M_1$을 임의로 정해 IND-CPA Black box에 보내 $C$를 받습니다.
- RoR-CPA oracle에 $M_0$과 $C$를 보내 $C$가 $M_0$을 암호화한 결과인지 아닌지 알아냅니다.
이와 같이 RoR-CPA oracle이 있다면 IND-CPA 환경에서의 답을 쉽게 알 수 있기에 IND-CPA secure일 경우 RoR-CPA secure입니다.
비슷한 방법을 통해 encryption scheme $\Pi$가 RoR-CPA secure일 경우 IND-CPA secure임을 보일 수도 있습니다. 그렇기 때문에 IND-CPA와 RoR-CPA는 equivalent합니다.
4. Generating PRF
기본적으로 PRP와 PRF는 암호 시스템에 많이 활용됩니다. 당장 AES와 같은 블록 암호를 생각해보더라도 블록 암호 내에서 각 블록을 암호화하는 과정은 deterministic하지만 실제 데이터를 암호화할 땐 CBC나 CTR 모드와 같은 운용 모드가 필요하고, 이 운용 모드에서 IV(Initial Vector)라는 이름의 난수가 필요합니다. 그리고 PRF가 PRP보다 더 경우의 수가 많기 때문에 일반적으로 PRF를 사용했을 때 PRP를 사용했을 때에 비해 Indistinguishability에 도움이 되는 경우가 많습니다.
앞서 설명했듯 PRP는 AES와 같은 암호화 알고리즘을 이용해 만들 수 있는 반면 PRF는 SHA256과 같은 해쉬 함수를 이용해 만들 수 있습니다. 그런데 AES에 비해 SHA256과 같은 해쉬 함수는 많이 느립니다. 그렇기 때문에 PRF를 이용하고자 할 때에는 성능의 문제가 생깁니다.
그렇기 때문에 블록 암호를 이용해 PRF를(혹은 해쉬 함수를) 만들 수 있다면 성능 개선에 큰 도움이 될 것이고, 단순히 블록 암호를 이용한 $x \neq y \Rightarrow F(x) \neq F(y)$인 mapping $F$를 찾는 것에서 그치는 것이 아니라 그것이 실제로 PRF임을 앞에서 제시한 PRF의 수학적 정의에 입각해 증명할 필요가 있습니다.
A. Fixed Input Length
입력의 크기가 고정되어 있을 때에는 다양한 Construction이 존재합니다. $P_1, P_2$ 각각을 서로 다른 $n$-bit permutation이라고 할 때
- $PRF(x) = P_1(x) \oplus P_2(x)$
- $PRF(x) = P_1(0 | x) \oplus P_2(1 | x)$
- $PRF(x) = P_2(P_1(x) \oplus x)$
와 같은 다양한 구조들이 제시되었고 이들은 실제로 $O(2^n)$에 가까운 질의를 거쳐야 adversary가 위의 구조와 PRF를 구분할 수 있음이 증명되어 있습니다.
B. Variable Input Length
크기가 고정되어있지 않을 경우에는 Construction이 어려운 편입니다. 그냥 PRP를 가져와서 사용하더라도 $O(2^{n/2})$번의 질의를 거쳐야 PRF와 구분할 수 있기 때문에 적어도 $O(2^{n/2})$번 보다는 더 많은 질의를 거쳐 구분할 수 있어야 좋은 Construction이라고 할 수 있습니다(이러한 bound를 beyond birthday bound라고 부릅니다).
Beyond birthday bound를 만족하는 구조들로는 3kf9, PMAC+, LightMAC+, mPMAC+ 등이 있습니다. 각각의 상세한 구조와 증명은 생략하겠습니다.
5. Indistinguishability in Public Cryptosystem
지금까지는 모두 대칭키 암호에 대한 얘기였습니다. 그런데 공개키 암호 시스템에서도 마찬가지의 논의가 가능하고, 사실 provable security의 역사를 살펴보면 공개키 암호 시스템에서의 논의가 대칭키 암호 시스템에서보다 먼저였습니다.
공개키 암호 시스템에서는 대칭키 암호 시스템과 다르게 기반 문제를 바탕으로 두고 있는 경우가 많습니다. 예를 들어 RSA는 소인수분해의 어려움을 기반 문제로 두고 Elgamal은 이산 로그 문제의 어려움을 기반 문제로 둡니다. 또한 PQC를 예로 들어보면 SVP(Shortest lattice vector problem) 등의 어려움을 기반 문제로 둡니다. 그렇기 때문에 공개키 암호 시스템에서의 Indistinguishability는 기반 문제로의 reduction을 보이는 방식으로 증명이 진행됩니다. 예를 들어 A라는 암호 시스템이 IND-CPA을 만족하지 않으려면 SVP을 쉽게 해결할 수 있어야 한다. 그러므로 A는 SVP가 어려운 한 안전하다.와 같은 방식입니다.
Probable security라는 개념이 다소 늦게 나온 개념인만큼 초기의 암호 시스템은 reduction을 고려해서 설계가 되어있지 않습니다. RSA의 경우에도 소인수분해가 쉽게 가능하다면 RSA 암호 시스템이 안전하지 않은 것은 아니지만 소인수분해로의 reduction은 발견되지 않았습니다.
반면 최근에 공모가 진행중인 PQC(Post Quantum Cryptosystem)에서는 암호 시스템을 제안할 때 SVP, SIVP 등의 문제로 reduction을 밝혀 IND-CPA 혹은 IND-CCA(Chosen Ciphertext Attacks, 원하는 암호문에 대한 평문을 알 수 있는 환경)을 만족함을 증명합니다.
6. Conclusion
이번 글에서는 다소 중구난방으로 Indistinguishability에 대해 논의를 했습니다. 더 명확한 수식과 함께 제시를 했으면 좋았겠다는 아쉬움이 있지만 그렇게 되면 난이도가 너무 올라가서 대략적인 느낌만 잡는 정도로 만족해야 할 것 같습니다.
이 글을 통해 앞으로 A라는 암호 시스템은 128bit의 안전성을 가진다와 같은 표현을 접했을 때 의미하는 바를 명확하게 받아들일 수 있으면 좋겠습니다.