NP-Complete 게임들과 그 증명

안녕하세요?

우리가 여가 시간에 많이 즐기는 친숙한 여러 게임들, 가령 루빅스 큐브(의 최단거리 찾기), 스도쿠와 같은 고전적인 게임들부터 지뢰찾기, 테트리스, 솔리테어, 팩맨, 슈퍼 마리오, 캔디 크러쉬 사가, 2048, 루빅스 큐브, 쿠키 클리커 등과 같은 게임은 NP-Complete 문제임이 증명되어 있습니다.

이번 글에서는 이러한 게임들을 어떠한 decision problem으로 정의하면, 이러한 문제들이 NP-Complete가 되고 이를 어떻게 증명할지에 대해 알아보겠습니다.

P 문제와 NP 문제

P와 NP, 그리고 NP-Hard와 NP-Complete가 어떠한 것인지는 널리 잘 알려져 있습니다.

멤버십 블로그에서도 기존에 이와 관련한 설명을 작성해주신 많은 글들을 찾아볼 수 있었으니, 위에 대한 엄밀한 설명은 생략하도록 하겠습니다. 아래와 같은 글들을 참고하시면 될 것 같습니다.

P VS NP Question

Karp의 21대 NP-완전 문제

계산 복잡도 위계와 불리언 식

엄밀함을 뺀 아주 이해하기 쉬운 간략한 설명으로 핵심만 정리하면, 아래와 같습니다.

P와 NP 문제는 기본적으로 decision problme를 분류하는 기준 중 하나입니다. decision problem이란, 답이 YES or NO 두 가지 중 하나로 결정되는 문제입니다.

예를 들어 도시 간 비용이 모두 주어졌을 때 외판원 문제로 잘 알려진 “모든 도시들을 단 한 번만 방문하고 원래 시작점으로 돌아오는 최소 비용은 얼마인가?”는 decision problem이 아니지만, 이를 “모든 도시들을 단 한 번만 방문하고 원래 시작점으로 돌아오는 k 이하의 비용이 드는 경로가 있는가?”로 바꾸면 decision problem에 해당하게 됩니다.

P 문제는 다항시간에 해를 찾아낼 수 있는 문제이고, NP문제는 답이 Yes일 때 non deterministic polynomial, 즉 비결정적 알고리즘으로 다항시간 내에 해를 찾아낼 수 있는 문제입니다.

비결정적 알고리즘은 랜덤을 생각하시면 이해하기 편한데, 예를 들어 외판원 문제의 답이 Yes, 즉 k 이하의 비용이 드는 경로가 존재할 때, 모종의 방법으로 비용이 k 이하인 경로가 잘 찾아졌다면 이 경로가 valid한 경로인지 검증하는 것은 다항 시간 내에 가능하므로 위 문제는 NP문제임을 알 수 있습니다.

NP-Hard 문제는 모든 NP문제보다 더 어려운 문제들입니다. 더 어렵다는 것은, 문제 P가 다항시간 내에 문제 Q로 환원가능할 때 P보다 Q가 더 어렵다고 할 수 있습니다.

우리는 모든 NP문제들의 리스트를 알고 있지도 않은데 어떻게 모든 NP문제보다 어려운 문제임을 알 수 있을까요? 놀랍게도, 모든 NP문제를 SAT 문제로 환원 가능하다는 Cook-Levin Theorem이 있습니다. 따라서 SAT 문제는 NP-Hard이고, SAT 문제를 다른 문제로 환원할 수 있으면 해당 문제도 NP-Hard 문제임을 보일 수 있습니다.

우리가 이제부터 증명할, 어떠한 문제가 NP-Hard임을 보일 때도 적절한 NP-Hard 문제가 해당 문제로 환원될 수 있음을 보일 것입니다.

마지막으로 NP-Complete는 NP-Hard이며 동시에 NP에 속하는 문제들입니다.

이제 위에서 언급한 게임들의 NP-Hard를 증명하는 간단한 아이디어들을 살펴보도록 하겠습니다.

이러한 게임들이 NP-Hard임을 증명하는 것은 수학적으로 크게 의미있다고 보기는 힘들 수도 있는데, 이런 식으로 문제를 치환해나갈 수 있다는 점이 꽤나 흥미롭고 재미있습니다.

지뢰찾기

첫 번째로 살펴볼 것은 지뢰찾기입니다.

지뢰찾기의 규칙은 모두가 알듯, 모든 지뢰의 위치를 찾는 것입니다. 지뢰가 아닌 위치를 클릭할 경우 타일이 드러나는데, 이 때 자신과 인접한 8개의 타일에 중 지뢰가 몇 개 있는지가 표시됩니다.

지뢰찾기를 decision problem으로는 아래와 같이 정의할 수 있습니다.

Q. 현재 보드판의 상태가 주어질 때, 모순을 일으키지 않는 지뢰의 구성이 하나 이상 존재하는가?

아래 Fig 1의 왼쪽과 같은 경우 지뢰의 구성이 하나 이상 존재하는 경우이고, 오른쪽의 경우 지뢰의 구성이 불가능합니다. 이 문제가 NP문제임은 적절한 답이 주어지면 이를 다항 시간 내에 확인 가능하므로 자명합니다.

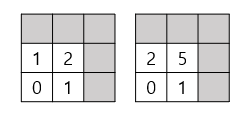
Fig 1. 지뢰찾기의 예시

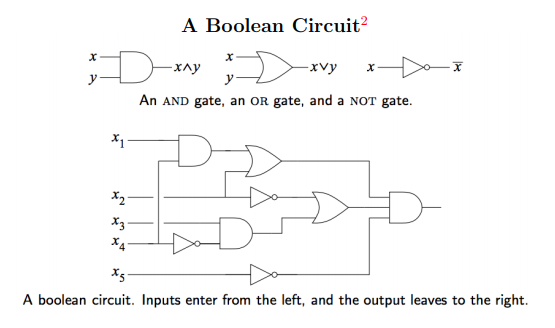
이 문제가 NP-Hard문제임을 어떻게 보일 수 있을까요? 잘 알려진 NP-Hard 문제인 Boolean Circuit 문제를 지뢰찾기 문제로 환원할 수 있습니다.

Boolean Circuit 문제 AND, OR, NOT 게이트와 이들을 잇는 와이어들로 이루어져 있습니다.

Fig 2. Boolean Circuit 문제

재밌게도, 지뢰찾기에서 타일이 적절히 드러나면 각 타일들은 이러한 게이트와 와이어의 역할을 할 수 있습니다.

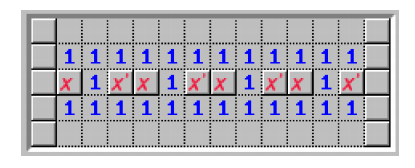
Fig 3. 와이어

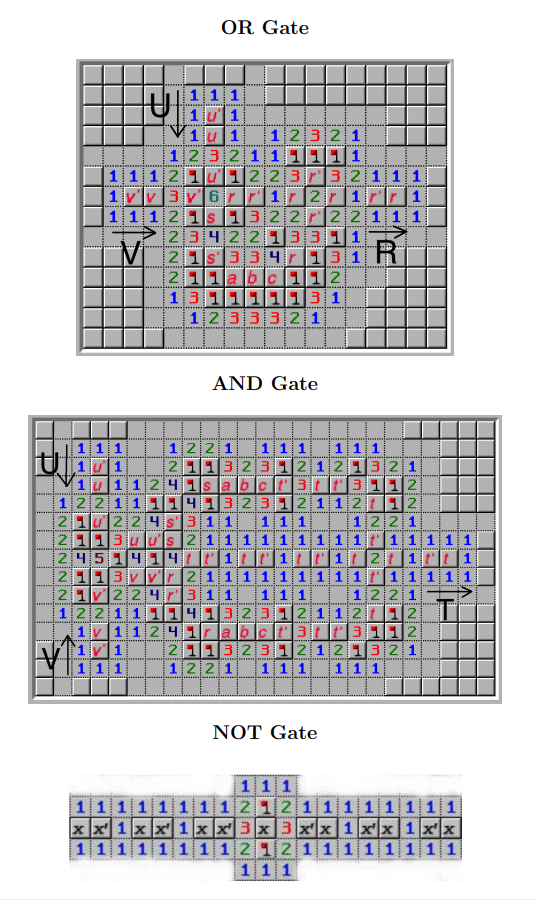
Fig 4. AND, OR, NOT Gate

사진의 출처: http://web.math.ucsb.edu/~padraic/ucsb_2014_15/ccs_problem_solving_w2015/NP3.pdf

와이어와 NOT Gate는 본질적으로 크게 다르지 않지만, 와이어는 항상 3칸씩 움직이게 되는데 이를 조정하는 역할을 해 줄 수 있습니다.

결국, Boolean Circuit는 해당 Circuit의 모양 그대로 지뢰찾기로 옮기는 것이 가능합니다. 따라서 지뢰찾기는 NP-Hard 문제임을 알 수 있습니다.

테트리스

두 번째로 살펴볼 것은 테트리스입니다.

테트리스 또한 아래와 같이 decision problem으로 정의하도록 하겠습니다.

Q. 현재 적절히 쌓여있는 블럭들과 앞으로 들어올 블럭들의 sequence가 주어질 때, 모든 block을 다 없애는 것이 가능한가?

위 문제가 NP문제임은 적절한 정답 움직임이 주어질 경우 다항 시간 내에 확인 가능하므로 자명합니다.

재미있게도 3-partition 문제를 위 테트리스 문제로 환원 가능합니다.

3-partition 문제는 아래와 같습니다.

3s개의 양수가 주어지며, 이 수들의 합은 sT이다. 각 양수들을 $a_1$, $a_2$, …, $a_{3s}$라 하자.
이를 s개의 triplet으로 나누어야 하는데, 이 때 각 triplet에 속한 3개의 양수의 합은 T가 되어야 한다.

조금 더 제약을 둔 버전으로, 아래와 같은 제약을 두어도 문제는 여전히 NP-Hard입니다.

주어지는 모든 양수는 (T/4 , T/2) 범위에 존재한다.

이 문제를 어떻게 테트리스 문제로 바꿀 수 있을까요?

처음에 아래와 같은 모양으로 테트리스가 쌓여있다고 가정해봅시다.

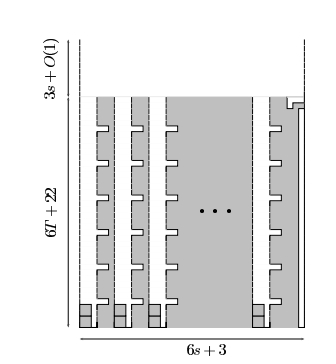
Fig 5. 테트리스 초기 모양

세로로 길게 난 하나의 깊은 구멍마다 하나의 triplet을 할당할 것입니다. 구멍은 총 s개가 있습니다.

이제 블럭들의 sequence가 주어지는데, 아래와 같이 주어집니다.

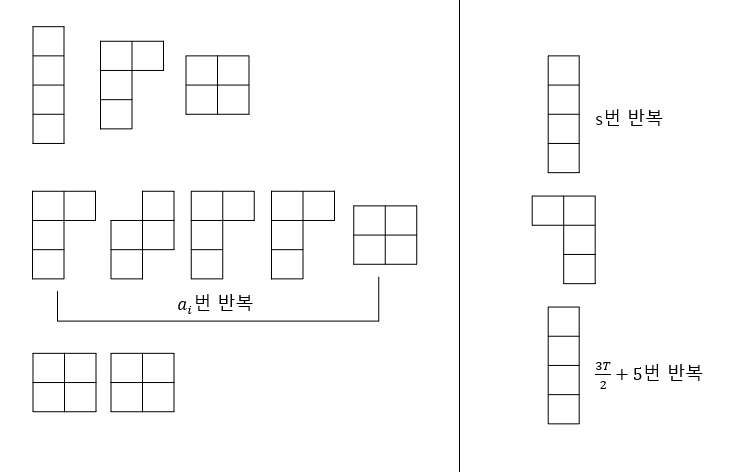
Fig 6. Block들의 sequence

케이스를 많이 따져봐야 하기 때문에 다소 복잡한데, 핵심은 아래와 같습니다.

현재 블럭이 쌓여있는 높이만큼에 있는 빈칸과 sequence로 주어지는 블록이 차지하는 칸의 수가 일치하므로 모든 block은 빈칸 없이 잘 놓여야 합니다.
왼쪽을 막는 위에서 두 번째줄을 제거하기 전까지는 다른 줄을 제거할 수 없으며, 낭비 없이 제거하려면 위에서 두 번째 줄은 오로지 L자 모양의 블럭으로만 제거 가능합니다.
L자 모양 블럭이 주어지기 전까지는 모두 옆에 있는 깊은 구멍에 빈칸 없이 놓여야 합니다.
하나의 빈칸에는 I 모양의 긴 블럭이 먼저 놓여야 다른 것을 빈칸 없이 놓는 것이 가능하며, 이후 블록들은 특정 순서대로만 놓일 수 있습니다.

아래 그림을 통해 조금 더 직관적으로 이해하실 수 있습니다.

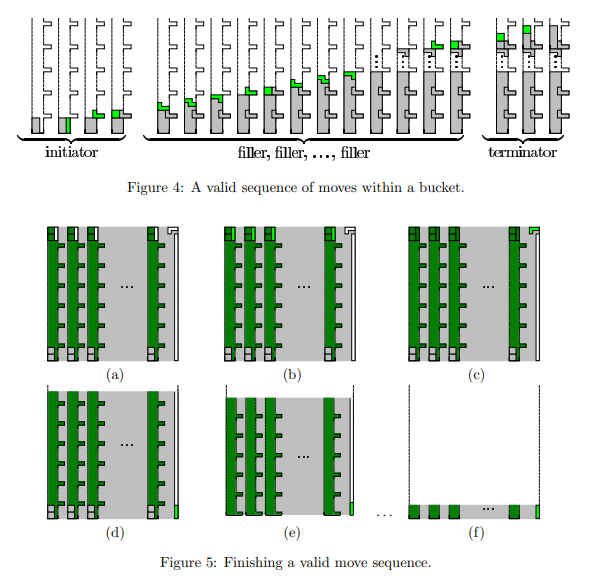
Fig 7. Block들의 가능한 배치

결국 initiator에서 terminator까지의 세트는 하나의 구멍에 들어갈 수밖에 없으며, 모든 수는 (T/4 , T/2) 범위에 존재하므로 3개 들어가면 구멍은 가득차게 됩니다. 하나의 세트는 하나의 수 $a_i$를 나타내므로 결국 어떠한 구멍에 어떤 순서대로 넣는지가 3-partition 문제의 해법을 나타내게 됩니다.

따라서 테트리스 또한 NP-Hard 문제임을 알 수 있습니다.

슈퍼 마리오 브라더스

세 번째로 살펴볼 것은 슈퍼 마리오 브라더스입니다.

슈퍼 마리오 브라더스의 decision problem은 아래와 같이 설정하겠습니다.

Q. 슈퍼 마리오의 골인지점이 출발점으로부터 도달 가능한가?

아주 간단해 보이는 위 질문이 NP-Hard 문제입니다. 이는 슈퍼마리오가 가지고 있는 특성 때문입니다.

캐릭터는 마리오, 슈퍼 마리오 두 가지의 상태를 가지고 있는데 각 상태의 특징은 아래와 같습니다.

마리오: 크기가 1. 벽돌 부수기 x. 버섯을 먹으면 슈퍼 마리오가 된다. 슈퍼 마리오: 크기가 2 (크기가 1인 지점을 지나지 못한다). 벽돌 부수기 o.

만약 위 슈퍼마리오 문제를 푼다면, 3-SAT 문제를 해결할 수 있습니다! 슈퍼마리오는 여러 개의 맵들로 이루어져 있으며, 하나의 맵에서 상/하/좌/우로 이동하면 다른 맵이 나오게 됩니다.

이제 3-SAT의 상황을 아래와 같은 맵들의 배열로 설정할 수 있습니다.

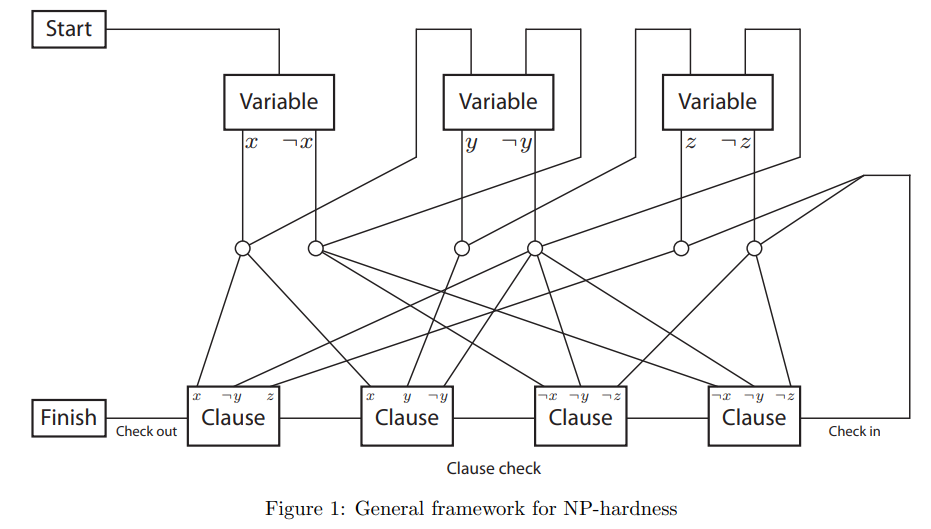
Fig 8. 맵의 배치를 3-SAT으로

Variable은 x 또는 not x 중 하나를 고르는 것을 뜻합니다.

Fig 9. 슈퍼 마리오의 Variable화

위와 같은 맵에서, 슈퍼마리오는 무조건 떨어져야 하고 떨어지면 다시 올라올 수 없으므로 둘 중 하나의 구멍으로 들어가야 합니다. 따라서 x 또는 not x 중 하나를 고르게 됩니다.

다음은 Clause입니다. 아래와 같은 맵에서, 하나 이상의 아이템 상자에서 별 아이템을 획득해야 옆에 있는 불구덩이(?)를 지나칠 수 있으므로, 아래와 같이 맵을 배치하고 각각의 변수와 맵을 잘 이어주면 이는 Clause, 즉 or로 묶인 하나의 쌍을 의미하게 됩니다.

Fig 10. 슈퍼 마리오의 Clause화

마지막은 crossover입니다.

Fig 11. 슈퍼 마리오의 Crossover화

왼쪽에서 진입했을 경우, 지나가기 위해 독버섯한테 한 대 맞고 작아진 채로 지나가서, 오른쪽으로 넘어가 버섯 아이템을 먹고 상자를 부수는 것이 유일한 탈출구입니다. 반대로 아래쪽에서 진입했을 경우, 벽돌을 잘 부수어 위쪽으로 나가는 것이 유일한 탈출구입니다. 따라서 이 맵은 적절한 crossover 상황을 표현 가능합니다.

따라서 주어진 3-SAT 문제를 Fig 8과 같이 적절한 맵의 배치로 바꾸고, 위 맵들을 슈퍼마리오 맵으로 바꾸면 결국 3-SAT 문제가 슈퍼마리오의 골인지점 도달 가능성 문제로 환원됩니다.

팩맨

마지막으로 살펴볼 것은 팩맨입니다. 팩맨의 규칙은, 팩맨이 유령을 피해 작은 점들을 모두 먹으면 게임이 끝나며 중간중간 놓인 큰 점을 먹으면 잠시동안 유령을 겁먹은 상태로 만들 수 있습니다.

팩맨의 decision problem은 아래와 같습니다.

Q. 주어진 맵에서 팩맨이 모든 작은 점들을 먹을 수 있는가?

팩맨은 정말로 간단합니다.

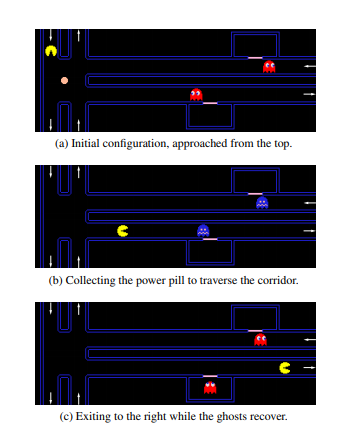
Fig 12. 팩맨의 트릭

아래와 같이 맵을 구성하면, 반드시 공을 먹어야만 팩맨이 길을 지나갈 수 있는 상황이 발생합니다. 공과 함께 적절한 작은 점들이 있다면, 공을 해밀턴 경로가 되도록 순서대로 먹어야 합니다. 따라서 해밀턴 경로 문제를 팩맨 문제로 치환 가능합니다.

마치며

위 문제들은 결국 주어진 게임을 다항식의 범위 내에서 크기를 매우 키운 후 “아주 특이한” 구성을 만들어서 기존의 NP-Hard 문제를 해당 게임의 문제가 되도록 잘 바꾸어, 위 문제들이 NP-Hard 문제임을 증명하고 있습니다. 생각보다 맥이 빠지는 증명들입니다. 하지만 재미있는 아이디어를 살펴볼 수 있어, 많은 영감을 주는 증명들이라고 생각하며 글을 마치겠습니다.

읽어주셔서 감사합니다.