blisstoner's profile image

blisstoner

December 20, 2020 23:30

1. Introduction

저번 글에서는 양자 컴퓨터와 Post Quantum Cryptography에 대해 다루었습니다. 이번 포스팅에서는 어떤 암호 시스템을 다루어볼까 고민하다가 NIST에서 진행하는 PQC contest의 3라운드 7개의 후보 중에서 5개가 Lattice-based인 만큼 Lattice를 기반 문제로 사용하는 SABER 암호의 동작 원리, 장단점을 소개해보려고 합니다.

저도 불과 한달 전까지만 해도 PQC에서 사용하는 Lattice에 대해 아주 얕은 지식만을 가지고 있었기 때문에 Lattice를 잘 모르더라도 글을 이해하는데 큰 어려움은 없습니다. 다만 Group Theory가 많이 쓰이기 때문에 Group Theory에 대한 이해가 약하시면 내용을 따라가는게 많이 힘들 것입니다.

2. Preliminaries

알고리즘을 설명하기 전에 notation과 기본적인 Lattice에 대한 지식을 짚고 가겠습니다. 이 글에서 쓰는 notation은 실제 SABER의 제작자들이 공식 문서에서 사용한 notation을 그대로 따라갑니다.(공식 문서 링크)

Notation

우선 $\mathbb{Z}q$는 ${0, 1, 2, \dots, q-1}$에서 $+, \times$로 정의된 group을 의미합니다. 또한 $R_q = \mathbb{Z}_q[X]/(X^n+1)$입니다. $R_q$를 풀어서 설명하면 $a{n-1} \cdot X^{n-1} + a_{n-2} \cdot X^{n-2} + \dots + a_{1} \cdot X^{1} + a_{0} \cdot X^{0}$이고 $a_i \in \mathbb{Z}_q$, 즉 $0 \leq a_i \leq q-1$입니다. 참고로 SABER에서는 $n = 256, q = 2^{13}$을 사용합니다. $\mathcal{U}$는 Uniform distribution을 의미합니다.

다음으로 $\beta_\mu$는 parameter $\mu$에 대한 Centered binomial distribution을 의미합니다. Centered binomial distribution은 $P[x] = \frac{\mu!}{(\mu/2+x)!(\mu/2-x)!}2^{-\mu}$ for $-\mu/2 \leq x \leq \mu/2$으로 정의되는 distribution입니다. 더 쉽게 설명하면 ($\mu/2$번 동전을 던져 앞면이 나온 횟수) - ($\mu/2$번 동전을 던져 앞면이 나온 횟수)를 분포로 이용하는 distribution입니다. 이 distribution을 사용하는 이유는 분포가 normal distribution과 유사하면서도 값을 계산하기가 굉장히 쉽기 때문입니다.

그 다음으로 $\lfloor x \rceil$은 $x$와 가장 가까운 정수, 즉 반올림을 의미합니다. 보통 $\lfloor x \rfloor$ 혹은 $\lceil x \rceil$이 익숙할텐데 반올림을 $\lfloor x \rceil$으로 나타내는건 저도 처음 알았습니다.

위에서 $R_q$를 소개했는데, 특별히 public key는 $R_p(p = 2^{10})$, ciphertext는 $R_T(T = 2^4)$의 원소로 정의되고 나머지 모든 연산은 $R_q(q = 2^{13})$ 위에서 이루어집니다.

또한 $p < q$일 때 $\lfloor x \rceil_p$은 $\lfloor (p/q) \cdot x \rceil \mod p$으로 정의됩니다. ($x \in \mathbb{Z}q$) 위에서 언급했듯 $p = 2^{10}, q = 2^{13}$이기 때문에 사실 $\lfloor x \rceil_p$은 3비트 내림을 한 후 반올림을 하는 연산입니다. 예를 들어 $\lfloor 110011{2} \rceil_p = 1102, \lfloor 10110{2} \rceil_p = 112$입니다. 그리고 더 나아가 이를 편하게 계산하려면 $\lfloor x \rceil_p = \lfloor (x + 100{2}) \gg 3 \rfloor$입니다. 우리가 어떤 수를 1의 자리에서 반올림한 결과를 알아내고 싶을 때 0.5를 더한 후 버림을 하면 되는 것과 똑같은 원리입니다.

이렇게 $\lfloor x \rceil_p$는 적절한 상수를 더하고 right shift를 수행해서 쉽게 계산이 가능하고 4. Algorithm에서는 $\lfloor x \rceil_p$이라고 쓰는 대신 $\bm{b} = ((\bm{A}^T\bm{s}+\bm{h}) \mod q) \gg (\epsilon_q - \epsilon_p) \in R^{l \times 1}_p$와 같이 굉장히 자연스럽게 적절한 상수를 더하고 right shift를 수행하는 연산으로 나타내기 때문에 나중에 이를 보더라도 당황하지 말아주세요.

위에서 $p, q, r$의 값들에 대해 언급했는데 $p = 2^{\epsilon_p}, q = 2^{\epsilon_q}, T = 2^{\epsilon_t}$으로 $\epsilon_p, \epsilon_q, \epsilon_t$가 정의됩니다. 즉 \epsilon_p = 10, \epsilon_q = 13, \epsilon_t = 4$입니다.

상수 $h_1 \in R_q$은 각 계수가 $2^{\epsilon_q - \epsilon_p - 1} = 2^2$인 다항식을, $h_2 \in R_q$은 각 계수가 $(2^{\epsilon_p-2} - 2^{\epsilon_p - \epsilon_t - 2}) = 2^8 - 2^2$인 다항식을 의미합니다. 나중에 알고리즘을 보면 알겠지만 이 두 상수는 $\lfloor x \rceil_p$을 효율적으로 구현하기 위해 쓰입니다.

기호 $x \leftarrow \chi$는 $x \in S$ probability distribution $\chi$에 따라 선택했다는 의미입니다.

마지막으로 $bits(x, i, j)$는 $(j \leq i)$: $(x \gg (i-j)) \& (2^j - 1)$를 의미합니다. 말로 풀어서 설명하면 LSB $i - j + 1$번째 비트부터 $i$번째 비트까지 총 $j$개의 비트를 뽑는 함수입니다.

LWE(Learning With Error)

저번 글에서도 아주 간단하게 소개하고 넘어갔지만 다시 한 번 설명하겠습니다. Lattice에서 LWE란 $(\bm{a},b = \bm{a}^T\bm{s} + e)$과 $(\bm{a}, u) \leftarrow \mathcal{U}(\mathbb{Z}^{l \times 1}q \times \mathbb{Z}_q)$이 구분되기 어렵다는 성질을 의미합니다. 여기서 $\bm{s}$는 고정된 secret vector를 의미하고 $\bm{s} \leftarrow \beta\mu(\mathbb{Z}^{l \times 1}q)$으로 정해집니다. 그리고 $e \leftarrow \beta\mu(\mathbb{Z}_q)$는 small error를 의미합니다.

갑자기 기호가 엄청 쏟아져서 당황스럽겠지만 당황할 필요는 없습니다. 저번 글에서 언급한 것과 똑같이 $\bm{a}$가 주어졌을 때 $\bm{a}^T\bm{s}$를 계산하고 small error $e$를 더하면 이를 보고 $\bm{s}$를 복원하기는 어렵다는 의미입니다.

LWR(Learning With Rounding)

SABER에서는 LWE에서 조금 더 발전된 형태인 LWR이라는 개념이 등장합니다. LWR에서는 $(\bm{a}, b = \lfloor \frac{p}{q}(\bm{a}^T\bm{s} ) \rceil ) \in \mathbb{Z}^{l \times 1}_q \times \mathbb{Z}_p$과 $(\bm{a}, u) \leftarrow \mathcal{U}(\mathbb{Z}^{l \times 1}_q \times \mathbb{Z}_p)$이 구분되기 어렵다는 성질을 이용합니다.

Notation에서 $\lfloor (p/q) \cdot x \rceil \mod p$을 하위 3비트 내림 후 반올림을 하는 연산이라는 얘기를 했습니다. 이를 인지하고 다시 위의 식을 보면 LWE에서는 small error를 더해서 $\bm{a}^T\bm{s}$에 약간의 변화를 주는 반면 LWR에서는 하위 3비트 내림 후 반올림을 하는 방식으로 약간의 변화를 준다는 사실을 알 수 있습니다.

LWE와 비교했을 때 LWR의 가장 큰 특징은 LWE와는 달리 small random error $e$가 필요없다는 점입니다. 즉 deterministic한 방식으로 값이 계산되기 때문에 최적화를 할 때 더 유리합니다.

Mod-LWE, Mod-LWR

Mod-LWE, Mod-LWR에서 Mod는 Modulus가 아니라 Module입니다. 위의 LWE, LWR에서 $\mathbb{Z}_q$을 $R_q = \mathbb{Z}_q[X]/(X^n+1)$으로 바꾸면 그것이 바로 Mod-LWE, Mod-LWR입니다.

예를 들어 연산의 단위가 768 bit일 때 LWE에서는 $\bm{a}^T = [a_0, a_1, \dots , a_{767}] (a_i \in \mathbb{Z}_q), e \in \mathbb{Z}_q$으로 사용할 것입니다. 반면 Mod-LWE에서는 $\bm{a}^T = [\tilde{a_0}, \tilde{a_1}, \tilde{a_2}], \tilde{a_i} \in R_q(= \mathbb{Z}_q[X]/(X^n+1)), \tilde{e} \in R_q$으로 사용할 것입니다($n = 256$). LWE/LWR과는 달리 Mod-LWE/Mod-LWR는 256 bit 단위의 블럭 3개로 생각해서 연산을 수행할 수 있어서 소프트웨어 혹은 하드웨어 단위의 최적화에서 이득을 볼 수 있습니다.

3. Key Exchange

드디어 필요한 배경지식을 모두 익혔습니다. 먼저 SABER에서의 Key Exchange를 다루기 전에 ElGamal Encryption과 Diffie-Hellman Key Exchange의 관계를 살펴보겠습니다.

Diffie-Hellman Key Exchange는 아마 이 글을 중간에 나가시지 않고 지금까지 읽고 계신 분이라면 다 알고 계실 개념이라고 생각합니다. Alice와 Bob이 미리 Group $G$와 Generator $g$를 정의한 후 각각 비밀값 $a, b$를 생성해서 $g^a, g^b$를 공유하면 Alice와 Bob은 둘 사이의 통신에서 사용할 비밀키 $g^{ab}$를 알 수 있습니다.

아마 ElGamal Encryption도 아시는 분이 많으실 것 같은데, ElGamal Encryption은 아래와 같은 절차를 통해 진행됩니다.

• Public key = $(G, q, g, h = g^x)$, Private key = $x$

• Encryption : $\text{Enc}(M) = (c_1, c_2) = (g^y, m \cdot h^y)$

• Decryption : $\text{Dec}(c_1, c_2) = (c_1^x)^{-1} \cdot c_2$

Encryption, Decryption이 잘 동작하는지는 간단한 계산으로 쉽게 검증이 가능하고, ElGamal Encryption에서 이해를 하고 가야할 가장 중요한 정보는 ElGamal이 Diffie-Hellman을 바탕으로 만들어졌다는 사실입니다. Diffie-Hellman에서는 Alice와 Bob이 각자의 비밀값 $a, b$를 가지고 비밀키를 생성했다면 ElGamal에서는 $a, b$에 대응되는 $x, y$를 볼 때 $x$가 비밀키로, $y$가 Encryption에서의 난수로 쓰였습니다.

SABER에서도 우선 Key Exchange를 먼저 설명드릴 것이고 이 Key Exchange를 바탕으로 암호화와 복호화가 이루어짐을 이해하시면 되겠습니다.

우선 Key Exchange의 전체 과정은 아래와 같이 상당히 복잡합니다.

저도 맨 처음에 공식 문서를 볼 떄 이 난해한 과정을 보고 대체 어디서부터 어떻게 이해를 해야하나 굉장히 당혹했었습니다. 한참동안 고생하다가 다행히 제작진에서 만든 쉬운 설명 자료를 보고 도움을 얻을 수 있었습니다.

더 쉬운 Key Exchange 설명 그림을 보겠습니다.

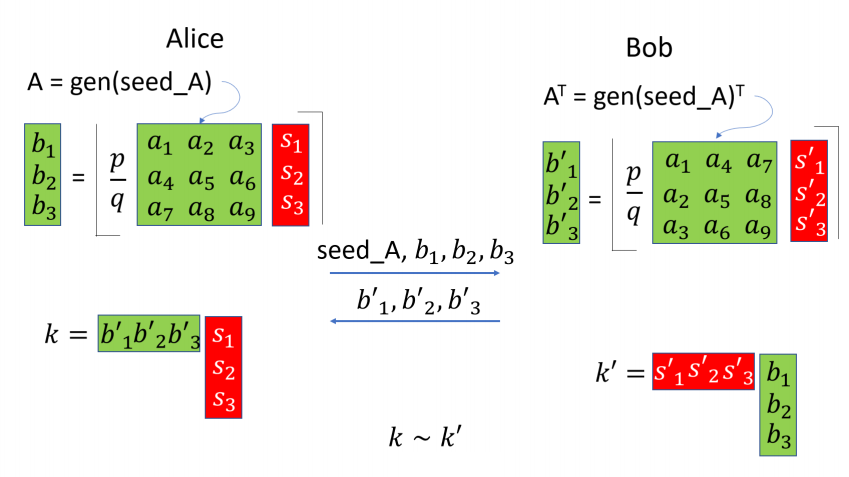
가슴이 웅장해집니다. 여기서 $a_i, b_i, s_i$ 각각은 256차 다항식입니다. $\lfloor \rceil_p$ 연산이 없을 경우 $k, k’$은 동일한 값을 가짐을 알 수 있고 $\lfloor \rceil_p$으로 인해 약간의 오차는 있을 수 있겠지만 대략적인 계산의 흐름은 이해할 수 있을 것입니다.

Diffie-Hellman에서는 $g^x$로부터 $x$를 알기 어렵다는 성질이 쓰인 것 처럼 SABER의 키 교환에서는 $\lfloor \frac{p}{q}(\bm{a}^T\bm{s} ) \rceil$으로부터 $s$를 알기 어렵다는 성질이 쓰입니다.

전체 과정을 잘게 풀어서 설명드리고 싶지만 반드시 필요한 내용이라고는 생각되어지지 않아 이정도로만 이해한채로 Key Exchange 과정을 넘어가겠습니다.

4. Algorithms

이제 드디어 SABER의 각 알고리즘을 소개할 수 있게 되었습니다.

Saber.PKE.KeyGen()

첫 번째로 KeyGen 알고리즘입니다.

1.ㅤ$seed_{\bm{A}} \leftarrow \mathcal{U}({0,1}^{256})$

2.ㅤ$\bm{A} = \text{gen}(seed_{\bm{A}}) \in R^{l \times l}_q$

3.ㅤ$r = \mathcal{U}({0,1}^{256})$

4.ㅤ$\bm{s} = \beta_\mu(R^{l \times 1}_q; r)$

5.ㅤ$\bm{b} = ((\bm{A}^T\bm{s}+\bm{h}) \mod q) \gg (\epsilon_q - \epsilon_p) \in R^{l \times 1}_p$

6.ㅤ$\text{return} \ (pk := (seed_{\bm{A}}, \bm{b}), \bm{s})$

처음 보면 조금 헷갈릴 수 있지만 ElGamal Encryption에서 Public key = $(G, q, g, h = g^x)$, Private key = $x$였다는 사실을 잘 생각하고 다시 봅시다.

Diffie-Hellman에서 $x$와 $g^x$의 관계가 SABER에서 $\bm{s}$와 $\bm{b} = \lfloor \frac{p}{q}(\bm{a}^T\bm{s} ) \rceil$입니다. 그리고 5번에서 $\bm{b}$를 처음 보는 식으로 계산한 이유는 $\lfloor \frac{p}{q}(\bm{a}^T\bm{s} ) \rceil = ((\bm{A}^T\bm{s}+\bm{h}) \mod q) \gg (\epsilon_q - \epsilon_p)$이기 때문입니다. 식이 익숙하지 않으면 그냥 $\bm{b}$를 지금 이해하고 있는 그 방식대로 계산한다고 생각하시면 됩니다.

또한 $seed_{\bm{A}}$는 $\bm{A}$를 만들어내기 위한 값입니다. $\bm{A}$를 직접 주고받는 대신 256비트 seed만 주고받는 것이 효율적이기 때문에 seed를 사용합니다.

그러면 $(seed_{\bm{A}}, \bm{b})$가 Public key이고 $\bm{s}$가 Private key인 것이 이해가 가실 것으로 생각합니다.

Saber.PKE.Enc($pk := (seed_{\bm{A}}), m \in R_2; r$)

다음은 암호화 알고리즘입니다.

1.ㅤ$\bm{A} = \text{gen}(seed_{\bm{A}}) \in R^{l \times l}_q$

2.ㅤ$\text{if} \ r \ is \ not \ specified \ \text{then} \ r = \mathcal{U}({0,1}^{256}$

3.ㅤ$\bm{s}’ = \beta_\mu(R^{l \times 1}_q; r)$

4.ㅤ$\bm{b}’ = ((\bm{A}^T\bm{s}+\bm{h}) \mod q) \gg (\epsilon_q - \epsilon_p) \in R^{l \times 1}_p$

5.ㅤ$v’ = \bm{b}^T(\bm{s}’ \mod p) \in R_p$

6.ㅤ$c_m = (v’ + h_1 - 2^{\epsilon_p - 1}m \mod p) \gg (\epsilon_p - \epsilon_t) \in R_T$

7.ㅤ$\text{return} \ c := (c_m, \bm{b’})$

우선 $r$은 optional argument입니다. 2번에서 보듯 정해져있지 않다면 랜덤으로 정해버리니 크게 의미를 부여할 필요는 없습니다.

5번에서 $v’$이 Diffie-Hellman에서의 비밀키 혹은 SABER 쉬운 버전에서의 $k, k’$과 동일한 값입니다. 즉 $c_m$은 $v’$에서 $m$과 관련된 값을 뺀 값이라고 할 수 있습니다.

Saber.PKE.Enc($pk := (seed_{\bm{A}}), m \in R_2; r$)

다음은 복호화 알고리즘입니다.

1.ㅤ$v = \bm{b}^T(\bm{s}’ \mod p) \in R_p$

2.ㅤ$m’ = ((v - 2^{\epsilon_p - \epsilon_T}c_m + h_2) \mod p \gg (\epsilon_p - 1) \in R_2$

3.ㅤ$\text{return} \ m’$

비밀키를 알고 있으면 $v = v’$을 계산할 수 있고, $v$와 $v’$을 상쇄시켜 $m’$을 복원합니다.

KEM(Key Encapsulation Mechanism)

이 글의 제목이 SABER: Mod-LWR based KEM이었다는걸 인지하고 계셨나요? 아마 KEM이라는 용어를 처음 본 분이 많을 것으로 예상됩니다. KEM은 public-key algorithm을 이용해 shared key를 만들어내는 알고리즘입니다. 여기까지만 설명을 보면 그냥 Diffie-Hellman 키 교환과 다를게 없다고 생각할 수 있지만 KEM은 DH key exchange와 비교할 때 shared key를 한 방향으로 만들어낼 수 있다는 장점이 있습니다.

DH에서는 Alice와 Bob이 모두 비밀값 $a, b$를 생성해서 서로 정보를 주고 받는 과정이 필요합니다. 반면 KEM에서는 Alice가 자신의 Public Key를 공개해둔 후 Bob이 단방향으로 shared key를 만들어낼 수 있습니다.

SABER뿐만 아니라 다른 모든 Round 3의 Public key encryption 알고리즘은 KEM을 포함하고 있습니다.

Saber.KEM.KeyGen()

1.ㅤ$(seed_{\bm{A}}, \bm{b}, \bm{s}) = \text{Saber.PKE.KeyGen()}$

2.ㅤ$pk = (seed_{\bm{A}}, \bm{b})$

3.ㅤ$pkh = \mathcal{F}(pk)$

4.ㅤ$z = \mathcal{U}({0,1}^{256})$

5.ㅤ$\text{return} \ pk = (seed_{\bm{A}}, \bm{b}), sk = (z, pkh, pk, \bm{s})$

이 때 $\mathcal{H}, \mathcal{F}$ : SHA3-256, $\mathcal{G}$ : SHA3-512입니다.

이 KEM의 KeyGen은 Alice가 수행합니다.

Saber.KEM.Encaps($pk = (seed_{\bm{A}}, \bm{b})$)

1.ㅤ$m = \mathcal{U}({0,1}^{256})$

2.ㅤ$(\hat{K}, r) = \mathcal{G}(\mathcal{F}(pk), m)$

3.ㅤ$c = \text{Saber.PKE.Enc}(pk,m;r)$

4.ㅤ$K = \mathcal{H}(\hat{K}, c)$

5.ㅤ$\text{return} \ (c, K)$

Bob은 Alice의 public key를 보고 Key를 위와 같은 방식으로 만듭니다.

Saber.KEM.Decaps($sk = (z, pkh, pk, \bm{s})$)

1.ㅤ$m’ = \text{Saber.PKE.Dec}(\bm{s}, c)$

2.ㅤ$(\hat{K}’, r’) = \mathcal{G}(pkh, m’)$

3.ㅤ$c’ = \text{Saber.PKE.Enc}(pk, m’; r’)$

4.ㅤ$\text{if} \ c = c’ \ \text{ return } K = \mathcal{H}(\hat{K}’, c)$

5.ㅤ$\text{else return } K = \mathcal{H}(z, c)$

Bob은 Alice에게 cipertext $c$를 보내주고 Alice는 이를 통해 Key를 계산해낼 수 있습니다.

5. Pros & Cons

SABER에서 모든 정수의 modulo 연산은 2의 거듭제곱이기 때문에 단순한 비트 연산으로 처리 가능합니다. 또한 Ring을 정해두었기 때문에 확장이 필요할 때 rank만 늘리면 됩니다.

Pseudorandom이 덜 쓰이고 전체의 연산 과정에서 곱셈을 보면 늘 $\beta_\mu(R_q)$으로 구해진 작은 다항식만을 곱합니다. 그렇기 때문에 multiplication을 간단한 shift와 addition으로 대체할 수 있습니다.

반면 ring의 특성상 다항식 연산에서 속도를 올릴 수 있는 NTT를 적용할 수 없고 Signature scheme이 지원되지 않습니다.

6. Conclusion

이번 글에서는 SABER를 다루어보았습니다. Round 3이 끝나고 어떤 암호가 선정될지는 알 수 없지만 Lattice에서 심각한 결함이 발견되지 않는 한 Lattice-based Cryptosystem이 선정될 것 같다는 근거없는 저의 뇌피셜이 있습니다. 그렇기 때문에 LWE, LWR등에 대해 얕게나마 이해를 하고 있으면 분명 언젠가 써먹을 순간이 있다고 생각합니다.

Lattice-based cryptography를 공부하면서 자료가 부족해 정말 애를 먹었는데 그 기억을 바탕으로 나름대로 풀어서 친절하게 설명을 해보려고 했습니다. 하지만 PQC 자체가 많은 배경지식을 필요로 하는 내용인데 거기에 더 나아가 실제로 제안된 암호 시스템을 소개하려다 보니 이 글도 처음 보는 사람에게 그다지 친절한 글이 아닌 것 같아 조금 아쉽습니다. 그래도 재밌게 읽어주셔서 감사합니다.