Error-bounded Piecewise Linear Representation
안녕하세요?
오늘은 주어진 데이터를 여러 개의 선형 방정식으로 근사하되, 모든 점들마다 최대 오차가 $\delta$ 이하로 bound되도록 하는 Error-bounded Piecewise Linear Representation를 구하는 방법에 대해 알아보겠습니다.
이 글의 내용은 2014년 발표된 논문인 Maximum error-bounded Piecewise Linear Representation for online stream approximation을 참고하였습니다.
PLR이란?
Piecewise Linear Representation(PLR)은 주어진 데이터를 구간마다 여러 개의 선형 방정식으로 근사하는 방법입니다.
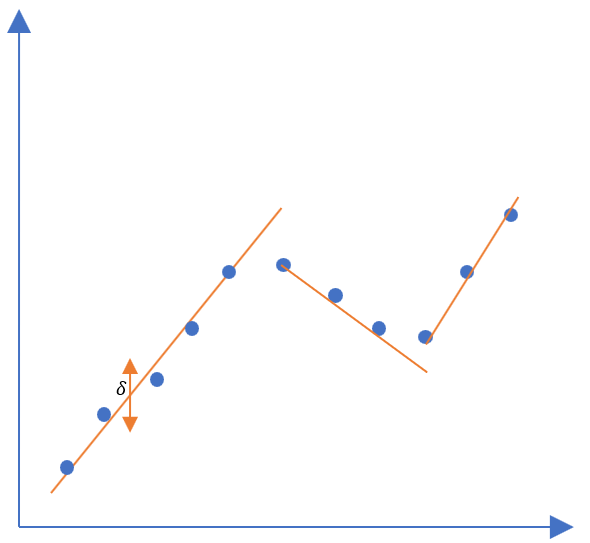
PLR을 사용하면 얻을 수 있는 이점은 데이터의 절약입니다. 위 Fig 1는 총 11개의 데이터를 포함하고 있지만, 해당 데이터를 3개의 선으로 근사한다면 하나의 선마다 ($y = ax + b$에서의 상수 $a$와 $b$, 시작점의 위치 $x_i$)만을 저장하면 되기 때문에 총 9개의 데이터만을 저장하면 됩니다.
이렇듯, PLR은 경향성이 존재하는 데이터에 대해서는 저장해야 하는 정보의 양을 크게 줄이는 효과를 보일 수 있습니다.
근사하는 방법은 여러 종류가 있을 수 있지만, 오늘 알아볼 것은 그 중 maximum error가 $\delta$ 이하가 되도록 하면서, 선의 개수가 가장 적게 나오도록 하는 근사법입니다. 각 구간을 표현하는 선들이 서로 연속적일 필요는 없습니다.
OptimalPLR
선의 개수가 가장 적게 나오도록 하는 방법이 잘 떠오르지 않는다면, line으로 representation하지 않고 측정 상수로 representation하는 방법인 PCR(Piecewise Constant Representation)을 먼저 떠올려보겠습니다.
이 경우, 문제의 난이도가 훨씬 더 쉬워집니다. 데이터를 순서대로 쭉 보면서, 해당 구간의 maximum과 minimum의 차이가 $2 \delta$보다 작을 때까지는 항상 해당 데이터들을 error가 $\delta$ 이하인 하나의 상수로 표현할 수 있습니다.
차이가 $2 \delta$보다 커진 경우 어떠한 방법으로도 해당 구간을 error가 $\delta$ 이하가 되도록 상수로 표현할 수 없으니, 이 때부터 새로운 구간을 다시 시작하면 됩니다. 이렇게 greedy한 방법으로 optimal한 PCR을 찾아낼 수 있습니다.
수식으로 작성해보면, 구간 i~j에 대해 $\max_{i \le i_1 < i_2 \le j}{|y_{i_1} - y_{i_2}|} <= 2\delta$를 만족할 경우 해당 구간 i~j를 하나의 constant로 나타낼 수 있습니다.
PLR을 찾는 과정도 고려할 것은 훨씬 더 많지만, 방법 자체는 이와 크게 다르지 않습니다. 데이터를 순서대로 보며 해당 구간이 하나의 line으로 표현될 수 있는지를 확인하고, 더이상 하나의 line으로 표현될 수 없을 때 새로운 구간을 시작해주면 됩니다.
가장 먼저, PLR을 PCR 문제처럼 바꾸어봅시다. x축과 $\theta$의 각도를 이루는 선에 대한 가능성을 알아보기 위해, 좌표축을 $-\theta$만큼 회전시켜주면 PCR 문제로 바꿀 수있습니다. 이 경우 좌표는 다음과 같이 변환됩니다.
$p = x \cos{\theta} + y \sin{\theta}$, $q = -x \sin{\theta} + y \cos{\theta}$
이 경우, 앞에서와 같이 $\max_{i \le i_1 < i_2 \le j}{| q_{i_1} - q_{i_2} |} <= 2\delta|\cos{\theta}|$를 만족할 경우 구간 i~j를 하나의 line으로 만들 수 있습니다.
좌표를 변환하는 식을 대입한 후 식을 간단히 정리하면, 최종적으로 $\frac{(y_j - \delta) - (y_i + \delta)}{(x_j - x_i)} \le \tan{\theta} \le \frac{(y_j + \delta) - (y_i - \delta)}{(x_j - x_i)}$를 만족하면 됩니다.
여기서 $\tan{\theta}$는 그래프의 기울기이므로, 우리는 가능한 기울기의 상한과 하한을 알 수 있게 됩니다.
따라서, 구간 [1,k-1] 사이의 모든 pair (i, j)에 대해 위 식을 통해 상한과 하한을 구한 뒤, 하한 <= 상한을 만족할 경우 해당 구간을 하나의 line으로 나타낼 수 있습니다.
이제 이 상황에서 하나의 점 (k번)을 더 추가할 때, 이 점을 추가할 수 있는지를 판별해봅시다.
그에 앞서, 한 가지 특성을 먼저 확인하고 가야 합니다.
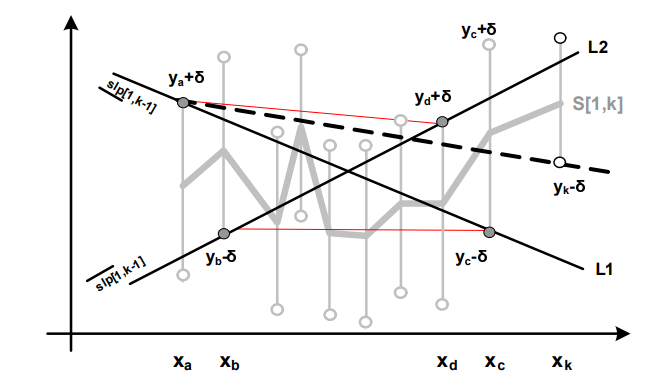
Lemma 1. a, c를 기울기의 하한이 되는 두 점, b, d를 기울기의 상한이 되는 두 점이라고 하였을 때 모든 $1 \le i \le k -1 $인 모든 $x_i$에 대해 [$y_i - \delta$, $y_i + \delta$]는 두 선 모두와 만나게 됩니다.
이를 증명하는 것은 간단한데, 만나지 않는다고 가정할 경우 더 낮은 하한/상한이 되는 선을 찾을 수 있기 때문입니다.
따라서 이 두 선을 기준으로, $y_i + \delta$는 항상 선의 위쪽에, $y_i - \delta$는 항상 선의 아래쪽에 놓이게 됩니다.
이제 새로운 점 k가 추가되었을 때, 이 k의 범위에 대한 힌트를 얻을 수 있는데, 바로 [$y_k - \delta$, $y_k + \delta$]는 하한을 나타내는 선 아래에 있거나 상한을 나타내는 선 위에 있으면 안된다는 것입니다.
만약 상한을 나타내는 선 위쪽에 있다고 가정해봅시다. 바로 위에서 확인한 Lemma 1에 의해, [$y_i - \delta$, $y_i + \delta$]는 1~k번 점을 bounding하는 선과 만나야 하는데(현재 우리는 이 선이 무엇인지는 정확히 모릅니다), 이 선은 또한 1~k-1번 점을 bounding하는 선에 의해 bounding됩니다. 따라서 절대로 위의 Lemma 1을 만족할 수 없습니다.
이렇게 k번 점의 line에 포함될 수 있는 y축 범위를 구했으며, 해당 범위에 점이 들어온다면 1~k번 점까지 하나의 line으로 표현 가능하게 됩니다.
이제 해주어야 할 일은 k번 점까지 포함하는 새로운 상한과 하한을 구하는 것입니다.
원래라면 1~k번 점들 사이의 모든 pair (i, j)에 대해 확인을 진행해주어야 하지만, 우리는 1~k-1번 점에 대한 상한과 하한을 알고 있습니다. 따라서 1, 2, …, k - 1번 점과 k번 점들 사이만을 비교해보아도 충분합니다. 하지만 이 또한 점 하나를 update하는 데에 많은 시간이 소요되게 됩니다. 이를 조금 더 줄여볼 수 있을까요?
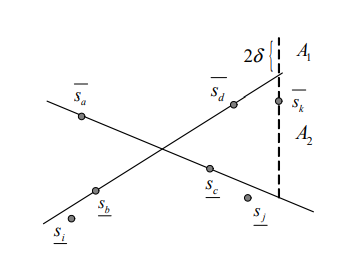
$y_k + \delta$의 범위는 Fig 3에 표시된 것과 같으며, 이 중 상한을 나타내는 선의 위쪽을 A1, 아래쪽을 A2라고 해 봅시다. b번 점 앞쪽에 있는 점 i에 대해서는, 만약 $y_k + \delta$가 A1에 있다면 기존 상한(1~k-1번)의 기울기보다 크고, A2에 있다면 점 $y_b - \delta$가 항상 선 위에 있게 되므로 Lemma 1에 어긋납니다.
마찬가지로, c번 점 뒤족에 있는 점에 대해서도 $y_b - \delta$가 항상 선 위쪽에 위치하게 되므로 Lemma 1에 모순이 발생합니다. 따라서, b번 점 앞쪽에 있는 점과 c번 점 뒤쪽에 있는 점은 확인하지 않아도 충분합니다.
하한에 대해서도 같은 논리를 적용할 수 있으며, 따라서 하한의 경우 a~d번 사이의 점, 상한의 경우 b~c번 사이의 점만 확인해도 충분합니다.
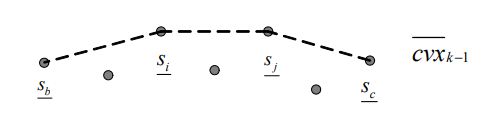
마지막으로, b~c번 점을 확인할 때 해당 점들의 convex hull만을 확인하면 된다는 사실 또한 알 수 있습니다. Fig 4를 참고하여, convex hull 내부에 있는 점에 대해서는 해당 점과 k번 점의 상한을 이어주는 선이 convex hull의 line과 만나게 되므로, 최소한 이어주는 선의 위쪽에 위치한 점이 하나는 위치하게 되며, 이는 Lemma 1에 모순이 일어나기 때문입니다. 따라서 convex hull을 잘 유지해 줄 경우, 확인해야 하는 점의 수를 극단적으로 크게 줄이는 것이 가능합니다.
이외에도 두 가지의 추가적인 최적화를 적용하여, 최종적으로 시간 복잡도 $O(n)$에 완전한 OptimalPLR을 구할 수 있습니다.
Reference
다음은 이번 글을 작성하는 데에 참고한 자료들입니다. 설명의 편의를 위해 여러 수학적 표현들을 삭제하였으니, 관심있는 사람들은 원본 논문을 참고해주시기 바랍니다.
Maximum error-bounded Piecewise Linear Representation for online stream approximation