A Generalized Birthday Problem
안녕하세요, 이번 글에서는 CRYPTO 2002에 소개된 David Wagner - A Generalized Birthday Problem 논문의 내용을 따라가며 논문에서 소개하는 Birthday Problem의 확장을 알아보겠습니다.
Introduction
Classic Birthday Problem
Birthday Problem은 직관과 다르게 23명 이상만 있어도 그 중 두 명의 생일이 같을 확률이 1/2를 넘는다는 내용의 문제이고 별도의 설명이 필요한가 싶을 정도로 너무나 유명한 내용입니다.
암호학에서는 대표적으로 해쉬 함수가 N-bit이라고 할 때 해쉬값이 같은 두 입력을 찾기 위해서 $O(2^{N/2})$개의 입력에 대한 차분을 보면 된다는 정리가 Birthday Problem으로부터 도출되고 PS 분야에서는 Meet In The Middle 알고리즘이 Birthday Problem과 관련 있습니다.
논문에서는 ${0, 1}^n$ 꼴의 $L_{1}, L_{2}$ 원소들 중에서 $x_1 \oplus x_2 = 0$을 만족하는 $x_1 (\in L_1), x_2 (\in L_2)$를 구하는 문제로 설명을 하고 있습니다.
일단 $|L_1| \times |L_2| » 2^n$일 때 이러한 $x_1, x_2$가 존재할 것으로 기대할 수 있고 list의 크기를 임의로 정할 수 있을 때 $\Theta(2^{n/2})$에 $x_1, x_2$를 구할 수 있음은 매우 자명해보입니다.
그런데 list의 개수를 2개에서 $k$개로 늘린다면 어떻게 될까요?
Generalized Birthday Problem
list의 개수가 2개가 아니고 $k$개이면 ${0, 1}^n$ 꼴의 $L_1, L_2, \dots, L_k$ 원소들 중에서 $x_1 \oplus x_2 \oplus \dots \oplus x_k = 0$을 만족하는 $x_i (\in L_i)$를 구하는 문제가 됨을 알 수 있습니다.
이 때 논문에서는 리스트의 크기는 임의로 정할 수 있고 원소는 uniformly random하게 뽑힌 상황을 가정합니다. 주어진 원소들에서 $x_i (\in L_i)$를 찾는 상황과 원소가 uniformly random하게 뽑히는 상황에는 분명한 차이가 있음에 유의해야 합니다.
예를 들어 리스트가 4개일 때 모든 원소가 uniformly random하게 뽑히면 각 리스트의 크기가 대략 $2^{n/4}$ 정도이면 높은 확률로 해가 있다고 생각할 수 있습니다. 그러나 원소가 주어지면 리스트가 ${0,0,0,\dots , 0}, {0,0,0,\dots , 0}, {0,0,0,\dots , 0}, {1,1,1,\dots , 1}$와 같을 때 각 리스트의 크기가 아무리 크더라도 해는 절대 존재할 수 없습니다.
일단 $|L_1| \times |L_2| \times \dots |L_k| » 2^n$이면 해가 존재하긴 할텐데 어떻게 효과적으로 구할 수 있을까요?
누군가 한 번쯤은 생각해봤을 내용인 것 같은데 신기하게도 이 논문 이전에는 관련 연구가 없었다고 합니다. 이 논문에서는 Generalized Birthday Problem의 효율적인 공격법과 이 공격법을 이용한 실제 암호 시스템에 대한 분석이 진행될 예정입니다.
Algorithms
Classic Birthday Problem
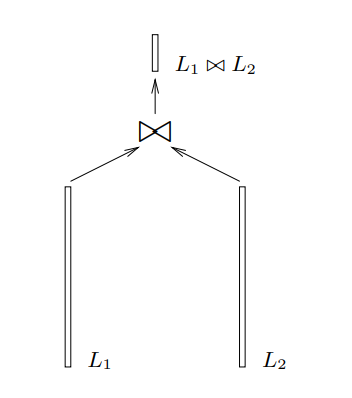
Classic Birthday Problem은 단순히 $L_1 \Join L_2$을 구하면 됩니다. Join을 구하기 위해 hash table을 이용하면 $O(|L_1|+|L_2|)$, merge-join을 이용하면 $O(nlgn), n = max(|L_1|, |L_2|)$에 해결 가능합니다.
4-list Birthday Problem
리스트가 2개에서 4개로 늘어났습니다. $L_1, L_2, L_3, L_4$에서 $x_1 \oplus x_2 \oplus x_3 \oplus x_4 = 0$을 찾고 싶습니다.
리스트가 4개가 되었다고 하더라도 $O(2^{n/2})$ 풀이는 자명하게 사용할 수 있습니다. 그러나 이 논문 이전에는 더 효율적인 방법이 없었다고 합니다.
참고로 4-list Birthday Problem을 4-Sum problem이라고도 부릅니다.
어떻게 하면 문제를 해결할 수 있을까요?
사실 방법을 알고 나면 그렇게 어려운 내용은 아닙니다. 만약 이 문제가 코드포스 인터랙티브 문제로 나왔다면 분명 누군가는 풀어냈을 것 같습니다. 그렇기 때문에 바로 알고리즘을 확인하기 보다는 $O(2^{n/2})$ 보다 개선할 방법에 대해 고민하는 시간을 조금만 가지고 진행하면 좋을 것 같습니다.
알고리즘을 설명해보겠습니다.
4-list Birthday Problem은 마치 월드컵 토너먼트와 같이 리스트 2개를 먼저 합친 리스트를 만들고 합쳐진 리스트 2개를 다시 합치는 방식을 사용하면 효율적으로 구현할 수 있습니다.
먼저 용어를 정리해보면 $\Join_l =$ LSB-$l$ bit에 대한 join을 의미합니다. 00111과 01111은 join하면 공집합이 되지만
$\Join_3$의 경우 LSB-3 bit이 111로 동일하기 때문에 join을 할 수 있습니다.
알고리즘의 과정은 아래와 같습니다.
-
4개의 리스트 $|L_1|, |L_2|, |L_3|, |L_4|$의 크기를 $n/3$으로 둡니다. 그 후 $L_{12} = L_1 \Join_{n/3} L_2, L_{34} = L_3 \Join_{n/3} L_4$ 로 정의합니다. 이 때 $E[|L_{12}|] = |L_1| \cdot |L_2| / 2^{n/3} = 2^{n/3}$, 마찬가지로 $E[|L_{12}|] = 2^{n/3}$가 됩니다.
-
1로부터 계산된 $L_{12}, L_{34}$의 각 pair에서 LSB-$n/3$ bit는 일치하므로 $E[|L_{12} \Join L_{34}|] = |L_{12}| \cdot |L_{34}| / 2^{n-n/3} = 1$으로 해를 구하는데 성공했습니다.
-
1, 2번 과정 모두 $O(2^{n/3})$의 시간/공간 복잡도에 구현 할 수 있으므로 4-list Birthday Problem은 $O(2^{n/3})$에 해결 가능합니다.
즉 $\Join_{n/3}$을 통해 문제를 해결할 수 있었습니다. 이 과정을 그림으로 나타내면 아래와 같습니다.
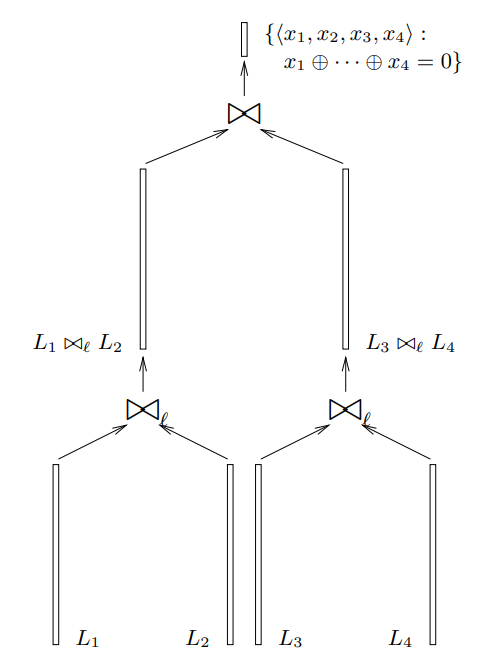
8, 16, 32, $\cdots$-list Birthday Problem 또한 둘씩 짝지어 올라가는 방식을 이용하면 됩니다. 리스트가 4개일 땐 $\Join_{n/3}$을 사용했는데 리스트가 8개일 땐 $\Join_{n/4}$를 사용해야 하고 리스트가 16개일 땐 $\Join_{n/5}$를 사용해야 합니다. 최종적으로 $k$-list Birthday Problem을 $O(k \cdot 2^{n/(1+lgk)})$에 해결할 수 있습니다.
그 다음으로 4-list Birthday Problem의 여러 확장을 생각해보겠습니다. 지금은 $x_1 \oplus x_2 \oplus x_3 \oplus x_4 = 0$인 경우만 계산을 하는데 $x_1 \oplus x_2 \oplus x_3 \oplus x_4 = \alpha$인 경우는 $L_4$의 각 원소에 $\alpha$를 XOR한 후 위의 알고리즘을 적용하면 되므로 상황이 동일합니다.
또한 XOR 대신 $(\mathbb{Z}/2^n\mathbb{Z}, +)$에서 $x_1 + x_2 + x_3 + x_4 = 0$을 찾는 문제도 약간의 변형으로 계산 가능합니다. 크게 어렵지는 않기 때문에 이 부분에 대한 설명은 생략하겠습니다.
지금은 한 개의 해만을 찾는데 주력했는데 여러 개의 해를 찾고 싶으면 어떻게 하면 될까요? 가장 직관적인 방법은 동일한 방법을 여러 번 돌리는 것입니다. 이렇게 하면 $\alpha$배의 연산으로 $\alpha$개의 해를 구할 수 있습니다.
그런데 이 대신 각 리스트의 크기를 $\alpha \cdot 2^{n/3}$개로 두면 기대값을 계산했을 때 $\alpha^3$개의 해를 구할 수 있습니다. 즉 $\alpha$배만큼 더 연산해서 $\alpha^3$개의 해를 구할 수 있게 됩니다. 단 $\alpha \leq 2^{n/6}$를 만족해야 합니다.
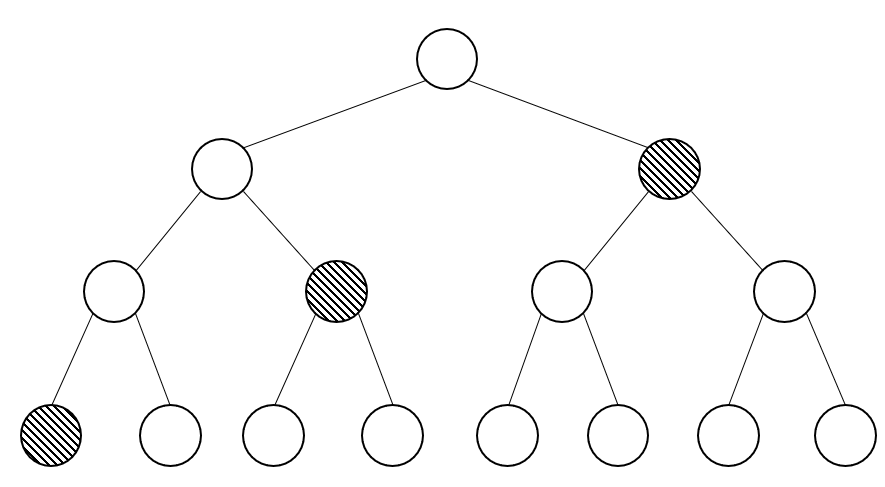
그리고 $k$-list Birthday Problem을 해결할 때 계산의 중간 과정에서 최대 $k$개의 리스트가 추가로 생성됩니다. 이들을 끝까지 저장하는 대신 postfix order로 처리하며 더 이상 필요 없는 리스트는 저장하지 않으면 $lg k$개만 저장해도 됩니다.
Lower bounds
앞에서 소개한 방법을 통해 $k$-list Birthday Problem을 $O(k \cdot 2^{n/(1+lg k)})$에 해결할 수 있게 되었습니다. 그런데 이 문제의 Lower bound는 어떻게 될까요?
일단 한가지 확실한건 $max(|L_i|) \geq 2^{n/k}$일 때 해의 개수의 기대값이 1 이상이니 $\Omega(2^{n/k})$입니다. 이 값과 실제 우리가 알아낸 $O(k \cdot 2^{n/(1+lg k)})$의 차이는 아직 많이 큽니다. 이 lower bound를 개선해볼 방법을 고민해봅시다.
Relation to discrete logs
Lower bound를 개선하기 위해 discrete log problem을 가져오려고 합니다.
만약 Cyclic group $G = \langle g \rangle$에서의 $k$-list Birthday Problem을 $t$의 시간에 해결할 수 있으면 DLP 또한 $O(t)$에 해결 가능합니다. 왜냐하면 $g^0, g^1, g^2, \dots$등에 대해 $k$-list Birthday Problem을 해결하도록 하면 되기 때문입니다.
그리고 $G$의 특별한 성질을 사용하지 않는 일반적인 DLP의 알고리즘이 $\Omega(\sqrt{p})$이므로 $k$-list Birthday Problem 또한 $\Omega(\sqrt{p})$임을 알 수 있습니다.
또한 Order가 $m$인 group $G = \langle g \rangle$에서의 $k$-list Birthday Problem을 $t$의 시간에 해결할 수 있고 리스트의 크기가 $l$인 $(\mathbb{Z}/m \mathbb{Z}, +)$에서의 $k$-list Birthday Problem을 $t’$의 시간에 해결할 수 있다면 $k$-list Birthday Problem over G with list of size $l$을 $t’ + klt$의 시간에 해결할 수 있습니다. 갑자기 기호가 쏟아져서 조금 당황했을수도 있는데 $L’_i = {log_gx : x \in L_i}$로 정의했을 때 $L’_i$에 대한 $k$-list Birthday Problem을 해결하면 자연스럽게 저 식이 나옴을 알 수 있습니다.
Attacks and applications
지금까지 Generalized Birthday Problem을 다방면으로 알아보았는데 이것들은 어디에서 활용될 수 있을까요? 논문에서 제시된 몇 가지 응용 사례를 살펴보겠습니다.
Blind signatures
Digital Signature는 sender가 자신의 신원을 증명하는 방법으로, 인증/무결성/부인 방지 기능을 제공합니다. 그리고 Blind signature는 signer가 내용을 모른채 sign을 할 수 있는 암호 시스템입니다. 모네로, 대시와 같은 다크코인이 Blind signature을 사용합니다.
Blind signature는 공개키 암호 시스템의 과정과 비슷한 방식으로 구현될 수 있고 그 중에서 Schnorr blind signature라는 이름의 방식이 있습니다. Schnorr blind signature는 discrete log problem이 어려운 그룹에서의 연산을 이용한 방식입니다. 자세한 설명은 링크를 참고해주세요.
Schnorr blind signature는 DLP가 쉽게 풀릴 시 쉽게 타인이 서명을 위조할 수 있게 됩니다. 뿐만 아니라 $k$-list Birthday Problem을 풀어낼 수 있다면 $k-1$번의 서명 요청으로 $k$개의 서명을 얻을 수 있습니다.
만약 그룹의 order가 $2^{160}$이라고 한다면 이전에는 $k$-list Birthday Problem을 $2^{80}$에 풀어냈으므로 크게 실현 가능한 공격이 아니었지만 지금은 $O(k \cdot 2^{n/(1+lg k)})$에 공격을 수행할 수 있으므로 $k = 2^9$ 정도일 때 $O(2^{25})$의 시간에 공격이 가능하게 됩니다.
NASD incremental hash
사실 저도 이 논문을 읽으면서 NASD라는 것을 처음 알게 되었습니다. 설명을 보니 클라우드 내지는 구글 드라이브와 비슷한 시스템인 것 같은데, NASD가 무엇인지를 정확하게 알 필요는 없습니다.
NASD에서는 integrity check를 위해 $H(x) = \Sigma_{i=1}^k h(i, x_i) \space mod \space 2^{256}$라는 형태의 해시 함수를 사용합니다. 당연히 $H$에서의 collision을 찾을 수 있다면 integrity check가 믿을 수 없게 될 것이고 이 문제는 $(\mathbb{Z}/2^{256} \mathbb{Z}, +)$에서의 Birthday Problem 문제로 변환해서 생각할 수 있습니다.
이외에도 AdHash, PCIHF hash 등이 비슷한 문제를 가지고 있습니다. 개인적으로 생각할 때 해시 함수가 $(\mathbb{Z}/m \mathbb{Z}, +)$ 꼴의 ring에서 정의된 연산을 이용하는 것은 그렇게 바람직하지 않은 것 같습니다.
Low-weight parity checks
이 공격은 stream cipher와 관련이 있는 공격입니다. $p(x)$가 irreducible polynomial of degree n over GF(2) 라고 할 때, weight가 굉장히 작으면서 degree는 그렇게 크지 않은 $p(x)$의 배수 $m(x)$를 찾고자 합니다.
이런 $m(x))$를 찾을 수 있다면 fast crrelation attack을 통해 stream cipher의 결과로부터 seed를 유추해낼 수 있게 됩니다. $m(x)$를 찾기 위해 $GF(2)[t]/p(t)$에서 $t^0, t^1, t^2, \dots$들을 가지고 $k$-list Birthday Problem을 계산하면 됩니다.
Open problems
Other values of $k$
논문에서 제시한 방법은 $k$가 $2^a$ 꼴일 때 사용할 수 있는 방법입니다. $k$가 $2^a$ 꼴이 아닐 때에는 더 효율적인 방법이 없을까요?
예를 들어 $k = 3$일 때 $x_1 \oplus x_2 \oplus x_3 = 0$을 만족하는 해를 찾는 방법이 $O(2^{n/2})$보다 효율적일 수는 없을까요?
Other combining operations
논문에서 다룬 $\oplus, +$ 이외의 다른 연산들에서 더 효율적인 방법이 있을까요?
Golden solutions
주어진 $x_1 \oplus x_2 \oplus \dots \oplus x_k = 0$의 해는 여러 개일 수 있습니다. 이중에서 Golden solution이라고 이름 붙은 단 1개의 해가 우리에게 의미있는 해라면 Golden solution을 빠르게 찾아낼 수 있는 방법이 있을까요? 그리고 지금은 $x_1 \oplus x_2 \oplus \dots \oplus x_k = 0$의 해 중에서 어느 1개만을 찾는데 모든 해를 다 찾아야 하는 상황일 때에는 어떻게 할 수 있을까요?
Memory and communication complexity
보통 $N$ bytes의 메모리가 $N$번의 연산보다 비용이 비쌉니다. 그래서 memory-time tradeoff나 아예 memory를 획기적으로 줄일 방법이 있다면 도움이 될 것입니다. Classic birthday problem은 Pollard’s rho와 같은 방법으로 메모리를 획기적으로 줄인 적이 있기 때문에 Generalized birthday problem에서도 방법이 있을 수 있습니다.
Lower bounds
비록 DLP와의 관계를 이용해 간접적으로 Lower bound를 유추하긴 했지만 아직 provable lower bound는 $k$-list Birthday Problem 기준 $\Omega(2^{n/k})$로 많이 부족합니다.
Conclusions
이 논문을 통해 $k$-list Birthday Problem을 해결하는 효율적인 알고리즘과 그 응용 방안들을 다루었습니다.
개인적으로는 3-list Birthday Problem을 $O(2^{n/2})$보다 효율적으로 푸는 방법이 아직 없다는 점이 조금 의외였고 마치 PST와 같은 형태로 Trie를 만들어서 해결이 가능하지 않을까 싶어 고민을 해보았지만 쉽지 않았습니다.
이 글을 통해 Generalized Birthday Problem을 이해하는데 도움이 됐으면 좋겠습니다.