Huffman coding과 Data entropy
안녕하세요?
오늘은 압축 알고리즘에 대한 설명을 진행해보려 합니다.
Lossless Data Compression
데이터 압축은 굉장히 중요한 기술 중 하나입니다.
데이터 압축의 가장 큰 장점은 뭐니뭐니해도, 사용하는 공간의 크기를 줄일 수 있다는 점입니다. 저장장치의 크기는 정해져 있는데, 이 곳에 데이터를 압축하여 저장한다면 같은 비용으로 더 많은 데이터를 저장할 수 있게 됩니다.
데이터 압축의 또 다른 장점으로는, Bandwidth를 높여주는 효과를 가져온다는 점입니다. 예를 들어서 통신을 할 때, 통신 속도가 충분히 빠르지 않다면 이 과정이 병목이 될 가능성이 높습니다.
이 때 데이터를 압축하고 보내고, 다시 압축해제 한다면 이러한 병목을 완화할 수 있습니다.
이러한 데이터 압축은 크게 lossless data compression과, lossy data compression으로 나눌 수 있습니다. 이름에서 알 수 있듯이 전자는 압축한 데이터를 다시 원본과 똑같이 복원해낼 수 있고, 후자는 데이터 손실이 발생합니다.
Lossy data compression은 이미지와 같은, 어느 정도 손실이 발생하여도 크게 지장을 미치지 않는 곳에 보통 사용됩니다. jpg 파일이 대표적인 lossy data compression입니다. 하지만, 대부분의 데이터는 손실이 일어나면 곤란한 경우가 많으므로 더 일반적으로 사용가능한 것은 lossless data compression입니다.
이번 글에서는 lossless data compression 중, data entropy를 기반으로 작동하는 압축 알고리즘들을 살펴보도록 하겠습니다. Data entropy를 기반으로 작동한다는 것은, 압축률이 데이터 내에서 각 소단위(예를 들어 byte)들이 출현하는 빈도와 관련된다는 것입니다.
Huffman Coding
Huffman coding은 가장 대표적이고, 간단하지만 좋은 성능을 가지는 데이터 압축 기법입니다.
Huffman coding의 아이디어는 출현 빈도가 높은 데이터를 짧은 binary code로 나타내서, 최종적으로 bit 수를 줄이겠다는 아이디어입니다.
예를 들어서, 아래와 같은 데이터를 압축하는 상황을 가정해보도록 하겠습니다. 아래의 모든 예시에서, 빈도의 측정은 byte 단위로 진행된다고 가정하겠습니다.
string = “AAABBCDDDDAAAADD”;
각 문자별로 빈도수를 세어보면, 아래와 같습니다.
| 문자 | 빈도 | 비율 |
|---|---|---|
| A | 7 | 0.4375 |
| B | 2 | 0.125 |
| C | 1 | 0.0625 |
| D | 6 | 0.375 |
출현 빈도수가 높은 A, D에 더 짧은 binary code를 할당하는 것이 합리적입니다. 반면, B와 C는 출현 횟수가 많지 않으므로 긴 binary code를 할당하여도 큰 부담이 없습니다. 이제 binary code를 할당하는 법을 살펴보겠습니다.
각 문자별로 binary code를 할당하는 것은, heap을 이용한 greedy algorithm을 사용하여 가능합니다.
이 때, 모든 binary code들은 “한 binary code가 다른 binary code의 접두사가 되지 않아야 한다“는 조건을 만족해야 합니다. 하나가 다른 하나의 접두사가 되면, decode를 진행할 때 동일한 접두사를 가진 둘을 구분할 수 없게 되기 때문입니다.
이 때 만약 모든 binary code를 이진 트리로 나타내보면 어떻게 될까요? head부터 시작하여, 왼쪽 child로 이동하는 것을 0, 오른쪽 child로 이동하는 것을 1로 나타내봅시다. 트리를 따라 내려가 leaf에 도착하면 현재까지 경로가 나타내는 binary code가 해당 leaf가 가진 문자를 나타내게 됩니다.
만약 한 code가 다른 code의 접두사가 된다면, 접두사가 되는 code의 child를 따라 내려가면 다른 code를 발견할 수 있게 됩니다. 모든 leaf는 다 하나의 문자를 나타내고 있으므로, 결국 위 조건을 만족하려면 모든 code는 leaf에서 끝나야 합니다.
마지막으로, child를 하나 가지고 있는 node가 있을 경우 해당 노드를 제거하는 것이 더 짧은 binary code를 만들어낼 수 있으므로, 만들어진 tree는 항상 완전 이진 트리가 된다고 가정할 수 있습니다.
이를 만족하는 트리의 예시는 아래 그림 1과 같습니다. 이를 Huffman tree라고 합니다.
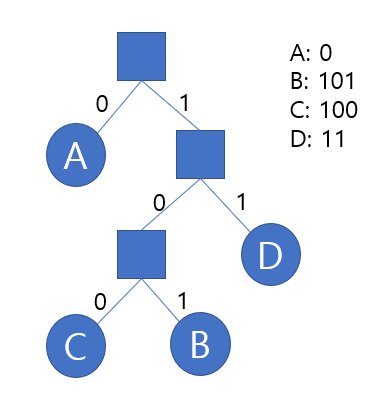
그림 1. Huffman tree의 예시
각 문자의 binary code의 길이는, 해당 문자가 위치한 node의 depth와 간다는 사실도 금방 유추해낼 수 있습니다. 그럼 이러한 tree 중, 전체 길이가 최소가 되는 tree는 어떻게 만들 수 있을까요?
이를 만드는 방법은 매우 간단한데, 바로 출현 빈도가 가장 작은 두 문자열부터 차례로 합쳐주는 방법입니다. 한 번 합칠 때, 합쳐지는 노드의 subtree에 위치하는 문자의 출현 빈도의 합만큼 전체 길이가 길어지기 때문에, 가장 작은 두 node부터 합쳐주는 greedy한 방법이 쉽게 성립할 수 있습니다.
아래 그림 2는 Huffman tree를 만드는 과정을 나타낸 그림입니다.
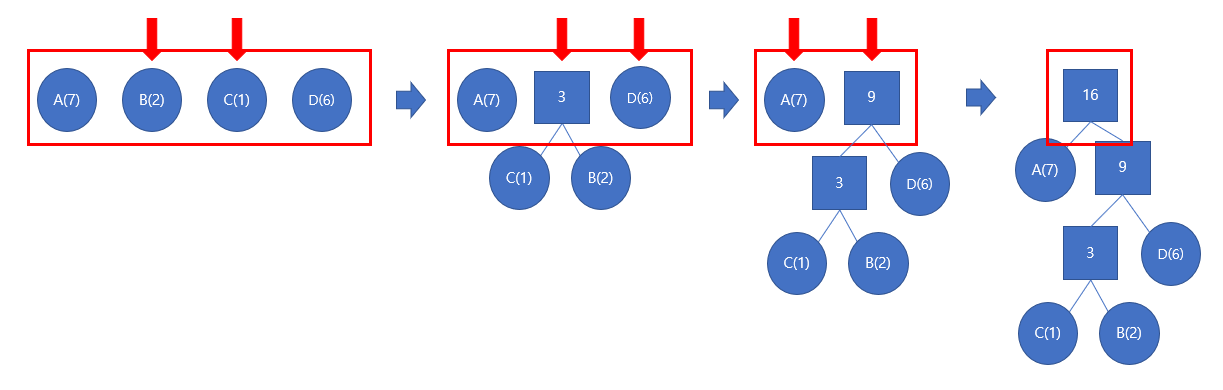
실제 Huffman tree를 만드는 과정은, 최소 힙을 사용하여 쉽게 가능합니다. 아래는 Huffman tree를 만드는 code입니다.
struct Node {
bool leaf;
char c;
Node* left = nullptr;
Node* right = nullptr;
};
Node* build_huffman(char* str, int len) {
int cnt[256] = {};
for (int i = 0; i < len; ++i) {
cnt[str[i]]++;
}
priority_queue<in, vector<in>, greater<in>> pq;
for (int i = 0; i < 256; ++i) {
Node* node = new Node;
node->leaf = 1;
node->c = i;
if (cnt[i]) pq.push({cnt[i], node});
}
while (pq.size() != 1) {
Node* node = new Node;
int cnt = 0;
node->leaf = 0;
cnt += pq.top().first;
node->left = pq.top().second;
pq.pop();
cnt += pq.top().first;
node->right = pq.top().second;
pq.pop();
pq.push({cnt, node});
}
return pq.top().second;
}
Huffman tree가 만들어졌으면, encoding과 decoding은 해당 tree를 이용하여 쉽게 진행할 수 있습니다. 단, encode의 경우 문자에서 tree를 거슬러 올라가는 것은 비효율적이기 때문에 tree를 순회하며 미리 binary code를 모두 저장해놓는 것이 구현을 하는 데에 효율적입니다.
코드는 아래와 같습니다. 아래 구현에서는 편의성을 위해 0과 1로 구성된 문자열을 생성하는데, 이 경우 한 bit당 1바이트씩 차지하므로 실제로는 각각의 bit로 저장해야 합니다. 문자열을 생성하는 것은 bit를 생성하도록 바꾸는 것은 크게 어렵지 않으므로, 해당 구현은 생략하겠습니다.
int sz;
char* code[256];
char code_now[256];
void make_code(Node* node) {
if (node->leaf) {
code[node->c] = new char[sz];
for (int i = 0; i < sz; ++i) code[node->c][i] = code_now[i];
return;
}
code_now[sz++] = '0';
make_code(node->left);
sz--;
code_now[sz++] = '1';
make_code(node->right);
sz--;
}
int encode(char* ori, char* des, int len, Node* head) {
make_code(head);
int index = 0;
for (int i = 0; i < len; ++i) {
for (int j = 0; code[ori[i]][j]; ++j) {
des[index++] = code[ori[i]][j];
}
}
return index;
}
int decode(char* ori, char* des, int len, Node* head) {
int index = 0;
for (int i = 0; i < len; ) {
Node* node = head;
while (!node->leaf) {
if (ori[i++] == '0') node = node->left;
else node = node->right;
}
des[index++] = node->c;
}
return index;
}
bit 단위로 저장할 때 발생하는 문제점 중 하나로, padding된 문자열이 실제 encode된 것인지, 단순 padding인지 구분할 수 없다는 점이 있습니다.
예를 들어, 최종적으로 길이 9의 binary code가 생성되었다면 이를 byte단위로 저장할 경우 뒤에 7bit만큼의 공간이 남는데, decode를 진행할 때 이 부분이 실제 encode된 것인지, 단순 padding인지 구분할 수 없습니다.
이를 해결하기 위해서는 추가적으로 전체 bit의 길이를 저장하거나, EOF문자를 포함시켜 Huffman tree를 만드는 방법을 사용할 수 있습니다.
Huffman tree의 저장
데이터를 decode하기 위해서 Huffman tree가 필요하므로, huffman tree 또한 압축을 할 때 함께 저장을 해야 합니다. Huffman tree는 어떻게 저장을 해야 효율적일까요?
가장 쉬운 방법은, tree를 순회하며 leaf node가 아닐 경우 0을 적고, leaf node일 경우 1을 적고 뒤 8 bit에 leaf가 나타내는 문자를 적어주는 방법을 사용하면 간편합니다.
예를 들어, 위 그림 1에 있는 tree는 아래와 같이 저장되게 됩니다. 괄호는 구분을 위해 추가하였습니다.
01(01000001)001(01000011)1(01000010)1(01000100)
모든 문자는 리프 노드에 하나씩 놓이게 되며, tree를 만드는 과정을 생각해보면 한 번의 merge가 일어날 때 노드가 하나씩 추가되므로, Huffman tree에는 총 $2t - 1$개의 노드가 놓이게 됩니다. 여기서 t는 압축하려는 데이터에 포함된 문자의 종류입니다.
Huffman tree를 표현하는 데에 하나의 노드 당 1 bit만큼 필요하고, $t$개의 데이터를 저장하는 데 $8t$ bit이 필요하므로 추가적으로 tree를 저장하는 데에 소모되는 비용은 $10t - 1$이 됨을 확인할 수 있습니다. 일반적인 256종류의 문자를 가지는 데이터라고 가정하였을 때, 약 320byte 정도가 필요합니다.
Arithmetic coding
데이터를 압축하는 또 다른 방법으로, Arithmetic coding 방법이 있습니다.
Arithmetic coding은 개념 자체를 매우 간단하지만, 구현 난이도가 높고 계산 시간이 오래 걸린다는 단점이 있습니다.
Arithmetic coding은 전체 데이터를 0과 1 사이에 있는 단 하나의 실수로 mapping해줍니다. 이 실수가 속한 범위에 따라서, 원래 데이터를 복원해낼 수 있습니다.
간단한 예시를 확인해보겠습니다. 전체 데이터에서 출현 빈도가 아래 표와 같이 측정되었다고 가정해봅시다.
| 문자 | 비율 | 구간 |
|---|---|---|
| A | 0.6 | [0, 0.6) |
| B | 0.2 | [0.6, 0.8) |
| C | 0.1 | [0.8, 0.9) |
| [종료] | 0.1 | [0.9, 1.0) |
새롭게 구간이라는 것이 추가되었는데, 이는 각 비율의 누적합이 속하는 구간을 의미합니다.
이 때, AACB라는 문자열을 어떻게 압축할까요? 앞에서부터 구간을 줄여가는 식으로 계산하게 됩니다.
A: [0, 0.6)
AA: [0, 0.36)
AAC: [0.288, 0.324)
AACB: [0.3096, 0.3168)
AACB[종료]: [0.31608, 0.3168)
최종적으로 AACB의 구간이 확정되었습니다. 이를 이진법으로 나타내면 아래와 같습니다.
0.31608: 0.010100001110101…
0.3168: 0.0101000100011…
따라서, 이진법으로 0.01010001로 데이터를 표현할 경우, 데이터 압축을 완료할 수 있습니다.
모든 구간의 크기를 균등하게 하지 않고 비율에 따라 구간의 길이를 비례해서 정해주는 이유는, 데이터 압축이 완료되었을 때 최종 구간의 길이가 최대한 크도록 만들어주기 위함입니다. 이는 압축 효율의 향상을 가져올 수 있습니다.
또, [종료]에 해당하는 문자열을 지정해주는 것이 반드시 필요한데, 만약 [종료]에 해당하는 문자열이 존재하지 않는다면 구간을 계속 세분해서 나누어갈 수 있기 때문에 데이터의 종료를 알 수 없기 때문입니다.
Data entropy
위에서 살펴본 것과 같은 압축 기법들은 모두 “어떤 데이터가 몇 번 출현하는지“에 깊게 관련되어 있습니다.
특정 데이터가 많이 출현한다면 좋은 압축 효율을 기대할 수 있고, 반대로 다양한 데이터가 비교적 균등한 횟수로 출현한다면 압축 효율이 좋을 것이라고 기대하기 힘들게 됩니다.
이를 나타낼 수 있는 척도 중 하나가 바로 Shannon Entropy입니다. Shannon Entropy는 데이터에 포함된 정보들의 크기를 나타내는 것으로, entropy가 작으면 포함된 정보가 많지 않으므로 좋은 압축 효율을 기대할 수 있고, 반대로 entropy가 크다면 많은 정보가 포함되어 있기 때문에, 어떤 방법을 사용해도 압축된 데이터의 크기를 크게 줄이기 힘들다는 것을 의미합니다.
흔히 압축된 파일을 한 번 더 압축해보면 압축 효율이 좋지 않은 것을 확인할 수 있는데, 이는 한 번 압축을 진행하면 entropy가 굉장히 커져서, 더 이상 좋은 압축 효율을 보일 수 없기 때문입니다.
Shannon entropy는 다음과 같은 식으로 계산할 수 있습니다.
$H(X) = -\sum^{n}_{i=1} P(x_i)\log{P(x_i)}$
수식에서 각각의 항에 대해 조금 더 자세히 살펴보도록 하겠습니다.
먼저 $P(x_i)$는 각 데이터 별 출현 빈도를 나타냅니다. 여기에 로그를 붙여, $\log{P(x_i)}$를 만들면 어떤 의미를 가질까요? 이는 해당 데이터를 나타내는 데에 필요한 정보의 양을 나타내게 됩니다.
예를 들어서, 데이터가 1/4 확률로 출현한다면, 각각의 데이터들을 표현하는 데에 2 bit가 필요할 것이라고 기대할 수 있습니다. 반면 데이터가 1/8 확률로 출현한다면, 각각의 데이터들을 표현하는 데에 3 bit가 필요할 것이라고 기대해야 할 것입니다. 이런 식으로, 데이터의 출현 빈도가 낮아질수록 해당 데이터를 표현하는 데에 더 많은 양의 bit가 필요해질 것임을 알 수 있으며, 이는 확률의 로그에 비례할 것입니다.
이렇게 구한 정보의 양에 각각의 확률을 곱해 더해주게 되면, 전체 데이터에 대한 평균을 구할 수 있습니다. 다시 말해 전체 데이터를 표현하는 데에 필요한 정보의 양을 나타내게 되는 것입니다.
Entropy를 기반으로 동작하는 많은 압축 알고리즘은 결과적으로 해당 데이터가 얼마나 많은 정보를 가지고 있었는지에 따라 그 압축 효율이 결정되게 됩니다.
Reference
이상으로 entropy를 기반으로 작동하는 lossless compression 방법 두 가지를 살펴보았습니다.
글을 작성하는 데에 참고한 문서 및 사이트는 아래와 같습니다.