양자 컴퓨팅 입문 (1) - 개요
“양자(quantum)를 이용해서 상태를 저장하는 컴퓨터를 만들면 어떨까?”
이 허무맹랑할 수도 있는 1981년 리처드 파인만에 의해 제기되었습니다. 양자 컴퓨팅은 암호학 쪽에서 1997년 Shor가 다항 시간에 인수분해를 할 수 있는 양자 알고리즘을 발견하면서 각광받기 시작했습니다. 지금까지도 고전 컴퓨팅으로 인수분해를 다항 시간 안에 할 수 없고, 또 RSA 같은 많은 암호체계가 인수분해의 수학적 어려움(infeasibility)을 기반으로 두고 있는데 다항 시간에 인수분해를 할 수 있다는 소식은 획기적인 발전이었습니다. 또 Grover는 정렬되지 않은 $N$개의 항목 중 특정 조건을 만족하는 항목을 $O(\sqrt{N})$에 찾아내는 양자 알고리즘을 발견하였습니다. Simon은 hidden Abelian subgroup problem을 고전 알고리즘에 비해 지수적으로 빨리 푸는 양자 알고리즘을 발견하였습니다.
그럼 이제 RSA도 파훼되고, 세상이 양자 컴퓨터 범벅이 될 법도 한데 왜 아직도 고전 컴퓨팅 기기가 사용되고 있을까요? 물리적으로 양자 컴퓨터를 구현하는 과정이 과학적으로 대단히 힘들기 때문입니다. 최근에는 구글이 53개의 qubit을 통해 일반 슈퍼컴퓨터로 1만 년이 걸릴 계산을 200초 만에 끝냈다고 발표하며 quantum supremacy을 선언하기도 했습니다 (기사). 이런 희망찬 소식에도 불구하고 현실적으로 양자 컴퓨터가 보급되는 건 아직 멀어보일 뿐더러 양자 컴퓨터가 모든 부문에 있어 고전 컴퓨터보다 나은 것도 아니지만, 지금도 수많은 학자들과 기업들이 양자 컴퓨터 연구를 계속하고 있습니다. 암호학, 웹 검색, 유전 알고리즘 등 적용될 분야가 많기에 양자 컴퓨팅 관련된 개념을 습득해서 나쁠 건 없다고 생각합니다.
이 포스트에서는 특히, 양자 컴퓨팅의 근간이 되는 수학적 원리를 다루고자 합니다.
수학적 분석
양자 컴퓨팅을 이해하기 위해서는 어느 정도의 수학적 지식이 필요하며, 몇몇 선형대수학 표기법에 익숙해질 필요가 있습니다.
선수조건 : 선형대수학
Vector
벡터(vector), 엄밀히 말하면 열벡터(column vector)는 힐베르트 공간($\mathbb{C}^n)$의 원소인 크기 $n \times 1$의 행렬로 볼 수 있으며 다음과 같이 표기합니다.
$\mathbf{v} = \begin{bmatrix} v_1 \ v_2 \ \vdots \ v_n\end{bmatrix},\ v_i \in \mathbb{C}$
여기서 $\mathbb{C}$는 복소수의 집합을 의미합니다.
Adjoint
벡터 $\mathbf{v}$ 의 adjoint (conjugate transpose, Hermitian transpose)는 $\mathbf{v}^{\dagger}$로 표기되며, 다음과 같습니다.
$ \mathbf{v}^{\dagger} = (\mathbf{v}^T)^{} = \begin{bmatrix} v_1^{} & v_2^{} & \cdots & v_n^{}\end{bmatrix} $
이 때 $v_i^{*}$는 $v_i$의 켤레복소수(conjugate)입니다.
Dirac notation
벡터 간의 연산을 보다 정의하기 앞서, 양자 역학에서 널리 쓰이는 Dirac notation에 대해 알아보도록 하겠습니다. 앞서 표기한 열벡터는 다음과 같이 쓸 수도 있습니다.
$ \mathbf{v} = \left\vert \mathbf{v} \right> $
이 열벡터는 “ket-$v$”라 불립니다. 이의 adjoint는 다음과 같습니다.
$ \left< \mathbf{v} \right\vert = \mathbf{v}^{\dagger}$
이 벡터는 “bra-$v$”라 불립니다. 합쳐서 말하면 “bra-ket”으로, 괄호를 의미하는 bracket과 흡사합니다. 실제로 LaTeX에서 \bra, \ket 등으로 해당 표기법을 사용할 수 있습니다. 이 표기법은 양자 역학 관련하여 많이 사용됩니다.
Inner product
$\mathbb{C}^n$의 두 벡터 $\mathbf{u}$와 $\mathbf{v}$의 내적(inner product)은 $\left< \mathbf{u} \vert \mathbf{v} \right>$으로 표기하며, 다음과 같이 정의됩니다.
$ \left< \mathbf{u} \vert \mathbf{v} \right> = \mathbf{u}^{\dagger}\mathbf{v} = \begin{bmatrix} u_1^{} & u_2^{} & \cdots & u_n^{}\end{bmatrix} \begin{bmatrix} v_1 \ v_2 \ \vdots \ v_n\end{bmatrix} = u_1^{}v_1 + u_2^{}v_2 + \cdots u_n^{}v_n $
inner product는 임의의 $\mathbf{u}, \mathbf{v},\mathbf{w} \in \mathbb{C}^n$에 대해 다음 세 성질을 만족합니다.
- $\left< \mathbf{v} \vert \mathbf{v} \right> \geq 0$이며, $\left< \mathbf{v} \vert \mathbf{v} \right> = 0 \iff \left\vert \mathbf{v} \right> = \mathbf{0}$.
- $\left< \mathbf{u} \vert \mathbf{v} \right> = (\left< \mathbf{v} \vert \mathbf{u} \right>)^*$.
- 임의의 복소수 $\alpha_0$, $\alpha_1$에 대해 $\left< \mathbf{u} \vert \alpha_0 \mathbf{v} + \alpha_1 \mathbf{w} \right> = \alpha_0 \left< \mathbf{u} \vert \mathbf{v} \right> + \alpha_1 \left< \mathbf{u} \vert \mathbf{w} \right> $. (선형성)
벡터의 norm은 $\vert\vert \left\vert \mathbf{v} \right> \vert\vert$으로 표기하며, $\sqrt{\left< \mathbf{v} \vert \mathbf{v} \right>}$와 같습니다. norm이 1인 벡터를 단위 벡터(unit vector)라 합니다.
Outer product
$\mathbb{C}^n$의 두 벡터 $\mathbf{u}$와 $\mathbf{v}$의 외적(outer product)은 $\left\vert \mathbf{v} \right> \left< \mathbf{u} \right\vert$으로 표기하며, 다음과 같이 정의됩니다.
$ \left\vert \mathbf{v} \right> \left< \mathbf{u} \right\vert = \mathbf{v}\mathbf{u}^{\dagger} = \begin{bmatrix} v_1 \ v_2 \ \vdots \ v_n\end{bmatrix} \begin{bmatrix} u_1^{} & u_2^{} & \cdots & u_n^{}\end{bmatrix} = \begin{bmatrix} v_1 u_1^ & v_1 u_2^* & \cdots & v_1 u_n^* \ v_2 u_1^* & v_2 u_2^* & \cdots & v_2 u_n^* \ \vdots & \vdots & \ddots & \vdots \ v_n u_1^* & v_n u_2^* & \cdots & v_n u_n^* \end{bmatrix}$
결과가 크기 $n \times n$의 행렬이 되었습니다.
두 벡터의 outer product는 뒤에 나올 텐서곱(tensor product, Kronecker product)의 특수한 꼴입니다.
Matrix
크기 $ m \times n $의 행렬(matrix)은 $m$개의 행에 각각 $n$개의 복소수가 있는 구조입니다.
$ M = \begin{bmatrix} a_{11} & a_{12} & \cdots & a_{1n} \ a_{21} & a_{22} & \cdots & a_{2n} \ \vdots & \vdots & \ddots & \vdots \ a_{m1} & a_{m2} & \cdots & a_{mn} \end{bmatrix}$
행렬의 합과 행렬의 곱, 그리고 항등행렬 $I$에 대한 설명은 생략하겠습니다.
몇몇 특수한 조건을 만족하는 행렬들은 따로 부르는 명칭이 있습니다.
- inverse : 행렬 $A$의 역행렬(inverse)은 $A^{-1}$로 표기하며, $AA^{-1} = A^{-1}A = I$를 만족합니다. 역행렬은 존재하지 않을 수도 있으나, 존재하면 유일합니다.
- adjoint : 행벡터처럼, $a_{ij} \mapsto a_{ji}^*$의 대응관계를 통해 만들어지는 행렬입니다. 행렬 $M$의 adjoint는 (vector와 흡사하게) $M^{\dagger}$로 표기합니다.
- unitary : 행렬 $U$가 $UU^{\dagger} = U^{\dagger}U = I$를 만족할 때, 즉 $U^{-1} = U^{\dagger}$일 때 unitary라고 합니다. unitary matrix는 벡터에 곱해도 벡터의 norm이 유지되는 특성이 있습니다. 양자 컴퓨팅에서는 unitary matrix를 많이 다루게 됩니다.
- Hermitian : 행렬 $M$이 $M = M^{\dagger}$일 때 Hermitian이라 합니다.
Tensor product
크기 $m \times n$ 의 배열 $M$과 $p \times q$의 배열 $N$의 텐서곱(tensor product)은 $M \otimes N$으로 표기하며, 다음과 같은 $mp \times nq$의 행렬로 정의됩니다.
$\begin{align} M \otimes N &= \begin{bmatrix} M_{11} & \cdots & M_{1n} \ \vdots & \ddots & \vdots \ M_{m1} & \cdots & M_{mn} \end{bmatrix} \otimes \begin{bmatrix} N_{11} & \cdots & N_{1q} \ \vdots & \ddots & \vdots \ N_{p1} & \cdots & N_{pq} \end{bmatrix}\ &= \begin{bmatrix} M_{11} \begin{bmatrix} N_{11} & \cdots & N_{1q} \ \vdots & \ddots & \vdots \ N_{p1} & \cdots & N_{pq} \end{bmatrix} & \cdots & M_{1n} \begin{bmatrix} N_{11} & \cdots & N_{1q} \ \vdots & \ddots & \vdots \ N_{p1} & \cdots & N_{pq} \end{bmatrix}\ \vdots & \ddots & \vdots \ M_{m1} \begin{bmatrix} N_{11} & \cdots & N_{1q} \ \vdots & \ddots & \vdots \ N_{p1} & \cdots & N_{pq} \end{bmatrix} & \cdots & M_{mn} \begin{bmatrix} N_{11} & \cdots & N_{1q} \ \vdots & \ddots & \vdots \ N_{p1} & \cdots & N_{pq} \end{bmatrix}\end{bmatrix} \end{align} $
$\left\vert \mathbf{v} \right>$에 자기 자신의 텐서곱을 $n$번 한 것을 $\left\vert \mathbf{v} \right> ^{\otimes n}$로 표기합니다. $\left\vert \mathbf{v} \right> \in \mathbb{C}^2$라면, $\left\vert \mathbf{v} \right> ^{\otimes n} \in \mathbb{C}^{2^n}$입니다.
Qubit
고전 체계에서 정보를 담는 단위는 비트(bit)는 0 또는 1의 두 가지 상태에 있을 수 있습니다. 양자 체계에서 정보를 담는 단위는 큐빗(qubit)인데, 0과 1의 상태가 중첩(superposition)되어 있습니다. 0이라는 상태와, 1이라는 상태가 말 그대로 겹쳐있음을 의미한다. 이 상태는 단위 벡터 $\begin{bmatrix} \alpha \ \beta \end{bmatrix} \in \mathbb{C}^2$로 표현이 됩니다. 예를 들면 다음과 같은 벡터들이 올바른 상태의 예시입니다.
$ \begin{bmatrix} 1 \ 0 \end{bmatrix},\begin{bmatrix} 0 \ 1 \end{bmatrix}, \begin{bmatrix} \frac{1}{\sqrt{2}} \ \frac{1}{\sqrt{2}} \end{bmatrix}, \begin{bmatrix} \frac{1}{\sqrt{2}} \ \frac{-1}{\sqrt{2}} \end{bmatrix}, \begin{bmatrix} \frac{-1}{\sqrt{2}} \ \frac{i}{\sqrt{2}} \end{bmatrix}$
이 중 $\begin{bmatrix} 1 \ 0 \end{bmatrix}$과 $\begin{bmatrix} 0 \ 1 \end{bmatrix}$는 이 상태의 기저(basis)가 될 수 있습니다. 기저에 대한 상세한 논의는 하지 않을 것이나, 임의의 단위 벡터를 이 두 벡터의 선형결합으로 표현할 수 있다는 성질은 알아두시면 좋습니다. 무한히 많은 벡터쌍이 기저가 될 수 있지만 계산의 편의상 이 두 벡터를 선택하는 경우가 많으며, 때문에 computational basis라고 불립니다. 이 두 벡터들은 각각 $\left\vert 0 \right>$, $\left\vert 1 \right>$로 표기합니다. 특히 이 기저는 orthonormal하기 때문에 $\left<0 \vert 1 \right> = \left<1 \vert 0 \right> = 0$이랑 $\left<0 \vert 0 \right> = 1, \left<1 \vert 1 \right>=1$이 성립합니다.
그러므로 임의의 큐빗의 중첩 상태는 다음과 같이 표현할 수 있습니다.
$ \left\vert \psi \right> = \alpha \left\vert 0 \right> + \beta \left\vert 1 \right> = \begin{bmatrix} \alpha \ \beta \end{bmatrix} $
Measurement
양자 컴퓨팅에서 큐빗은 기본적으로 $\left\vert 0 \right>$과 $\left\vert 1 \right>$의 중첩상태이지만, 중첩되어 있는 상태에서 관측(measurement)을 하게 될 경우 상태가 $\left\vert 0 \right>$ 또는 $\left\vert 1 \right>$으로 붕괴(collapse)합니다. 이 때 각 상태의 관측확률은 각각 $\vert \alpha \vert ^2$, $\vert \beta \vert^2$입니다. 관측 결과가 확률적이라는 이 당연한 사실이 양자 컴퓨팅의 핵심입니다.
computational basis의 특성상, $\vert \alpha \vert ^2 + \vert \beta \vert ^2 = 1$입니다. 흥미롭게도 $\alpha$와 $\beta$가 복소수이기 때문에, 부호를 바꾸거나 $i$를 곱해도 확률이 변화하지 않습니다.
Bloch Sphere
양자의 상태는 Bloch Sphere라는 구 위에 표현할 수 있습니다.
$ \begin{align} \left\vert \psi \right> &= a_0 \left\vert 0 \right> + a_1 \left\vert 1 \right> \ &= \cos\frac{\theta}{2} \left\vert 0 \right> + e^{i\phi} \sin\frac{\theta}{2} \left\vert 1 \right> \ &= cos\frac{\theta}{2} \left\vert 0 \right> + (\cos\phi + i\sin\phi) \sin\frac{\theta}{2} \left\vert 1 \right> \end{align} $
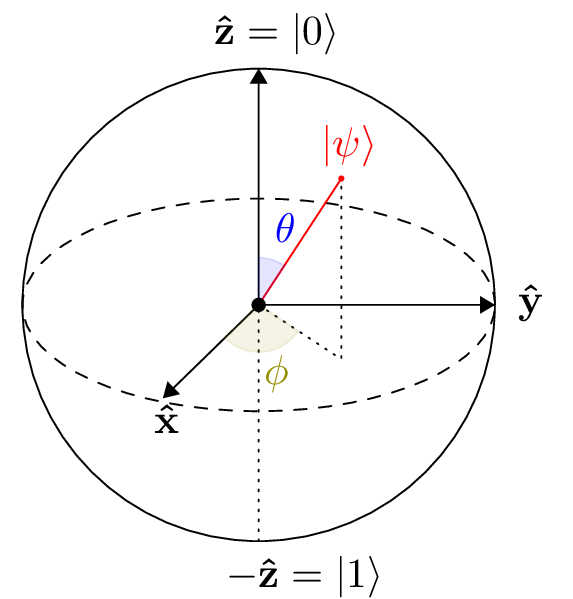
밑에 나올 수많은 quantum gate의 정당성은 Bloch sphere에서 대응되는 관계를 통해 증명할 수 있습니다. 두 기저 사이의 각도가 $\pi/2$가 아닌 $\pi$라는 점이 특기할만 합니다.
Quantum Register
큐빗이 한 개 있는 것보다는 여러 개 있는 게 아무래도 더 좋지 않을까요? 큐빗이 $n$개가 있으면 관측 가능한 상태가 $2^n$개 생깁니다. 즉, 기저 벡터가 $2^n$개 있는 상태입니다.
$ \left\vert \psi \right> = \sum_{i=0}^{2^n-1} a_i \left\vert i \right> $
예를 들어 $n = 2$이면 $ \left\vert \psi_2 \right> = a_0 \left\vert 00 \right> + a_1 \left\vert 01 \right> + a_2 \left\vert 10 \right> + a_3 \left\vert 11 \right> $로 쓸 수 있습니다. 풀어서 쓰면
$ \left\vert \psi_2 \right> = a_0 \begin{bmatrix} 1 \ 0 \ 0 \ 0 \end{bmatrix} + a_1 \begin{bmatrix} 0 \ 1 \ 0 \ 0 \end{bmatrix} + a_2 \begin{bmatrix} 0 \ 0 \ 1 \ 0 \end{bmatrix} + a_3 \begin{bmatrix} 0 \ 0 \ 0 \ 1 \end{bmatrix} $
입니다. 그리고 각 상태를 관측할 확률의 합이 1이 되어야 하므로 $ \sum_{i=0}^{2^n-1} \vert a_i \vert^2 = 1$이 성립합니다.
매번 $2^n$개나 되는 값을 쓸 수 없으므로, 텐서곱으로 줄여서 표기하는 경우가 많습니다. 예를 들어
$\left\vert 0 \right> \otimes \left\vert 1 \right> = \left\vert 01 \right> = \begin{bmatrix} 0 & 1 & 0 & 0 \end{bmatrix}^T $
와 같이 표기합니다.
Quantum Gates
XOR과 AND같은 logical gate가 종종 논리 회로에서 사용되는 것처럼, quantum gate도 상태를 변화시키는 절차입니다. 이 quantum gate는 행렬로 표기되는데, unitary한 특성을 지닙니다. 때문에 모든 quantum gate는 역연산이 가능합니다. Bloch sphere에서 보면 회전변환과 대칭으로 해석할 수 있습니다.
Hadamard Operation
Hadamard operation $H$는 다음과 같습니다.
$ H = \dfrac{1}{\sqrt{2}}\begin{bmatrix} 1 & 1 \ 1 & -1 \end{bmatrix} = \dfrac{\left\vert 0 \right> + \left\vert 1 \right>}{\sqrt{2}} \left< 0 \right\vert + \dfrac{\left\vert 0 \right> - \left\vert 1 \right>}{\sqrt{2}} \left< 1 \right\vert$
수학적으로는 $y$축으로 (시계 방향으로) $\pi/2$만큼 돌리고 $x$축으로 $\pi$만큼 돌리는 과정입니다. 이 회로가 $\left\vert 0 \right>$과 $\left\vert 1 \right>$에 사용되면 어떻게 될까요?
$\begin{align} H \left\vert 0 \right> &= \dfrac{\left\vert 0 \right> + \left\vert 1 \right>}{\sqrt{2}} \left< 0 \vert 0 \right> + \dfrac{\left\vert 0 \right> - \left\vert 1 \right>}{\sqrt{2}} \left< 1 \vert 0 \right> = \dfrac{\left\vert 0 \right> + \left\vert 1 \right>}{\sqrt{2}} \ H \left\vert 1 \right> &= \dfrac{\left\vert 0 \right> + \left\vert 1 \right>}{\sqrt{2}} \left< 0 \vert 1 \right> + \dfrac{\left\vert 0 \right> - \left\vert 1 \right>}{\sqrt{2}} \left< 1 \vert 1 \right> = \dfrac{\left\vert 0 \right> - \left\vert 1 \right>}{\sqrt{2}}\end{align}$
computational basis가 균일한 확률분포의 중첩으로 변환됩니다. 즉, $H \left\vert 0 \right>$과 $H \left\vert 1 \right>$ 모두 $\left\vert 0 \right>$과 $\left\vert 1 \right>$의 관측 확률이 $1/2$로 같아집니다. $H$는 Hermitian이기 때문에 역연산이 자기 자신입니다. 때문에, $H^2 \left\vert 0 \right> = \left\vert 0 \right>$이고 $H^2 \left\vert 1 \right> = \left\vert 1 \right>$입니다.
Pauli-X Gate
Pauli-X gate는 X-gate라는 이름에 걸맞게 기하학적으로는 $x$축 기준으로 $\pi$만큼 돌립니다. $\left\vert 0 \right>$과 $\left\vert 1 \right> $의 진폭이 바뀌기 때문에 0이면 1, 1이면 0인 고전적 NOT gate와 흡사하여 NOT gate라 불리기도 합니다. 수학적으로는 다음과 같습니다.
$X = \begin{bmatrix} 0 & 1 \ 1 & 0 \end{bmatrix}$
Pauli-Y Gate
Pauli-Y gate는 기하학적으로는 $y$축 기준으로 $\pi$만큼 돌립니다. $\left\vert 0 \right>$을 $-i\left\vert 1 \right>$로, $\left\vert 1 \right>$을 $i\left\vert 0 \right>$로 변환합니다.
$Y = \begin{bmatrix} 0 & -i \ i & 0 \end{bmatrix}$
Pauli-Z Gate
Pauli-Z gate는 기하학적으로는 $z$축 기준으로 $\pi$만큼 돌립니다. $\left\vert 0 \right> $은 그대로, $\left\vert 1 \right>$을 $-\left\vert 1 \right>$로 변환합니다.
$Z = \begin{bmatrix} 1 & 0 \ 0 & -1 \end{bmatrix}$
Phase Gate
Z-gate는 진폭의 위상만 건드리는데, 이 특성은 Z-gate의 일반화인 phase gate에도 적용됩니다.
$R_\phi = \begin{bmatrix} 1 & 0 \ 0 & e^{i\phi} \end{bmatrix}$
Z-gate는 $\phi = \pi$인 경우로 볼 수 있습니다. 그 외에 자주 사용되는 gate는 $\phi = \pi/2$인 S-gate나 $\phi = \pi/4$인 T-gate 등이 있습니다.
$S = \begin{bmatrix} 1 & 0 \ 0 & i \end{bmatrix}$
$T = \begin{bmatrix} 1 & 0 \ 0 & e^{i\pi/4} \end{bmatrix}$
universal quantum gates
양자컴퓨터가 물리적으로 X, Y, Z에 대응하는 회로를 전부 만들지는 않습니다. 일반 컴퓨터를 생각해보면, universal logic gate가 있습니다. 즉, 임의의 logical operation을 유한한 횟수의 universal logic gate로 나타낼 수 있습니다. NAND가 대표적입니다. NAND로 NOT, AND, OR, XOR, MUX 등을 모두 표현할 수 있습니다.
문제는 양자 컴퓨터의 경우, 수학적으로 임의의 quantum operation을 유한한 횟수로 표현할 수 있는 유한한 quantum gate의 집합이 존재하지 않습니다. logical bit의 경우 입력 상태도 2가지, 출력 상태도 2가지지만, 양자 상태는 입력 상태가 무한히 많으며, 출력 상태도 무한히 많기 때문입니다. 때문에 양자 컴퓨팅에서 universal이라는 용어는 고전 컴퓨팅보다는 살짝 약하게, 특정 오차 내로 임의의 quantum gate를 유한한 종류의 gate를 유한번 이용하여 표현할 수 있음을 의미합니다. 대표적인 예시로 Hadamard gate $H$와 $T$-gate가 있으며, 구현체마다 조금 더 회로를 (물리적으로) 구현하여 쓰기도 합니다.
Controlled Quantum Gates
양자 컴퓨팅은 ‘controlled operation’이란 걸 할 수 있습니다. 고전 컴퓨팅으로 치면 if문과도 흡사한데, control qubit의 상태가 모두 $\left\vert 1 \right>$일 때만 큐빗에 operation을 진행하는 기능입니다. bit와는 달리 qubit은 상태의 중첩이 가능하므로 controlled operation을 이용해 다양한 동작을 할 수 있습니다.
대표적인 예시로 controlled not이 있습니다. control qubit을 $\left\vert c \right>$, target qubit을 $\left\vert t \right>$라고 할 때 $\left\vert t \right> \mapsto \left\vert t \oplus c \right>$라 할 수 있습니다. 행렬로 표현하면 다음과 같습니다.
$CNOT = \begin{bmatrix}1 & 0 & 0 & 0 \ 0 & 1 & 0 & 0 \ 0 & 0 & 0 & 1 \ 0 & 0 & 1 & 0 \end{bmatrix}$
NOT 뿐만 아니라 임의의 unitary operation $U$을 controlled처럼 적용할 수 있습니다.
$U_{control} = \begin{bmatrix}I & O \ O & U\end{bmatrix}$
qubit이 $n$개 있어도 비슷하게 적용할 수 있습니다.
양자 컴퓨팅의 효과 및 한계
가끔씩 기사나 블로그 등에서 양자 컴퓨팅은 고전 컴퓨팅보다 모든 면에서 우세하고, 결과적으로 고전 컴퓨팅을 몰아낼 것이라고 주장하기도 합니다. 이는 사실이 아닙니다. 양자 컴퓨팅은 고전 컴퓨팅보다 모든 면에서 우세하지 않으며, 양자 컴퓨팅에서도 동일한 시간 복잡도를 보이는 분야도 있을 뿐더러, 양자 법칙으로 인해 물리적 구현이 힘든 상황입니다. 양자 컴퓨팅의 효과와 한계를 살펴보도록 하겠습니다.
시간 복잡도 이론
시간복잡도 이론에서 $\mathsf{P}$는 결정론적 튜링 머신이 다항 시간 안에 해결할 수 있는 모든 결정 문제의 집합입니다. 예를 들어 소수 판정법, 그래프의 최대 매칭(의 결정 문제) 등이 있습니다. $\mathsf{NP}$는 결정론적 튜링 머신이 다항 시간 안에 답을 검증할 수 있는 모든 결정 문제의 집합입니다. traveling salesman problem, boolean satisfiability problem 등이 그 예시입니다. $\mathsf{NP}$의 문제들 중 가장 ‘어려운’ 문제들을 $\mathsf{NP}$-complete라고 하고, $\mathsf{NPC}$라 합니다. $\mathsf{P} \subset \mathsf{NP}$임은 당연하지만, 과연 $\mathsf{P} = \mathsf{NP}$일까요? 이가 바로 밀레니엄 7대 난제 중 하나인 “P vs NP” 문제로, 아직 증명도 반증도 되지 않았으나 $\mathsf{NP}$에 있는 문제를 효율적으로 풀 수 있는 알고리즘이 아직 발견되지 않았기에 일반적으로 $\mathsf{P} \neq \mathsf{NP}$라 여겨집니다. $\mathsf{BPP}$는 간단히 설명하면, 비결정론적 튜링 머신이 다항 시간 안에 $2/3$ 이상의 확률로 답을 구할 수 있는 문제들의 집합입니다. 증명은 되지 않았으나 학자들은 $\mathsf{P} = \mathsf{BPP}$일 것으로 보고 있습니다.
양자 컴퓨팅은 관측이 ‘확률적’이기 때문에, 비슷하게 $\mathsf{BQP}$가 있습니다. 다항 시간안에 양자 컴퓨터가 $2/3$ 확률 이상으로 답을 구할 수 있는 결정 문제들의 집합입니다. 역시 아직 증명되지는 않았으나 학자들은 $ \mathsf{P} \subset \mathsf{BQP}$일 것으로 보고 있습니다. 즉, 고전 컴퓨터가 다항 시간 안에 해결할 수 없으나 양자 컴퓨터로 비결정론적으로 다항 시간 안에 해결할 수 있는 결정 문제가 있다고 예상됩니다.
양자 컴퓨팅 연구 진척도
더 많은 예시들이 [3]에 있으니 일독을 권장드립니다.
- Grover’s Algorithm : 무작위로 배열된 $N$개의 값 중 특정 조건을 만족하는 값을 $O(\sqrt{N})$에 찾을 수 있습니다. 밑에 열거될 알고리즘에 빈번히 사용됩니다.
- Shor’s Algorithm : 수 $N$을 소인수분해하는데 $O((\log N)^3 (\log \log N))$의 시간복잡도로 할 수 있습니다.
- 행렬 $A \times B = C$의 참거짓 판별을 최악에 $O(n^{5/3})$,평균적으로 $O(n^{5/3}/\min(w, \sqrt{n})^{1/3})$에 계산할 수 있습니다 ($w$는 다른 값의 개수). 고전 컴퓨팅에서는 $O(n^{2.376})$이 최선입니다.
- 정점 $n$개 간선 $m$개의 그래프의 minimum spanning tree를 $O(\sqrt{mn})$에 찾을 수 있습니다. 고전 컴퓨팅에서는 Borůvka’s algorithm의 $O(m \log n)$이 최선입니다.
- 정점 $n$개 간선 $m$개의 그래프의 maximum flow를 $O(n^{7/6} \sqrt{m})$에 찾을 수 있습니다. 고전 컴퓨팅에서는 $O(nm)$이 최선입니다.
- 그 외 다양한 최적화 문제를 해결할 수 있고, 양자역학을 시뮬레이션할 수 있습니다.
Entanglement
두 qubit $\psi$, $\phi$가 $\left\vert 00 \right>$ 상태에 있다고 합시다. $\psi$에 Hadamard gate를 적용하고, 이 qubit을 control qubit으로 삼아 $\phi$와 같이 controlled NOT gate을 거치면 양자 상태를 다음과 같이 만들 수 있습니다.
$\psi \otimes \phi = \begin{bmatrix} 1/\sqrt{2} \ 0 \ 0 \ 1/\sqrt{2}\end{bmatrix} = \dfrac{\left\vert 00 \right> + \left\vert 11 \right>}{\sqrt{2}}$
이 상태는 특이하게도, 두 양자의 텐서곱으로 표현할 수 없습니다. 즉, 이 상태는 두 양자를 쪼개서 따로 설명할 수가 없습니다. 이런 상태를 ‘양자 얽힘(quantum entanglement)’이라고 합니다. 두 양자가 이렇게 얽혀 있을 때 관측을 하면 가능한 상태가 $\left\vert 00 \right>$이나 $\left\vert 11 \right>$밖에 없기 때문에 두 양자가 같은 상태로 붕괴하게 됩니다. 이론상 물리적 거리에 제약이 없고, $2^n$개의 상태를 $n$개의 양자에 담을 수 있는 이유이기도 하기에 물리적으로도, 컴퓨터 공학적으로도 대단히 흥미로운 성질입니다. 연구에 의하면 entanglement가 없는 양자 컴퓨터는 고전 컴퓨터에 비해 나을 게 없다고 합니다 [5].
Infidelity and decoherence
IBM Q Experience에서 구현된 5개의 qubit 양자 컴퓨터의 구조는 흔히 생각하는 fully-connected가 아닙니다. 모든 큐빗이 서로 연결되어서 직접적으로 controlled operation을 할 수 있는 구조도 아닙니다. 물론 수학적으로 임의의 상태에서도 control이 가능하게 설계되어 있지만, 하드웨어 구현은 이론과는 다르다는 점을 알아야 합니다.
하드웨어 설계만 문제가 아닙니다. 양자 컴퓨팅을 할 때 필연적으로 다양한 소음(noise)가 양자 상태에 침범합니다. gate infidelity와 decoherence(결잃음)가 두 예시입니다.
gate infidelity는 사용자가 만든 quantum gate가 물리적으로 구현된 quantum gate에 완벽히 들어맞지 않기 때문에 누적되는 오차를 뜻합니다. 다양한 큐빗이 서로 연결되어 있을 때는 더 심해집니다. 때문에 알고리즘상 multi-qubit gate의 개수를 줄이는 과정이 필요합니다. decoherence는 시간이 지남에 따라 양자 컴퓨터가 ‘양자성’을 잃고 고전 컴퓨터처럼 행동하게 된다는 원리입니다. 때문에 알고리즘의 수행 횟수가 중요한 문제가 됩니다.
현재 기술로는 양자 상태가 decoherence가 일어나기 전까지 한 10~100 µs 정도로 유지시킬 수 있다고 합니다 [6]. 1-qubit gate가 20 ns, 2-qubit gate가 40 ns, 관측이 300 ns ~ 1 µs 정도 걸린다고 하니 연산을 무한정 할 수 없는 셈입니다 [7].
No-cloning theorem
양자 컴퓨팅은 강력하지만, 그 위력에는 한계가 있습니다. No-cloning theorem이란, 임의의 미지 양자 상태를 다른 독립적인 양자에 그대로 복사할 수 없다는 정리입니다. 철학적인 논의로 보일 수 있지만 물리학적으로도 증명되어 있습니다. 때문에 어떠한 양자 상태를 복제할 때는 필연적으로 오차가 발생할 수밖에 없습니다. 양자역학에서 정보는 공짜가 아니며, 정보를 얻으면 이에 상응하는 효과가 양자계에 영향을 미치게 됩니다.
결론
양자컴퓨팅에 대한 막연한 이해가 되셨을지 모르겠습니다. 하지만 이 포스팅을 통해 양자컴퓨팅이 어떤 수학적 근간을 이루고 있고, 만능 black-box가 아니라는 사실만 알아도 충분하다고 생각합니다. 보다 관심이 있으신 분들은 밑의 참고 문헌의 [1-3]을 보시길 바랍니다. 공부하면서 많은 도움이 되었습니다.
이후 속편으로는 가장 확장성이 높은 양자 알고리즘일 Grover’s Algorithm에 대한 분석을 진행해보고자 합니다.
참고 문헌
- Microsoft QDK - Quantum computing concepts
- Strubell, E. (2011). An introduction to quantum algorithms. COS498 Chawathe Spring, 13, 19. (링크)
- Coles, P. J., Eidenbenz, S., Pakin, S., Adedoyin, A., Ambrosiano, J., Anisimov, P., … & Gunter, D. (2018). Quantum algorithm implementations for beginners. arXiv preprint arXiv:1804.03719.
- IBM Quantum Experience - Docs and Resources : Decoherence
- Guifré Vidal. Efficient classical simulation of slightly entangled quantum computations. Physical review letters, 91(14):147902, 2003.
- M. Reagor, W. Pfaff, C. Axlineet al., “Quantum memory withmillisecond coherence in circuit qed,”Phys. Rev. B, vol. 94, p.014506, Jul 2016. [Online]. Available: https://link.aps.org/doi/10.1103/PhysRevB.94.014506
- X. Fu, L. Riesebos, M. A. Rolet al., “eQASM: An executable quantuminstruction set architecture,” inHPCA 2019, Feb 2019, pp. 224–237.