최대 이분 매칭에 관한 몇 가지 정리
bipartite-matching , minimum-vertex-cover , maximum-independent-set , minimum-path-cover , maximum-antichain
이분 그래프(Bipartite Graph)에서의 최대 매칭(Maximum Matching)은 최대 유량(Maximum Flow)과 같습니다. 이 글에서는 위와 같이 최대 유량과 최대 이분 매칭에 관한 기본적인 문제를 해결 할 수 있는 분들을 위해 최대 이분 매칭에 관한 대표적인 정리를 예제와 함께 다룹니다. 구성은 아래와 같습니다.
- Minimum Vertex Cover - BOJ 1867 돌멩이 제거
- Maximum Independent Set - BOJ 11014 컨닝 2
- Minimum Path Cover - BOJ 1671 상어의 저녁식사
- Maximum Anti-Chain - BOJ 13441 마법의 나무
Minimum Vertex Cover
Vertex Cover란 그래프에서 정점들의 부분집합으로, 그래프의 모든 간선은 Vertex Cover의 정점 중 하나 이상에 인접해야 합니다. 모든 정점을 선택하는 것 또한 Vertex Cover이며 Minimum Vertex Cover는 그중에서도 집합의 크기가 가장 작은 것을 의미합니다.
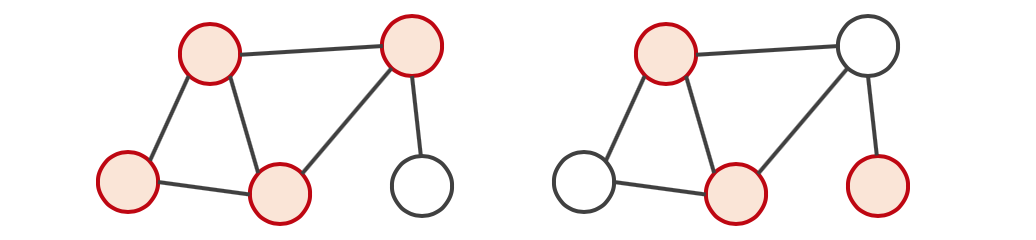
일반적인 그래프의 Minimum Vertex Cover는 다항시간 안에 풀 수 없지만 쾨닉의 정리(Konig’s Theorem)를 보면 이분 그래프에서의 $|Minimum Vertex Cover|$는 $|Maximum Matching|$과 같다고 증명되어 있습니다.
관련 문제로 제법 유명한 BOJ 1867 - 돌멩이 제거 문제를 봅시다. $N \times N$ 격자 위에 K개의 돌멩이가 있을 때, 최소한의 행과 열을 선택해 모든 돌멩이를 제거하는 문제입니다. 여기에서 우리가 할 수 있는 일은 행이나 열을 선택하는 일이고, 이 선택을 최소화 해야 합니다.
하나의 돌멩이를 제거하기 위해서는 돌멩이가 있는 행이나 열 중 하나만 선택해도 됩니다. 문제를 풀기 위해 관점을 바꿔봅시다. 각 행과 열을 정점으로, 돌멩이를 간선으로 보고 돌멩이가 위치한 좌표 $(r, c)$에 대해 $r->c$ 간선을 추가합니다. 이렇게 되면 모든 행이 왼쪽에 있고 모든 열이 오른쪽에 있는 이분 그래프가 만들어집니다.
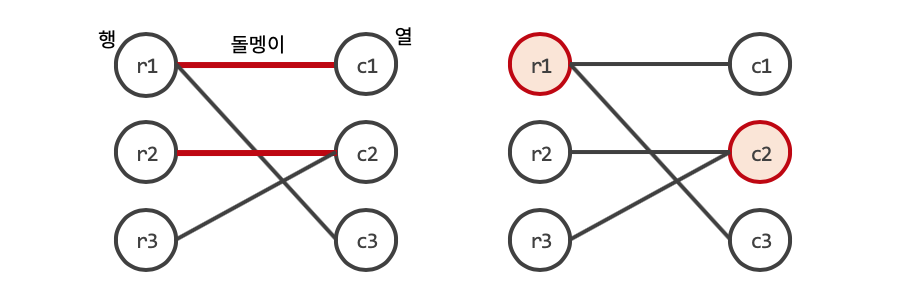
우리가 원하는 것은 최소한의 열과 행을 선택해 모든 돌멩이를 제거하는 것입니다. 열과 행이 정점이고 돌멩이가 간선이니 이는 최소한의 정점을 선택해 모든 간선을 덮는 Minimum Vertex Cover와 같습니다. 또한 쾨닉의 정리에 의해 이는 만들어진 이분 그래프의 최대 매칭과 같아집니다. 이렇게 이분 그래프로 나타낼 수 있고 그래프의 모든 간선을 사용해야 하는 문제가 있다면 Minimum Vetex Cover로 접근할 수 있습니다.
+) 만약 Minimum Vertex Cover의 개수와 함께 집합을 구성하는 정점을 구해야한다면 Bipartite Matching을 구한 뒤 아래의 정의에 따라 구할 수 있습니다.
- $L$ : 왼쪽에 배치된 정점 집합
- $R$: 오른쪽에 배치된 정점 집합
- $X$: $L$에서 출발하여 alternating path를 통해 방문할 수 있는 정점 집합
- $Y$: $R$에서 출발하여 alternating path를 통해 방문할 수 있는 정점 집합
- Minimum Vertex Cover: $(L∩Y)∪(R∩X)$
Maximum Independent Set
Independent Set이란 그래프에서 정점들의 부분집합으로, Independent Set의 어떤 두 정점도 하나의 간선을 통해 열결되지 않는 집합입니다. 그중 집합의 크기가 가장 큰 것을 Maximum Independent Set이라고 합니다.
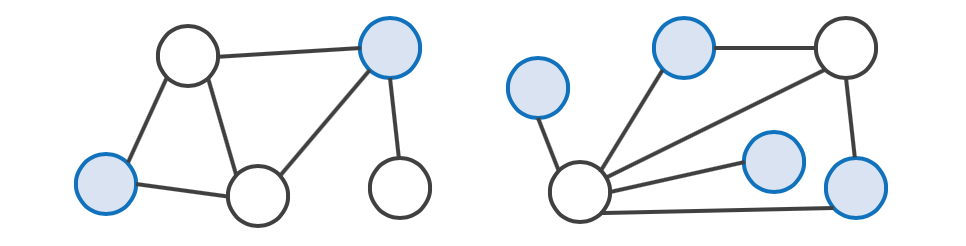
역시 일반적인 그래프에서 Maximum Independent Set을 구하는 것은 다항시간 안에 풀 수 없지만, 이분 그래프에서 Minimum Vertex Cover를 생각해보면 집합에 포함된 정점쌍을 연결하는 간선이 없어야하는 Maximum Independent Set은 Minimum Vertex Cover의 여집합이 되는 것을 알 수 있습니다.
따라서 이분 그래프의 정점 개수를 $V$라고 할 때, 다음과 같은 식이 성립합니다. $V = |Minimum Vertex Cover| + |Maximum Independent Set|$
BOJ 11014 - 컨닝 2 문제를 봅시다. NxM 장애물이 포함된 격자에 다른 사람을 컨닝하지 못하도록 하며 최대한 많은 사람을 배치하는 문제입니다. 이 문제를 어떻게 Maximum Independent Set에 적용할 수 있을까요?
원하는 답이 가장 많은 사람을 컨닝하지 못하도록 배치하는것이니, 사람을 정점으로 하고 컨닝을 할 수 있다는 관계를 간선으로 나타내보면 어떨까요?
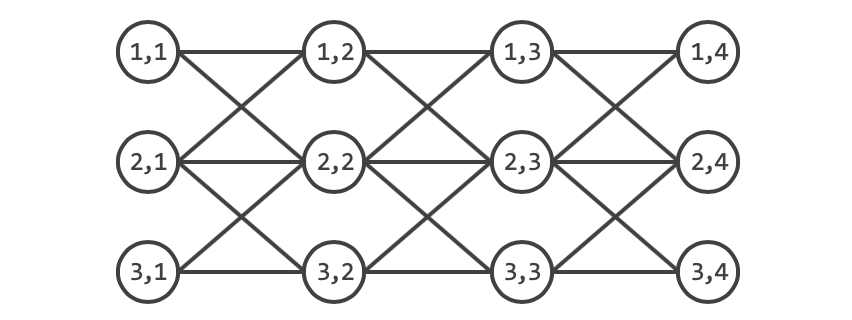
와 신기해라, 홀수열 사이와 짝수열 사이에는 연결이 없기 때문에 이분 그래프로 표현 된다는 걸 알 수 있습니다. 따라서 홀수열을 왼쪽으로, 짝수열을 오른쪽으로 하고 컨닝 관계를 간선으로 하는 이분 그래프가 있을 때 우리가 원하는 답은 컨닝 관계인 간선을 공유하는 두 정점을 동시에 선택하지 않으면서 최대한 많은 정점을 선택하는 Maximum Independent Set이 되며 이는 $(V - |Minimum Vertex Cover|)$이므로 정점 수에서 최대 매칭을 빼면 구할 수 있습니다.
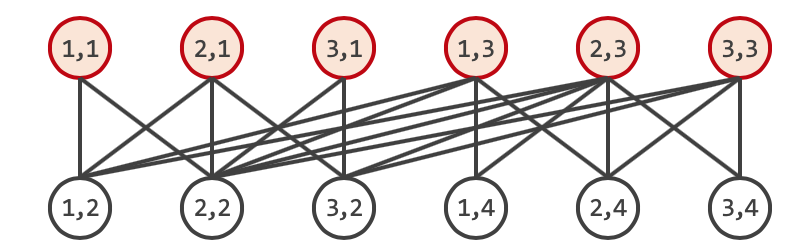
위는 장애물이 존재하지 않는 경우라 당연히 홀수 열에만 학생을 앉히는 답이 나오지만 장애물이 있다면 달라지겠죠?
Minimum Path Cover
Path Cover란 Directed Acyclic Graph(DAG)에서 각 Path가 어떤 정점도 공유하지 않으면서 모든 정점이 하나의 Path에 속하는 Path의 집합입니다. Path는 그래프상의 간선을 따라 이동할 수 있는 경로입니다. 이때 Minimum Path Cover란 Path의 개수가 가장 적은 것을 의미합니다.
BOJ 1671 - 상어의 저녁식사 문제를 봅시다. 각 상어의 능력치를 통해 먹이사슬이 정해질 때, 살아남을 수 있는 상어의 최솟값을 구하는 문제입니다. 예제를 그림으로 나타내면 아래와 같습니다. 간선은 하위 포식자에서 상위 포식자를 연결합니다.
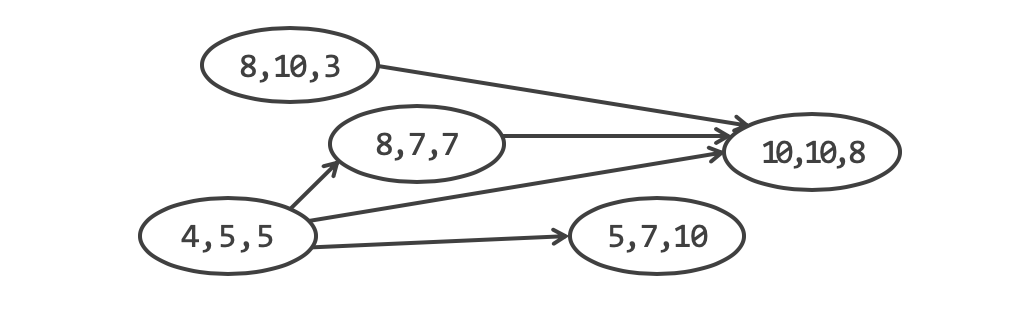
문제에서 한 상어는 최대 두 상어만 먹을 수 있다고 합니다. 그렇다면 이 제한을 더 줄여서 한 상어는 최대 하나의 상어만 먹을 수 있다면 어떨까요? 한 상어가 최대 하나의 상어만을 먹을 때 마지막에 살아남는 상어의 수는 겹치지 않게 연결할 수 있는 먹이사슬의 수와 같습니다. 거기서 우리는 이 문제를 Minimum Path Cover 문제로 바꿔볼 수 있습니다.
모든 먹이사슬(Path) 겹치는 정점이 없어야 합니다. 따라서 모든 정점은 indegree가 1 이하이고 outdegree가 1이하이며, indegree가 0인 정점은 Path의 시작이고 outdgree가 0인 정점은 Path의 끝이며 다른 모든 degree는 1이 됩니다.
이를 이용해 우리는 DAG를 이분 그래프로 바꿀 수 있습니다. 모든 정점을 두 개로 나눠봅시다. 어떤 정점 $v$에 대해 $v1$은 $v$의 outdegree를, $v2$는 $v$의 indegree를 뜻하도록 하고 $v1$을 이분 그래프의 왼쪽, $v2$를 이분 그래프의 오른쪽에 배치합니다. 이때 $u->v$ 간선이 존재하면 $u1->v2$ 간선을 연결합니다.
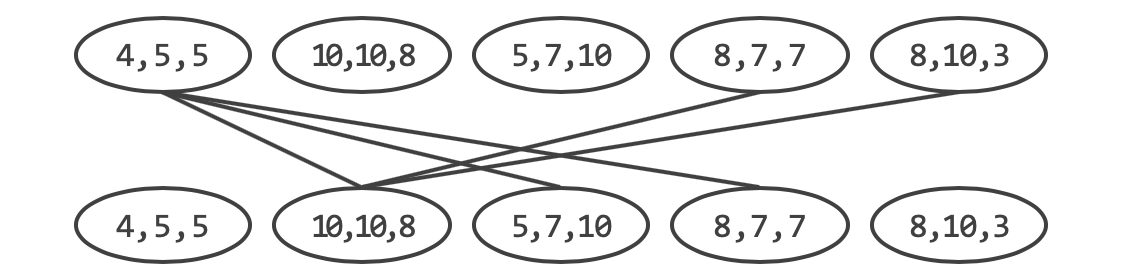
해당 이분 그래프에서 구한 최대 이분 매칭을 $M$개라고 하면 이는 모든 Path에 속하는 간선을 총 개수입니다. 기존 정점의 개수가 $V$개라고 할 때 Path에 속하는 간선이 $M$이라는 것은 Path의 개수가 $(V - M)$개라는 것과 같습니다. Path의 마지막 정점은 살아남은 상어를 뜻하고, 해당 상어를 제외한 상어들은 모두 outdegree를 하나씩 가지니까요. 이때 $M$은 최대 매칭이기 때문에 $(V - M)$은 Minimum Path Cover가 됩니다.
여기서 원래 문제로 돌아갑시다. 원래 문제에서는 한 상어는 최대 두 상어를 먹을 수 있습니다. 이 말은 패스에 속한 상어는 최대 2의 indegree를 가질 수 있다는 의미입니다. 따라서 우리는 indegree를 뜻하는 오른쪽 정점을 두 배 해주면 문제의 요구와 같은 그래프를 만들 수 있고, 답은 $(N - M)$이 됩니다.
Maximum Anti-Chain
Anti-Chain(반사슬)이란 방향 그래프 정점 부분집합으로 반사슬 내의 어떤 두 정점도 위상이 없음을 만족해야 합니다. 예를 들어 {a, b, c, d}가 있고 a->b, c->b, b->d의 간선으로 이루어진 그래프에서 a와 c는 서로 위상이 없기 때문에 {a, c}는 반사슬입니다. {b, c}는 c->b가 존재하므로 반사슬이 아닙니다. 마찬가지로 {c, d}도 c->b->d의 패스가 정의되므로 반사슬이 아닙니다. 이러한 부분집합 중 가장 큰 것을 Maximum Anti-Chain이라고 합니다.
딜워스 정리(Dilworth’s Theorem)를 보면 방향 그래프에서 Maximum Anti-Chain의 크기는 Minimum Path Cover와 같다고 증명되어 있습니다.
BOJ 13441 - 마법의 나무 문제를 봅시다. 나무 하나를 마법의 나무로 만들면 관계가 있는 나무들이 연쇄적으로 보호를 받습니다. 마법의 나무이면서 다른 나무에게 보호받지 못하는 나무를 최대로 하는 문제입니다.
어떤 나무를 마법의 나무로 만들면 해당 나무가 좋아하는 나무를 비롯해 그 나무들이 좋아하는 나무들이 연쇄적으로 보호받게 됩니다. 우리는 각 나무를 마법의 나무로 만들었을 때 어떤 나무가 보호받게 될지를 알 수 있습니다.
마법의 나무지만 보호받지 못하는 나무의 수를 최대화하기 위해서 마법의 나무로 바꿀 나무들의 집합을 생각해봅시다. 하나를 마법의 나무로 바꾸면 그에 관련된 모든 나무는 같은 집합에 들어올 수 없습니다. 따라서 우리는 서로 위상 관계가 없는 나무만을 정답으로 포함할 수 있으며 이를 최대화하는 곧 최대 반사슬을 의미합니다. 이는 Minimum Path Cover로 구할 수 있습니다.
Minimum Path Cover를 구하기 위해 각 정점을 이번에도 둘로 쪼갭니다. 어떤 정점 $v$에 대해 $v1$은 자신이 보호받게 되었을 때 보호할 나무들을 향해 outdegree를, $v2$는 보호받았을 때 자신을 보호해주는 나무에서 오는 indegree를 연결합니다. 여기서 구한 최대 매칭을 $M$이라고 하면 마법의 나무이면서 보호받지 못하는 나무의 최댓값은 $(N - M)$이 됩니다.
마치며
매칭과 관련된 것이 아니라도 이분 그래프에는 재미있는 성질이 많습니다. 그중에는 위에서 다룬 것처럼 서로 닿아있어서 이게 저거라서 이런지 저게 이거라서 저런지 헷갈리는 것들도 있습니다. 사실 저도 종종 다른 의미로 해석해서 풀어내곤 하는데 이런 분들께 도움이 된다면 좋겠습니다.
혹시 본 포스팅 내용 중 잘못된 내용이 있다면 Acka1357@gmail.com 으로 말씀해주세요 :)