2D Segment Tree
안녕하세요, 이번 글에서는 2D Segment Tree 에 대해 알아보도록 하겠습니다.
Segment Tree에 관한 기초 지식
2D Segment Tree를 이해하기 위해서는 Persistent Segment Tree 포스팅 때와 비슷하게 Segment Tree에 대한 이해가 선행되어야 합니다. Segment Tree가 무엇인지, 혹은 Dynamic Segment Tree가 무엇인지 모르고 있다면 먼저 링크를 타고 그 부분을 공부한 후에 오시는 것을 추천드립니다.
Bottom-Up 방식의 Segment Tree
Segment Tree를 구현하는 방법으로는 Top-Down 방식과 Bottom-Up 방식이 있습니다. 이전 글에서는 Top-Down 방식만을 설명했으나 2D Segment Tree에서는 Bottom-Up 방식을 통해 메모리에서 이득을 보는 경우가 있어 이번 글에서는 Bottom-Up 방식을 설명하도록 하겠습니다.
Bottom-Up 방식은 Top-Down 방식과 비슷하게 미리 각 노드가 특정 구간을 대표하는 이진 트리에서 연산이 이루어집니다. 이 이진트리는 리프가 $n$개이고 인덱스가 적절하게 붙어있어 정확히 $2n$의 공간이 필요합니다.
Top-Down 방식은 재귀적인 구조로 인해 함수 호출이 다수 발생하고 메모리가 최대 $4n$만큼 필요한 반면 Bottom-Up 방식은 반복문을 돌면서 동작하고 메모리가 정확히 $2n$만큼 필요하기 때문에 실행 속도와 메모리 모두 Bottom-Up 방식보다 Top-Down 방식이 우수합니다. 그러나 lazy propagation의 경우, Bottom-Up 방식에서도 처리가 가능하긴 하지만 Top-Down 방식이 더 직관적으로 이해가 쉬워 저는 lazy propagation이 필요하면 Top-Down으로, 그렇지 않으면 Bottom-Up으로 구현하는 것을 선호합니다.
5, 4, 3, 2, 1, 0 이라는 배열로 Bottom-Up 방식의 Segment Tree를 구축하면 아래와 같습니다.
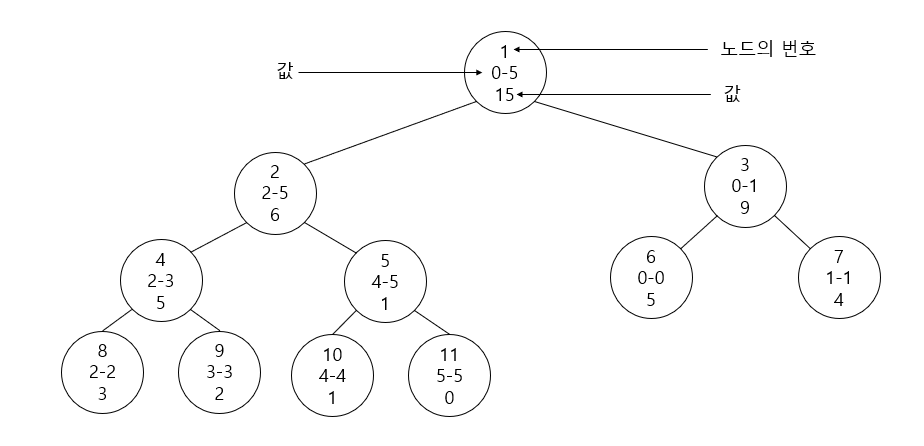
index가 정해지는 것이 Top-Down 방식과 약간 차이가 있는데, 0-indexed 기준으로 $k$번째 원소는 $n+k$번 노드에 대응이 됩니다.
Init의 경우에는 $n$번 노드부터 $2n-1$번 노드까지 0, 1, 2, .. 번째 배열의 원소 값을 다 넣어둔 후 $n-1$번 노드부터 $1$번 노드까지 자식 두 개의 합을 대입하도록 함으로서 구현할 수 있습니다.
Update의 경우에는 $n+k$번 노드에서 시작해 1번 노드에 도달할 때 까지 부모로 계속 올라가면서(=2를 나누면서) 만나는 모든 노드에 대해 값을 갱신해주면 되기에 굉장히 간단합니다.
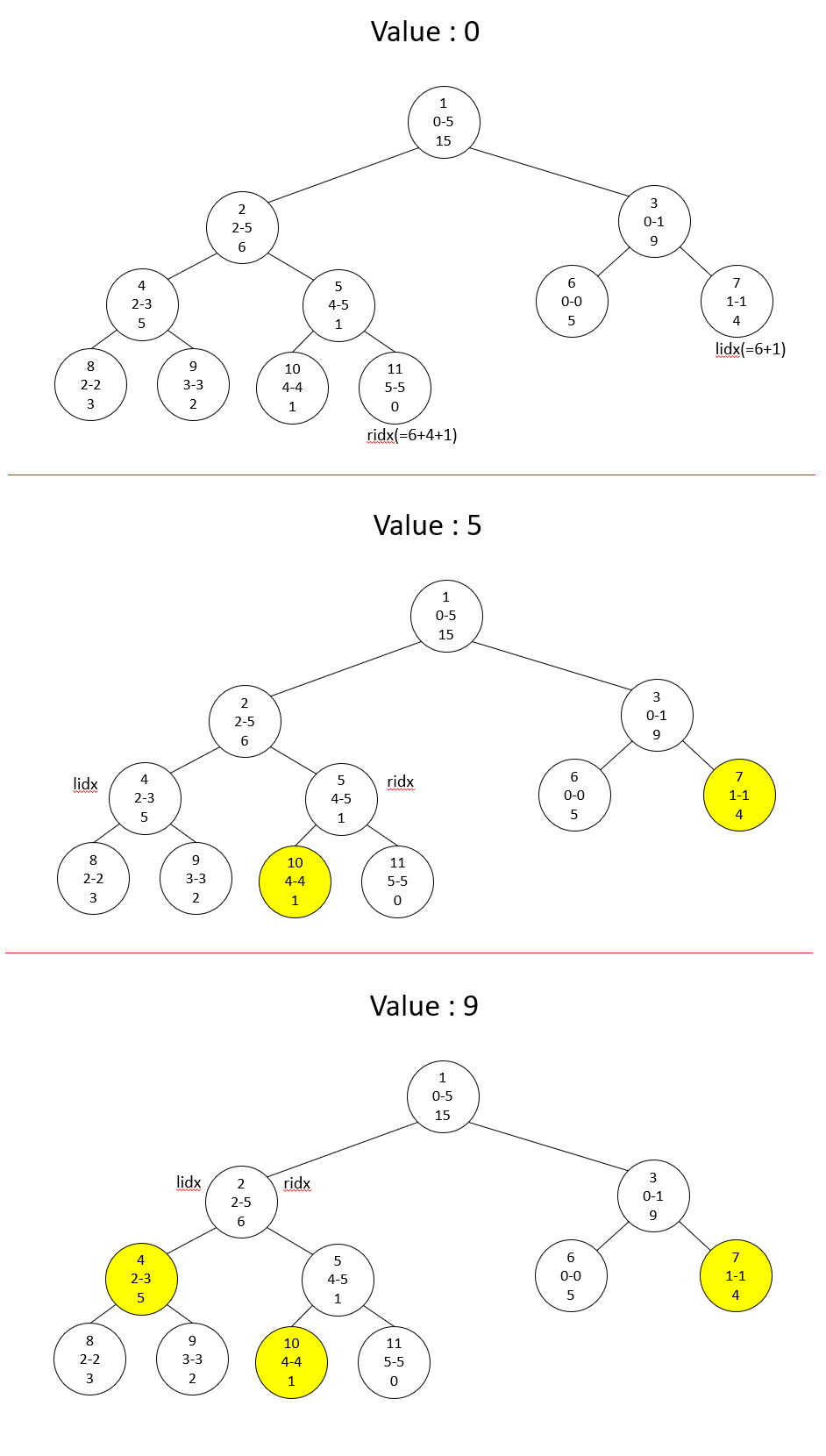
Query의 경우에는 $l$번째부터 $r$번째까지의 원소의 합을 구한다고 할 때 lidx를 $n+l$번 노드에, ridx를 $n+r+1$번 노드에 둔 후 lidx < ridx일 때 까지 부모로 올라가는 방식으로 구현합니다.
이 때, lidx가 오른쪽 자식 노드일 경우 해당 노드의 값을 더하고 lidx의 값을 1 증가시켜주고, ridx가 오른쪽 자식 노드일 경우 ridx의 값을 1 뺀 후 해당 노드의 값을 더하면 됩니다. 이후 부모로 올라갑니다. 말로 풀어쓰면 조금 헷갈릴 수 있는데 아래의 그림을 참고해주세요. lidx 에서부터 ridx-1 까지의 값이 더해져야 한다는 점에 집중하면(즉 ridx의 경우 exclusive한 범위라는 점에 집중하면) 이해에 도움이 될 것입니다.
제가 주로 쓰는 Segment Tree의 클래스는 아래와 같습니다.
class Seg{
public:
int n;
vector<int> a;
Seg(int n):n(n),a(2*n){}
void init(){
for(int i = n-1; i > 0; i--) a[i] = a[i<<1]+a[i<<1|1];
}
void upd(int i, int val){ // add val on i-th element
for(a[i+=n] += val; i > 1; i >>= 1) a[i>>1] = a[i] + a[i^1];
}
int query(int l, int r){
int ret = 0;
for(l += n, r += n+1; l < r; l >>= 1, r >>= 1){
if(l&1) ret += a[l++];
if(r&1) ret += a[--r];
}
return ret;
}
};
확실히 Top-Down 방식보다 구현 난이도도 낮고 공간도 적게 씀을 알 수 있습니다.
2D Segment Tree란?
2D Segment Tree는 이차원 배열에서 특정 노드의 Update와 구간의 Query를 $lg^2n$에 처리할 수 있는 자료구조입니다. 각 노드가 Segment Tree인 Segment Tree를 만든다는 충격적인 아이디어를 통해 구현이 가능합니다. 4*4 배열에서의 예시를 그림으로 들면 아래와 같습니다.
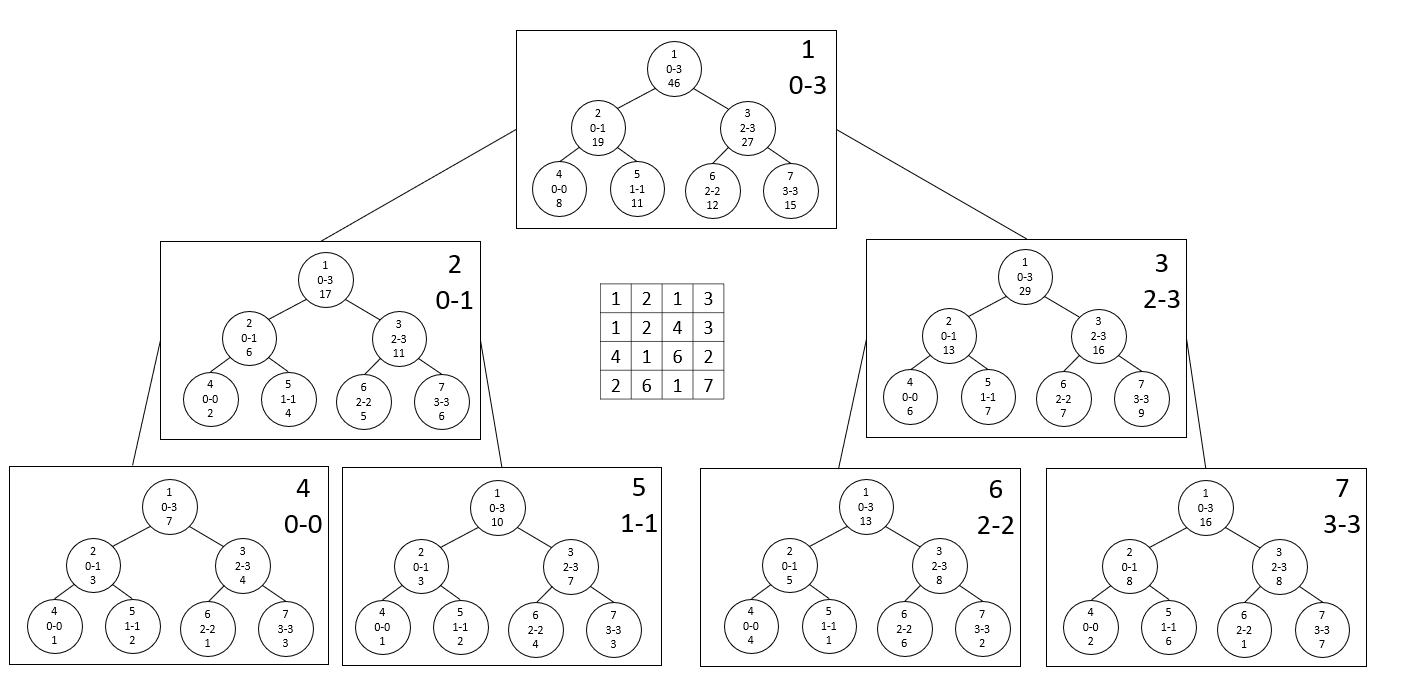
굉장히 난해한 모양이지만 곰곰히 이해를 하려고 해본다면 크게 어렵지는 않습니다. 네모난 모양의 노드는 각 row 자체를 원소로 생각한 노드이고, 네모난 모양의 노드가 담고 있는 Segment Tree는 자신이 담당하는 row들의 구간 내에서 일반적인 1차원 Segment Tree를 만든 것입니다.
N*M 크기의 배열에서 Update, Query 모두 최대 $lgNlgM$개의 원소에 대한 처리가 필요합니다. 아래의 예시를 참고해보세요.
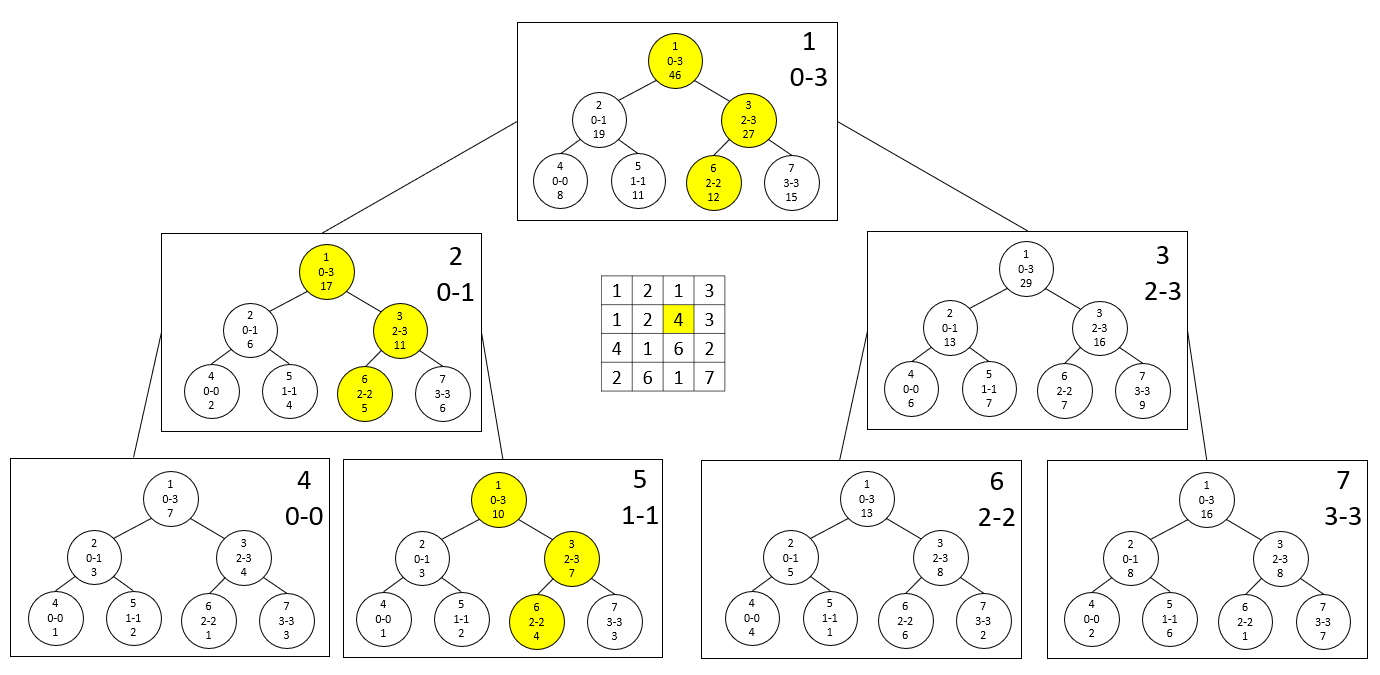
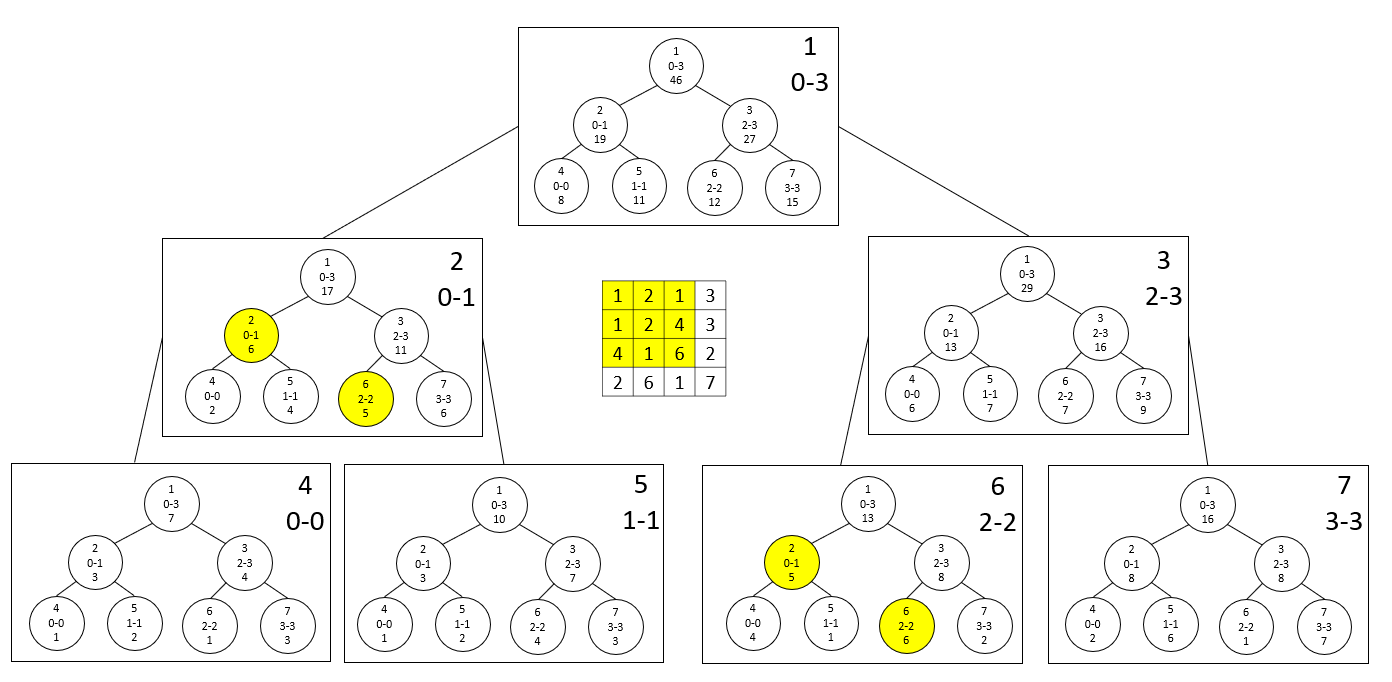
미리 각 배열의 원소가 주어져있을 때 Init을 하기 위해서는 바깥 Segment Tree 기준 자식 둘의 합을 계속 가져오는 방식으로 구현이 이루어집니다. 아래는 2D Segment Tree의 예시 코드입니다.
// 0-indexed
class Seg2D{
public:
int n;
vector<vector<int>> a;
Seg2D(int n) : n(n), a(2*n,vector<int>(2*n)){}
// n*n인 2차원 vector를 인자로 보내야 함
void init(vector<vector<int>>& val){
for(int i = 0; i < n; i++){
for(int j = 0; j < n; j++)
a[i+n][j+n] = val[i][j];
}
// 바깥 Segment Tree의 leaf node인 Segment들에 대한 처리
for(int i = n; i < 2*n; i++){
for(int j = n-1; j > 0; j--) a[i][j] = a[i][j<<1]+a[i][j<<1|1];
}
// 바깥 Segment Tree의 leaf node가 아닌 Segment들에 대한 처리
for(int i = n-1; i > 0; i--){
for(int j = 1; j < 2*n; j++){
a[i][j] = a[i<<1][j] + a[i<<1|1][j];
}
}
}
// (x, y)의 값을 val로 변경
void upd(int x, int y, int val) {
a[x+n][y+n] = val;
// 바깥 Segment Tree의 leaf에 대한 처리
for(int i = y+n; i > 1; i >>= 1) a[x+n][i>>1] = a[x+n][i] + a[x+n][i^1];
// 바깥 Segment Tree의 leaf node가 아닌 Segment들에 대한 처리
for(x = x+n; x > 1; x >>= 1){
for(int i = y+n; i >= 1; i >>= 1){
a[x>>1][i] = a[x][i]+a[x^1][i];
}
}
}
int query1D(int x, int y1, int y2){
int ret = 0;
for(y1 += n, y2 += n+1; y1 < y2; y1 >>= 1, y2 >>= 1){
if(y1 & 1) ret += a[x][y1++];
if(y2 & 1) ret += a[x][--y2];
}
return ret;
}
// sum of l-th to r-th element(0-indexed)
int query(int x1, int y1, int x2, int y2) {
int ret = 0;
for(x1 += n, x2 += n+1; x1 < x2; x1 >>= 1, x2 >>= 1){
if(x1&1) ret += query1D(x1++, y1, y2);
if(x2&1) ret += query1D(--x2, y1, y2);
}
return ret;
}
};
이 코드를 이용해 BOJ 11658번 - 구간 합 구하기 3을 풀어보았습니다. 코드를 확인해보세요.
이 문제를 2D BIT를 이용해서 풀어도 해결이 가능하고 실행속도와 메모리 모두 Segment Tree보다 좋지만 BIT의 특성상 구간의 최댓값 구하기와 같이 역연산이 존재하지 않는 연산에 대해서는 해결이 불가능하다는 단점이 있습니다.
메모리 절약 방법
현재의 2D Segment Tree 구현은 N*M 배열에서 $O(NM)$의 공간이 필요합니다. 이것만 해도 그럭저럭 어렵지만, 실제 2D Segment Tree 문제들은 더 흉악한 경우가 많습니다.
대표적으로 IOI 13 GAME(BOJ 링크), SEERC 2018 Points and Rectangles(BOJ 링크)의 경우 $N, M$이 최대 $10^9$입니다.
물론 Offline 쿼리라고 한다면 좌표압축을 통해 $N, M$을 최대 쿼리의 갯수 만큼 줄일 수 있긴 하지만 그렇다고 해도 쿼리가 많게는 25만개씩 되는 상황에서는 여전히 $O(NM)$이 불가능합니다.
Top-Down 방식과 Bottom-Up 방식에서 모두 메모리 절약 기법을 적용할 수 있는데 각각의 장단점이 있기 때문에 두 경우를 모두 살펴보도록 하겠습니다.
Top-Down 방식
사실 Top-Down 방식에서 2D Segment Tree를 어떻게 만들면 되는지 글에서 아직 언급하지 않았지만 기본적인 흐름 자체는 비슷하기 때문에 별도로 설명을 하지는 않겠습니다.
Top-Down 방식에서 메모리를 절약하는 방법은 저번 포스팅에서 Dynamic Segment Tree에서 설명한 것과 비슷한 방식으로 진행합니다. Update를 진행해나갈 때 필요한 노드만 그때그때 만들어가는 방식으로 구현을 하면 되고, Query의 경우 잘 생각해보면 노드가 없을 경우 굳이 만들지 않아도 됨을 알 수 있습니다.
IOI 13 GAME 문제에 대한 정답 코드를 확인해보세요. 참고로 원래 IOI에서 나왔을 때에는 Online Query로 해결을 해야해서 지금과 상황이 살짝 다르긴 합니다. Online Query일 경우 코드 내에서 rszR, rszC를 활용한 것과 달리 인덱스의 시작과 끝을 10^9로 잡아야 합니다.
문제는 Top-Down 방식이 Bottom-Up 방식보다 메모리를 많이 차지한다는 단점으로 인해 지금처럼 Update가 최대 22,000번이 아니라 더 많은 경우에는 메모리 초과가 발생할 수 있습니다. Points and Rectangles 문제를 Top-Down 방식으로 구현했을 경우 메모리 초과를 피할 수가 없었습니다. (코드)
Bottom-Up 방식
위에서 나왔던 Bottom-Up 방식을 잘 생각해보면 바깥 Segment Tree에 노드가 $2n$개 필요하고, 각 노드는 $n$개의 원소를 Segment Tree로 만든 구조, 즉 $2n$개의 int를 가지고 있는 Segment Tree이기 때문에 $O(n^2)$의 공간이 필요했습니다.
Bottom-Up에서 공간을 절약하는 핵심 아이디어는 바깥 Segment Tree는 $2n$의 노드가 필요하지만 각 노드가 $n$개의 원소를 다 가지고 있을 필요가 없다는 점입니다.
다시 위의 그림을 보며 Upd(1,2)와 Query(0,0,2,2)가 호출되는 상황을 생각해봅시다.
바깥 Segment Tree의 1번 노드는 2번 원소에 대한 Segment Tree만 구축하고 있으면 질의를 처리할 수 있습니다.
2번 노드는 0번과 2번 원소에 대한 Segment Tree만 구축하고 있으면 질의를 처리할 수 있습니다.
5번 노드는 2번 원소에 대한 Segment Tree만 구축하고 있으면 질의를 처리할 수 있습니다.
6번 노드는 0번과 2번 원소에 대한 Segment Tree만 구축하고 있으면 질의를 처리할 수 있습니다.
나머지 노드들은 아무 정보도 가지고 있지 않아도 상관이 없습니다.
즉 바깥 Segment Tree의 특정 노드를 볼 때, Upd, Query 과정에서 필요한 원소만을 가지고 선별적으로 Segment Tree를 구축해두어도 아무런 문제가 없습니다.
그렇기에 우선 fakeUpd, fakeQuery 메소드를 이용해 바깥 Segment Tree의 각 노드에서 어떤 원소들이 필요한지를 저장해둔 다음 prepare 메소드로 갯수를 파악해 Segment Tree의 크기를 알맞게 조절한 후 Upd, Query를 다시 실행하면 됩니다. 제가 사용하는 템플릿 코드는 아래와 같습니다.
// 0-indexed
// 반드시 fake를 먼저 다 해준 후에 prepare()를 호출하고 원래 upd, query를 호출해야 함
class Seg2D{
public:
int n;
vector<vector<int>> a;
vector<vector<int>> used;
Seg2D(int n) : n(n), a(2*n), used(2*n) {}
void fakeUpd(int x, int y, int val){
for(x += n; x >= 1; x >>= 1) used[x].pb(y);
}
void fakeQuery(int x1, int y1, int x2, int y2){
for(x1 += n, x2 += n+1; x1 < x2; x1 >>= 1, x2 >>= 1){
if(x1&1){ used[x1].pb(y1); used[x1++].pb(y2); }
if(x2&1){ used[--x2].pb(y1); used[x2].pb(y2); }
}
}
void prepare(){
for(int i = 0; i < 2*n; i++){
if(!used[i].empty()){
sort(used[i].begin(), used[i].end());
used[i].erase(unique(used[i].begin(),used[i].end()),used[i].end());
}
used[i].shrink_to_fit();
a[i].resize(used[i].size()*2);
}
}
void upd(int x, int y, int val) {
for(x += n; x >= 1; x >>= 1){
int i = lower_bound(used[x].begin(),used[x].end(),y)-used[x].begin() + used[x].size();
for(a[x][i] += val; i > 1; i >>= 1) a[x][i>>1] = a[x][i] + a[x][i^1];
}
}
int query1D(int x, int y1, int y2){
int ret = 0;
y1 = lower_bound(used[x].begin(),used[x].end(),y1)-used[x].begin();
y2 = lower_bound(used[x].begin(),used[x].end(),y2)-used[x].begin();
for(y1 += used[x].size(), y2 += used[x].size()+1; y1 < y2; y1 >>= 1, y2 >>= 1){
if(y1 & 1) ret += a[x][y1++];
if(y2 & 1) ret += a[x][--y2];
}
return ret;
}
// sum of l-th to r-th element(0-indexed)
int query(int x1, int y1, int x2, int y2) {
int ret = 0;
for(x1 += n, x2 += n+1; x1 < x2; x1 >>= 1, x2 >>= 1){
if(x1&1) ret += query1D(x1++, y1, y2);
if(x2&1) ret += query1D(--x2, y1, y2);
}
return ret;
}
};
그런데 이 코드는 Top-Down에서의 상황과는 다르게 Update에 대해서도 일단 공간을 점유하고 있다는 단점이 있습니다. 그래서 IOI 13 Game과 같이 Query가 적으나 Update가 최대 25만번인 상황에서는 도리어 메모리 초과가 발생해버립니다. (코드) 또한 Online Query에서는 사용이 불가능합니다.
그러나 Points and Rectangles 문제와 같이 Update와 Query가 비슷한 빈도로 등장하는 문제에서는 랜덤 입력에 대해 Top-Down 방식은 대략 600-700MB 정도의 메모리를 사용하는 반면 Bottom-Up 방식은 100-150MB 정도의 메모리를 사용하는 차이를 보였습니다.
마무리
2D Segment Tree의 경우 구현도 난해하지만 시간과 메모리의 가늠이 까다로워 무언가 찜찜한 상태로 코딩을 해서 제출을 하고 결과를 보고 수정을 해야하는 경우가 종종 있습니다. 그리고 2D Segment Tree로 풀 수 있을 것 같지만 일반적인 Segment Tree에 Divide and Conquer를 사용해도 해결할 수 있는 경우 또한 종종 있습니다. 위에서 언급한 Points and Rectangles도 2D BIT를 쓰면 1.5초 내외이고 Bottom-Up 2D Segment Tree를 쓰면 2초 내외인 반면 Divide and Conquer를 사용하면 0.5초 내외로 해결이 가능합니다.
그렇기에 2D Segment Tree를 숙달하는 것도 좋지만 2D Segment Tree로 해결이 가능한 문제라고 할지라도 시간과 메모리 제한이 애매하다고 생각이 들 때에는 또 다른 접근 방법이 있는지를 먼저 고민해본 후에 코딩에 들어가는 것도 좋은 전략입니다.