problem solving 1
문제풀이를 하면서 재미있었던 문제를 소개하고자 간단하게 문제 설명과 풀이를 작성해보았습니다.
Min Max Convert (SEERC 2018)
$N (N \leq 100,000)$개의 숫자를 가진 배열 $A, B$가 주어질 때, 2가지 쿼리를 이용하여 $A$ 배열을 $B$ 배열로 만들 수 있으면 해당 쿼리를 출력하고 불가능하면 -1을 출력하는 문제입니다. 그리고 가능한 경우에는 쿼리를 $2*N$ 번 이하로 사용해서 만들어야 합니다.
첫번째 쿼리는 $[a, b]$ 구간의 숫자들을 모두 해당 구간의 최대값으로 변경하는 쿼리고, 두번째 쿼리는 $[a, b]$ 구간의 숫자들을 모두 해당 구간의 최소값으로 변경하는 쿼리입니다.
우선 B의 배열을 보면서 첫번째 수부터 만들어간다고 생각해봅시다.
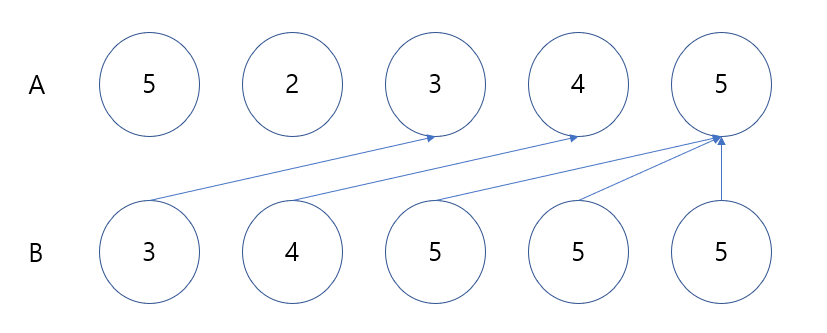
그럼 해당 숫자 $x$ 를 $A$ 배열에서 가장 먼저나오는 수를 찾고나면 그 수를 이용해서 첫번째 인덱스의 숫자도 $x$ 로 바꿀 수 있습니다. 해당 수가 $A$ 배열에서 $i$ 번째에서 처음 발견되었다고 하면 $[1, i-1]$ 구간의 모든 수가 $x$ 보다 크거나 같으면 $[1, i]$에 최소값으로 바꾸는 쿼리를 날리고, 반대로 작거나 같으면 $[1, i]$에 최대값으로 바꾸는 쿼리를 날리고 큰수, 작은수가 모두 있다면 $[1, i-1]$에 최소값으로 바꾸는 쿼리를 날리고 $[1, i]$에 최대값으로 바꾸는 쿼리를 날리면 첫번째 인덱스를 $x$ 로 바꿀 수 있습니다.
이런 경우에 $A$ 배열의 첫번째 수를 $3$ 으로 만들기 위해 $[1, 2]$ 에 최소값으로 바꾸는 쿼리를 날리고 $[1, 3]$ 에 최대값으로 바꾸는 쿼리를 날리면 $3, 3, 3, 4, 5$ 이 되어 첫번째 인덱스는 3이 됩니다.
이제 B배열의 $2$ 번째 수를 만든다고 생각해봅시다.
이전에 첫번째 수를 만들때 $[1, i]$ 구간의 숫자를 모두 같은수로 만들었기 때문에 $2$ 번째 수를 찾을때는 $i$ 보다 크거나 같은 인덱스에서 찾아야 합니다. 그리고 찾았다면 위와 같은 방식으로 숫자를 바꿔나가면 됩니다.
이 과정에서 해당 숫자가 발견되지 않는다면 그 경우는 불가능한 경우입니다.
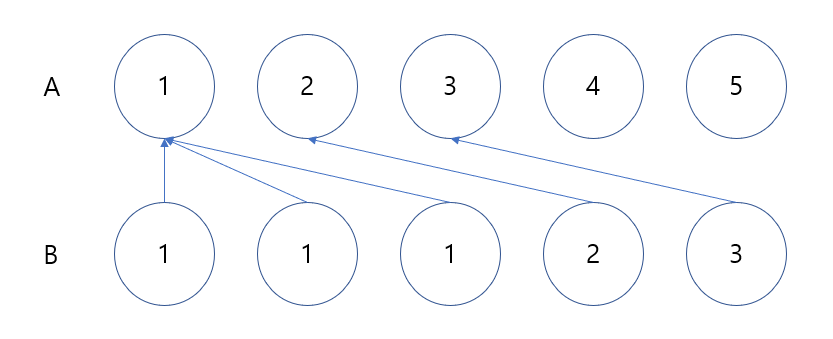
여기서 주의해야 할점은 $B$ 배열의 $j$ 번째 숫자가 $A$ 배열에 $i$ 번째 숫자에 발견되었다고 할 때 $j$ 가 $i$ 보다 크다면 순서대로 진행하면 안되고 역전되는 경우를 모두 모아서 $j$ 가 큰 숫자부터 만들어 가야합니다.
위와 같은 경우에 차례대로 $1, 2, 3, 4, 5$ 번째 숫자를 만들어 간다고 하면 $3$ 번째 숫자까지 만들고 나면 A 배열은 $[1, 1, 1, 4, 5]$ 가 되어 $2$ 와 $3$ 이 사라지게 되어 불가능하게 되므로 반대로 역전되는 경우인 $2, 3, 4, 5$ 번째 숫자들은 모아서 $5, 4, 3, 2$ 순으로 만들어가야 합니다.
위 과정을 투포인터를 이용해서 구현하면 $O(N)$ 에 구현할 수 있으며 매 인덱스의 숫자를 만들때마다 $1$ 번 혹은 $2$ 번의 쿼리만 사용하므로 $2*N$ 번 이하의 쿼리도 보장이 됩니다.
#include <bits/stdc++.h>
using namespace std;
int n;
int a[100000];
int b[100000];
int match[100000];
bool rv[100000];
vector<pair<char, pair<int,int>>> ret;
void revSolve(int sj, int ej) {
for(int i = ej-1, j = ej-1; j >= sj; j--) {
int minVal = n+1, maxVal = -1;
while(i > match[j]) {
minVal = min(minVal, a[i]);
maxVal = max(maxVal, a[i]);
i--;
}
if(maxVal == -1) continue;
if(minVal >= b[j])
ret.push_back(make_pair('m', make_pair(i, j)));
else if(maxVal <= b[j])
ret.push_back(make_pair('M', make_pair(i, j)));
else {
ret.push_back(make_pair('m', make_pair(i+1, j)));
ret.push_back(make_pair('M', make_pair(i, j)));
}
}
}
bool solve() {
ret.clear();
memset(rv, 0 ,sizeof(rv));
for(int i = 0, j = 0; j < n; j++) {
while(i < n && a[i] != b[j]) i++;
if(i == n) return false;
match[j] = i;
if(i < j)
rv[j] = true;
}
for(int i = 0, j = 0; j < n; j++) {
if(rv[j]) {
int sj = j;
while(j < n && rv[j])
j++;
revSolve(sj, j);
i = j;
j--;
continue;
}
int minVal = n+1, maxVal = -1;
while(i < match[j]) {
minVal = min(minVal, a[i]);
maxVal = max(maxVal, a[i]);
i++;
}
if(i == j)
i++;
if(maxVal == -1) continue;
if(minVal >= b[j])
ret.push_back(make_pair('m', make_pair(j, i)));
else if(maxVal <= b[j])
ret.push_back(make_pair('M', make_pair(j, i)));
else {
ret.push_back(make_pair('m', make_pair(j, i-1)));
ret.push_back(make_pair('M', make_pair(j, i)));
}
}
printf("%d\n", ret.size());
for(auto& it: ret)
printf("%c %d %d\n", it.first, it.second.first+1, it.second.second+1);
return true;
}
int main() {
scanf("%d", &n);
for(int i = 0; i < n; i++)
scanf("%d", a+i);
for(int i = 0; i < n; i++)
scanf("%d", b+i);
if(solve())
return 0;
printf("-1\n");
return 0;
}
Four Coloring (ACM-ICPC Yokohama 2018)
정점 $n$ 개, 간선 $m$ 개를 가진 평면그래프가 주어집니다. 여기서 정점는 $(x, y)$ 좌표의 $2$차원 격자위에 존재하며 간선은 반드시 $(x1, y1), (x2, y2)$ 을 연결하는 간선이 있다면 $x1 = x2$이거나 $y1 = y2$이거나 $|x1-x2| = |y1-y2|$ 를 만족합니다. 즉, 한 정점은 최대 $8$ 개의 정점과 연결될 수 있습니다.
이러한 조건을 가지는 그래프에서 모든 정점에 최대 $4$ 개의 색을 이용해 칠하여 모든 연결되어 있는 정점의 색을 다르게 해야 합니다.
우선 정점을 $(x, y)$ 페어에 대해서 사전순 정렬을 하고 정점을 차례대로 보면서 색을 칠해간다고 해봅시다. 그러면 연결된 정점중에 최대 $4$개는 이미 칠해져 있을 수 있고 최대 $4$개는 아직 칠해지지 않았을 것입니다. 매번 칠해지지 않은건 생각하지 말고 이미 칠해진 정점과 다른 색을 칠하면 해결할 수 있습니다.
$5$ 개의 색을 이용한다면 그냥 위와 같이 칠하면 되지만 $4$ 개의 색을 이용하여 칠해야 되기 때문에 다른 방법을 생각해야 합니다.
우선 연결되어 있는 정점 색의 종류가 $3$ 개 이하라면 칠해지지 않은 색을 이용하여 칠하면 됩니다.
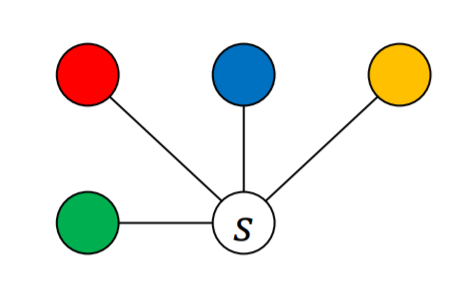
색의 종류가 $4$ 개라면 하나의 색을 아래와 같은 방법으로 바꿀 수 있습니다.
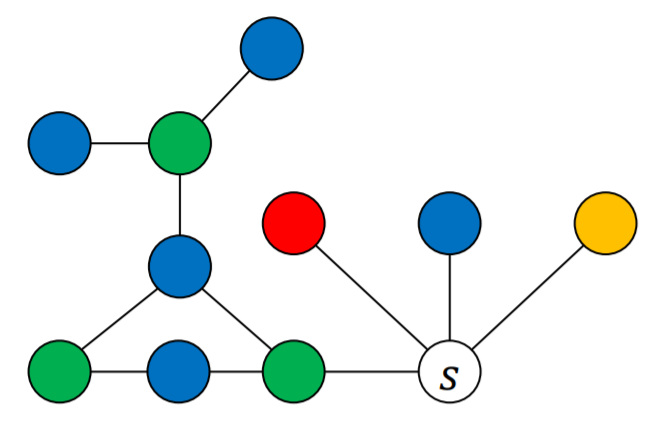
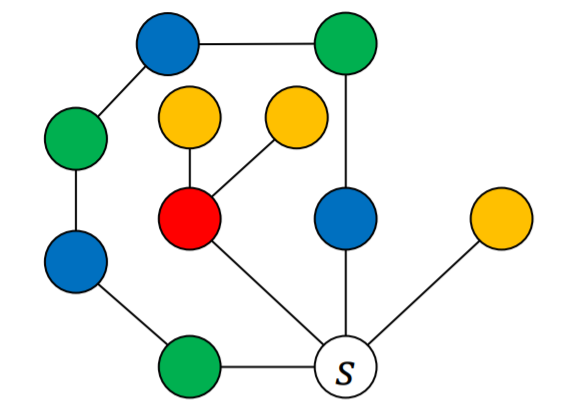
위와 같은 상태에서 초록을 파랑으로 바꾼다고 생각해봅시다.
그러면 초록에서부터 탐색을 하면서 연결되어있는 모든 초록, 파랑색을 반대의 색으로 바꿔야 합니다.
$s$ 에 연결된 초록에서 초록과 파랑만으로 연결된 경로를 통해 s에 연결된 파랑까지 도달할 수 없다면 그냥 초록에서 시작해서 초록, 파랑을 반대색으로 바꾸면 됩니다. 그럼 $s$ 에 연결되어 있는 정점 중에 초록이 없어지게 되므로 $s$ 에 초록을 칠하면 됩니다.
하지만 $s$ 에 연결된 초록, 파랑의 경로가 존재한다면 반대 색으로 바꿔도 초록이 파랑이 되고 파랑이 초록이 되어 전체 색의 개수가 줄지 않아 해결이 되지 않습니다.
하지만 $s$ 에 연결된 초록과 파랑의 경로가 존재한다면 이 그래프는 평면그래프이기 때문에 빨강 정점은 초록 파랑의 경로에 갇히게 됩니다.
그러므로 해당 경우에는 $s$ 에 연결된 빨강과 노랑의 경로는 존재할 수 없습니다.
$s$ 에 연결된 빨강에서 시작해서 빨강과 노랑의 색을 바꿔주면 $s$의 색을 빨강으로 칠할 수 있게 됩니다.
매 정점마다 최대 $(N+M)$번 연산을 하게 되므로 시간복잡도는 $O(N(N+M))$ 가 됩니다.
구현을 할때는 $s$ 에 연결되어 있는 초록 파랑을 연결되어있는지 체크를 하지 말고 우선 초록에서 시작에서 초록, 파랑을 바꾸고 나서 그 뒤에 $s$에 연결된 초록이 있는지 없는지 체크를 하면 좀 더 간단하게 구현할 수 있습니다.
#include <bits/stdc++.h>
using namespace std;
struct point {
int idx, x, y;
point(int idx, int x, int y):idx(idx), x(x), y(y) {}
bool operator <(const point& other) {
return y == other.y ? x < other.x : y < other.y;
}
};
const int MAX = 10001;
int n, m;
int x[MAX], y[MAX];
vector<point> v;
int col[MAX];
vector<int> graph[MAX];
inline int getDir(int i, int j) {
if(y[j] > y[i])
return 4;
if(y[j] == y[i]) {
if(x[j] < x[i])
return 0;
else
return 4;
}
if(x[j] < x[i])
return 1;
if(x[j] == x[i])
return 2;
return 3;
}
struct Pre {
int dir, col, idx;
Pre(int dir, int col, int idx):dir(dir), col(col), idx(idx) {}
bool operator <(const Pre& other) {
return dir < other.dir;
}
};
bool visited[MAX];
void change(int idx, int from, int to) {
visited[idx] = true;
col[idx] = to;
for(int nex: graph[idx])
if(!visited[nex] && col[nex] == to)
change(nex, to, from);
}
int main() {
scanf("%d %d", &n, &m);
for(int i = 1; i <= n; i++) {
scanf("%d %d", x+i, y+i);
v.push_back(point(i, x[i], y[i]));
}
sort(v.begin(), v.end());
while(m--) {
int a, b;
scanf("%d %d", &a, &b);
graph[a].push_back(b);
graph[b].push_back(a);
}
for(auto x: v) {
int i = x.idx;
vector<Pre> pre;
bool check[5] = {0, };
for(int j: graph[i])
if(col[j] != 0) {
pre.push_back(Pre(getDir(i, j), col[j], j));
check[col[j]] = true;
}
bool ok = false;
for(int j = 1; j <= 4; j++)
if(!check[j]) {
ok = true;
col[i] = j;
break;
}
if(ok) continue;
sort(pre.begin(), pre.end());
int temp = pre[0].col;
memset(visited, 0, sizeof(visited));
change(pre[0].idx, pre[0].col, pre[2].col);
col[i] = temp;
if(col[pre[0].idx] == col[pre[2].idx]) continue;
temp = pre[1].col;
change(pre[1].idx, pre[1].col, pre[3].col);
col[i] = temp;
}
for(int i = 1; i <= n; i++)
printf("%d\n", col[i]);
return 0;
}