알고리즘을 이용한 Problem Solving
Lagrange the Chef (Nanjing 2018)
당신은 요리사입니다! 당신이 만들 수 있는 요리는 $10^6$개가 있으며, 손님에게 만들 수 있는 요리 중 $N$개를 코스요리처럼 순서대로 주려 합니다. (고를 수 있는 요리는 중복 가능합니다.) 당신의 식당에 한 손님이 찾아 왔습니다. 이 손님은 매우 특이하여 $X, Y$요리가 연속적으로 나오는 것을 싫어합니다. 즉 $X$다음에 바로 $Y$요리가 나오거나, $Y$다음에 바로 $X$음식이 나오면 불평을 하며 식당을 떠나갑니다. 당신은 식당에 불만이 들어오는 것을 싫어합니다. 따라서, 요리를 하는 순서를 적당히 바꾸어 주려 합니다. 하지만 이미 요리를 하는데 있어서 일정한 순서가 있던 탓에, $i$번째 요리를 다른 순서에 하려면 $1$의 힘이 듭니다. 따라서, 바꿔야 할 순번의 요리 개수를 최소화하면서 손님의 요구를 충족시켜주어야 합니다. 이때 요리의 순서를 적당히 바꿔 손님의 요구를 충족시킬 수 있을 때 드는 힘을 최소로 해주세요! 문제의 제한은 $1 \leq N \leq 5000$, $1 \leq X, Y \leq 10^6$, $1\leq a_i \leq 10^6$입니다.
풀이
우선 a_i배열을 다음과 같이 변환해 줍시다.
$b_i = X if a_i is X$
$b_i = Y if a_i is Y$
$b_i = Z if a_i is neither X nor Y$
그리고 $K = (the number of Z) + 1$이라 합시다. 이렇게 정의할 경우, 다음 조건들의 경우 빠르게 해결할 수 있습니다.
- 만약 모든 $b_i$가 $X$또는 $Y$인 경우, 정답은 0입니다.
- 만약 $X$와 $Y$모두 없다면 정답은 0입니다.
- 만약 $b_i$에 $Z$가 없고, $X$와 $Y$가 모두 존재하는 경우, 항상 만들 수 없습니다.
그러면 이 경우를 빼고 생각해봅시다. 그러면 우리가 만들 수 있는 배열의 형태는 다음과 같을 것입니다.
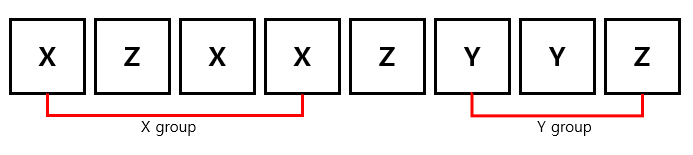
위와 같이 X….XZY…Y와 같이 X와 Y가 Z를 사이에 두고 반복하여 나타나는 형식으로 만들 수가 있을 겁니다. 그러면 이 중 Grouping을 잘 하여 X, Y그룹으로 나누어봅시다. 각 그룹끼리는 붙어있으면 안되며, X그룹 다음에는 하나 이상의 Z와 Y그룹이, Y그룹 다음에는 하나 이상의 Z와 X그룹이 등장하게 하며, X그룹에는 X와 Z만, Y그룹에는 Y와 Z만 등장하게 하도록 합시다. 그러면 여기서 만들 수 있는 총 그룹의 개수는 몇 개일까요? 모든 Z를 미리 빼둔 뒤 각 그룹사이에 Z를 하나씩만 넣으면 되기 때문에 (Z의 개수 + 1)개, 즉 위에서 정의한 K개의 그룹을 만들 수 있을 것입니다.
그러면 위와 같이 각 요리의 순서에 대해 어떤 그룹에 그 요리가 들어가게 할지 결정할 수 있지 않을까요? 이를 위하여 다음과 같은 DP식을 정의해봅시다.
\(dp[i] [j] [k]\): $i$번째 요리까지 총 $j$개의 그룹이 쓰였고, $i$번째 요리가 포함된 구간은 (X or Y)인 경우 최솟값
$k=0$인 경우 현재 그룹을 X라 정의하고, $k=1$인 경우 현재 그룹을 Y라 정의합시다.
그러면 다음 그룹을 어떤 식으로 정의할 수 있을까요?
- $i$번째 요리가 X인 경우
- 이전 까지 그룹이 X이며, 현재 그룹을 X로 두고 싶은 경우 추가적으로 드는 힘은 없습니다. 따라서 $dp[i] [j] [0] = dp[i-1] [j] [0]$입니다.
- 이전 그룹이 X였으며, 현재 그룹을 Y로 두고 싶은 경우는 항상 답보다 큰 값이 나오기 때문에 고려하지 않아도 됩니다.
- 이전 그룹이 Y였으며, 현재 그룹을 X로 두고싶은 경우 Z하나를 가져와 사이에 두어야 하므로 1만큼의 힘이 듭니다.따라서 $dp[i] [j] [0] = dp[i-1] [j-1] [1] + 1$입니다. 이 때 새로운 그룹을 만들어야 하므로 사용한 그룹의 개수도 1 늘려주어야 합니다.
- 이전 그룹이 Y였으며, 현재 그룹을 Y로 두고싶은 경우 현재 X를 뺀 후 다른 X그룹에 두어야 합니다. 이는 1만큼의 힘이 들기 때문에 $dp[i] [j] [1] = dp[i-1] [j] [1] + 1$입니다.
- $i$번 요리가 Y인 경우, X인 경우와 같으므로 생략하겠습니다.
- $i$번 요리가 Z인 경우
- 이전까지 그룹이 X였으며, 이를 계속 유지하고 싶다면 아무런 힘도 들지 않습니다. 따라서 $dp[i] [j] [0] = dp[i-1] [j] [0]$입니다.
- 이전까지 그룹이 X였으며, 현재 Z를 통해 Y로 전환하고 싶을 때에도 아무런 힘이 들지 않습니다. 따라서 $dp[i] [j] [1] = dp[i-1] [j-1] [0]$입니다.
- 이전 그룹이 Y인 경우는 이전 그룹이 X인 경우와 같으므로 생략하겠습니다.
이런 식으로 DP를 설계해 주면 되는데, 하나의 궁금증이 듭니다. X에서 3번째 경우, 단순히 1만 더해주면 되는 건가요? 어떤 Z를 가져올 지 고려해주지 않아도 되나요?
이에 대한 답은, 고려해주지 않아도 된다는 겁니다. 다음의 그림을 한 번 보겠습니다.
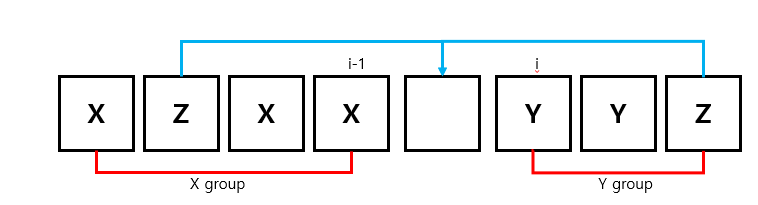
$i-1$번째까지 X그룹이라고 하는 상태에서 i번째 그룹을 Y로 변환한다고 합시다. 이 때 X그룹 혹은 Y그룹 내에는 힘을 들이지 않은 Z가 하나 이상 존재하여야 합니다. 우리가 만들 수 있는 그룹이 최대 K개이며, 만약 K개 이내로 그룹을 만들었고 그 사이에 Z가 들어있지 않은 경우가 존재한다면 그 Z는 X나 Y그룹 내에 존재할 수 밖에 없습니다. 따라서 Z를 고려할 때 어떤 그룹내에 속해있었을 때 힘을 추가하지 않고, 새로운 그룹을 생성할 때 기존 어떤 그룹안에 속해 있던 Z를 뺀 후 이 사이에 추가해준다고 생각하면 됩니다.
이후, 우리는 총 K개의 그룹을 만들 수 있고, X가 속한그룹과 Y가 속한 그룹 모두 하나 이상 존재해야 하므로
$Answer = min_{2 \leq j \leq K}(dp[N] [j] [0], dp[N] [j] [1])$이 정답이 됩니다.
코드
#include <bits/stdc++.h>
using namespace std;
int n,m,X[2],arr[5001],dp[5001][5001][2];
int DP(int idx,int rem,int pre) {
if(idx == n) return rem==0 ? 0 : n+1;
int &ret = dp[idx][rem][pre];
if(ret!=-1) return ret;
ret = n+1;
int f = 2;
if(arr[idx] == X[0]) f = 0;
else if(arr[idx] == X[1]) f = 1;
// Change Segs
if(rem) {
if(f==2) ret = min(ret, DP(idx+1, rem-1, pre^1));
else if(pre == f) ret = min(ret, DP(idx+1, rem-1, pre^1) + 2);
else ret = min(ret, DP(idx+1, rem-1, pre^1) + 1);
}
// Step
if(f==2 || f==pre) ret = min(ret, DP(idx+1, rem, pre));
else ret = min(ret, DP(idx+1, rem, pre)+1);
return ret;
}
int main() {
scanf("%d%d%d",&n,&X[0],&X[1]);
for(int i=0;i<n;i++) scanf("%d",arr+i);
int cnt = 0, t1=0, t2=0;
for(int i=0;i<n;i++) {
if(arr[i] != X[0] && arr[i] != X[1]) cnt++;
else if(arr[i] == X[0]) t1++;
else t2++;
}
if(t1 && t2 && !cnt) puts("-1");
else if(!t1 || !t2) puts("0");
else {
memset(dp,-1,sizeof(dp));
int ans = n;
for(int i=2;i<=cnt+1;i++) ans = min(ans, min(DP(0,i-1,0), DP(0,i-1,1)));
printf("%d\n",ans);
}
return 0;
}
Eulerian Flight Tour (Yokohama 2018)
어떤 양방향 그래프에서 Eulerian tour를 할 수 있다는 것을 다음과 같이 정의합니다.
- 경로의 시작점과 끝점이 같아야 합니다.
- 모든 정점을 최소 한 번 이상 들려야 합니다.
- 모든 간선을 단 한 번만 사용해야 합니다.
어떤 양방향 그래프가 주어지면 Eulerian tour를 할 수도 있고, 그렇지 못할 수도 있습니다. 모두 만족한다면 좋겠지만, 그렇지 않은 경우 우리는 다음의 조건을 지키며 새로운 간선을 추가할 수 있습니다.
- 어떠한 정점 $u, v$사이에는 최대 한 개의 간선만 있어야 합니다.
그래프가 주어지면, Eulerian tour를 할 수 있는 그래프를 만들 수 있는지 확인하고, 가능하다면 그 그래프를 만들기 위해서 추가해주어야 하는 간선들을 찾아주세요.
문제에서 정점의 개수를 $N$개, 간선의 개수를 $M$개라 하면 주어지는 인풋의 범위는 $3\leq N \leq 100$, $0\leq M \leq \frac{N(N-1)}{2}입니다.
풀이
제목 “Eulerian”이라는 단어와, 문제에서 “Eulerian Circuit”이라는 알고리즘을 떠올릴 수 있습니다. 우선, Eulerian Circuit문제가 어떤 것인지 다시 확인해보도록 합시다.
- Eulerian Circuit: 임의의 연결 그래프하나가 주어질 때 모든 간선을 무조건 한 번 방문하고, 시작점으로 돌아오는 경로
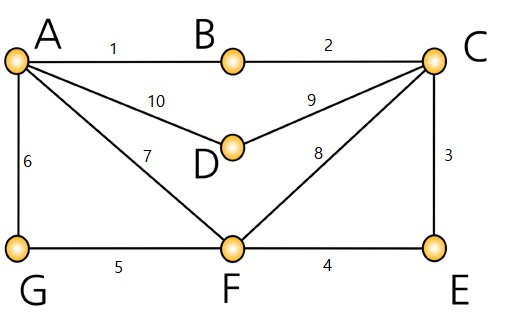
위의 그래프에서 정점 A에서 번호 순서대로 이동을 하면, 모든 간선을 한 번 방문하고 A정점으로 돌아올 수 있습니다.
이와 비슷한 문제인 것 같은데, 이 Eulerian Circuit을 찾을 수 있는 방법이 있을까요? 다행히도, 어떤 연결 그래프에서 Eulerian Circuit을 만들 수 있는지 확인하는 방법이 존재합니다.
- 정점 $v$에 대해, $v$와 연결된 간선의 개수를 $d_v$라 합시다. 이 때 모든 정점 $v$에 대해 $d_v$가 짝수라면 항상 Eulerian Circuit을 만들 수 있습니다.
즉, 모든 정점의 차수가 짝수라면 Eulerian Circuit을 만들 수 있습니다. 그러면, 문제에서 주어진 그래프가 Eulerian Circuit을 만족하도록 하려면 차수가 홀수인 정점들끼리 간선을 추가해주어야 될 것입니다.
그러면 간선은 어떤 식으로 추가할 수 있을까요? 차수가 홀수인 정점사이에만 간선을 추가한다고 할 수 있지만, 주어진 그래프에서 그 두 정점 사이에 이미 간선이 존재한다면 간선을 추가할 수 없을 것입니다. 그렇기에, 양 정점 사이에 간선을 하나만 추가한다고 생각하지 말고, 두 경로를 잇는 경로를 하나 추가해준다고 생각해봅시다.
우리가 어떤 경로 $u_1, u_2, …, u_n$을 추가한다고 할 때 각 정점의 차수는 어떤 식으로 바뀔까요? $u_1, u_n$정점은 하나의 간선만 추가되니 홀수였다면 짝수, 짝수였다면 홀수가 됩니다. 반면 $u_1, u_n$을 제외한 나머지 정점들은 간선이 2개 추가되기 때문에 홀수, 짝수가 유지됩니다.
따라서 우리는 차수가 홀수인 정점쌍들 사이에 임의의 경로를 추가할 수 있다면 Eulerian Circuit을 만족하게 만들 수 있습니다. 그럼 어떤식으로 이런 경로를 추가해야 될까요?
우리가 새로운 간선을 추가해야 되기 때문에, 입력으로 주어진 그래프에서 없는 간선들로 새로운 그래프를 만들어봅시다. 그리고 새로 만든 그래프에서 아무 트리나 하나 그려줍시다.
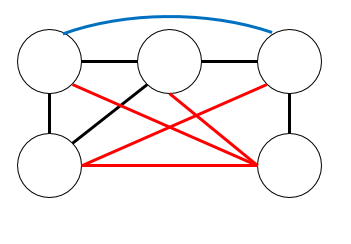
위의 그림에서, 검은색 간선은 입력으로 주어진 간선, 빨강 & 파랑 간선은 이를 제외한 간선이며 그 중 빨강 간선은 새로운 그래프에서 만든 임의의 트리입니다.
그 트리에서 보았을 때, 이 트리상의 모든 정점의 차수가 짝수가 될 수 있도록 만들 수 있다면, 홀수 차수를 가진 정점의 개수가 짝수개여야 하고, 아니라면 만들 수 없습니다. 아닐 경우를 먼저 생각해볼 때, 어떤 정점의 차수를 짝수로 만드려면 다른 홀수차수를 가진 정점과 이어지는 경로를 만들어야 하지만, 자신에서 갈 수 있는 모든 홀수정점은 이미 다른 홀수정점과 이어진 상태일 것이기 때문에 그 정점의 차수를 짝수로 만들 수 없습니다. 만약 차수가 홀수인 정점이 짝수개라면 임의의 정점을 트리의 루트로 잡은 다음 그 정점의 서브트리에 있는 홀수정점의 개수가 홀수개라면, 그 정점과 부모를 잇는 간선을 추가해 주는 방식으로 만들 수 있습니다.
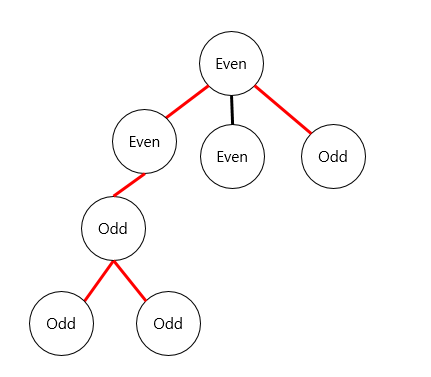
위 그림에서, 빨간 간선이 추가해주어야 할 간선입니다.
이렇게 만든 다음, 아까 우리가 고려하지 않은 조건을 하나 해결해야 합니다.
- 모든 정점을 한 번 이상 방문하여야 한다.
Euler Circuit을 찾으면 자연스럽게 해결될 문제이지만, 모든 정점이 연결되있다는 가정이 없으므로 이 조건을 아직 해결하진 못합니다.
이를 해결하기 위해, 위에서 기술한대로 추가간 간선들과 인풋에서 주어진 간선들로 만든 새로운 그래프를 하나 생각해봅시다. 이들을 연결그래프로 만들기 위해서는 다음과 같은 과정을 거치면 됩니다.
-
만약 컴포넌트가 3개 이상일 경우, 각 컴포넌트에서 정점을 하나씩 골라 이를 잇는 사이클을 하나 만들어줍니다.
-
만약 컴포넌트가 1개일 경우, 이미 하나의 연결그래프이므로 굳이 간선을 추가해주지 않아도 됩니다.
-
만약 컴포넌트가 2개이고 각 컴포넌트의 정점의 개수가 모두 2개 이상이라면 각 컴포넌트에서 정점을 2개씩 골라 이를 이어주면 됩니다.
-
만약 컴포넌트가 2개이고 정점개수가 1개인 컴포넌트가 있다면, 다음 과정을 거쳐줍시다.
- 다른 컴포넌트의 정점 2개를 골라 이 둘 사이에 간선이 없다면 그 두 정점과 다른 컴포넌트의 정점을 연결해줍니다.
- 이 둘 사이에 새로 추가된간선이 있다면, 새로 추가된 간선을 지우고 두 정점과 다른 컴포넌트의 정점을 연결해줍니다.
- 만약 두 경우 모두에 해당이 안된다면, 그 그래프는 Eulerian tour를 할 수 있도록 만들 수 없습니다.
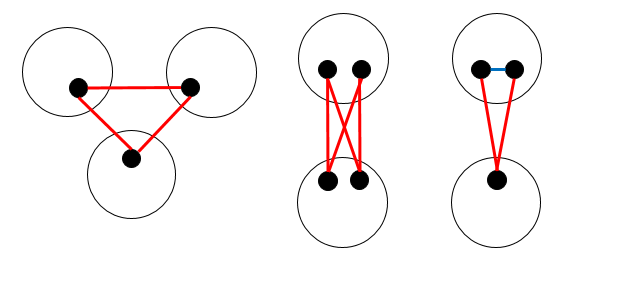
위에서 기술한대로 간선을 추가하는 방법이며, 가장 오른쪽에서 파란 간선에 대해서는 추가된 간선이라면 파란 간선을 지우고, 아니라면 파란 간선을 추가하여야 합니다.
위와같이 간선을 모두 추가해주면 원하는 답을 찾을 수 있습니다.
코드
#include <bits/stdc++.h>
#define fi first
#define se second
using namespace std;
using pii = pair<int,int>;
int n,m,adj[101][101],nadj[101][101];
vector<pii> ans;
int vis[101],deg[101],pa[101],sz[101];
void addEdge(int u,int v) {
if(u>v) swap(u,v);
nadj[u][v] = nadj[v][u] = 1;
adj[u][v] = adj[v][u] = 1;
}
int dfs(int cur) {
vis[cur]=1;
int s=deg[cur]%2;
for(int i=1;i<=n;i++) if(!vis[i] && !adj[cur][i]) {
int cand = dfs(i);
s+=cand;
if(cand) addEdge(cur, i);
}
return s%2;
}
int find(int cur) {
return cur==pa[cur] ? cur : pa[cur] = find(pa[cur]);
}
void merge(int u,int v) {
u=find(u); v=find(v);
if(u!=v) {
pa[v] = u;
sz[u] += sz[v];
}
}
int main() {
scanf("%d%d",&n,&m);
for(int i=0,u,v;i<m;i++) {
scanf("%d%d",&u,&v);
adj[u][v] = adj[v][u] = 1;
deg[u]++;deg[v]++;
}
for(int i=1;i<=n;i++) if(!vis[i]) {
int cand = dfs(i);
if(cand) {
puts("-1");
return 0;
}
}
for(int i=1;i<=n;i++) pa[i] = i,sz[i] = 1;
for(int i=1;i<=n;i++) {
for(int j=1;j<=n;j++) if(i!=j && adj[i][j]) merge(i,j);
}
int cs = 0;
vector<int> ga;
for(int i=1;i<=n;i++) if(find(i)==i) {
cs++;
ga.push_back(i);
}
if(cs==2) {
if(sz[ga[1]]==1) swap(ga[0],ga[1]);
if(sz[ga[0]]==1) {
int f=0;
for(int i=1;i<=n && !f;i++) for(int j=1;j<=n && !f;j++) if(i!=j && i!=ga[0]&&j!=ga[0]) {
if(!adj[i][j]) {
addEdge(i, ga[0]);
addEdge(j, ga[0]);
addEdge(i, j);
f=1;
break;
} else if(nadj[i][j]) {
addEdge(i,ga[0]);
addEdge(j,ga[0]);
nadj[i][j] = nadj[j][i] = 0;
adj[i][j] = adj[j][i] = 0;
f=1;
break;
}
}
if(!f) {
puts("-1");
return 0;
}
} else {
int gc[2] = {0, 0};
for(int i=1;i<=n;i++) for(int j=0;j<2;j++) if(i!=ga[j] && find(i)==ga[j]) {
gc[j] = i;
}
addEdge(ga[0], ga[1]); addEdge(ga[0],gc[1]);
addEdge(ga[1], gc[0]); addEdge(gc[0],gc[1]);
}
} else if(cs>2) {
for(int i=0;i<cs;i++) {
addEdge(ga[i],ga[(i+1)%cs]);
}
}
for(int i=1;i<=n;i++) for(int j=i+1;j<=n;j++) if(nadj[i][j]) {
ans.push_back({i,j});
}
printf("%lu\n",ans.size());
for(auto &it:ans) printf("%d %d\n",it.fi,it.se);
return 0;
}