2019 SCPC Round 2 5번 풀이
문제 요약
$M \times M$ 격자판에 $N$ 개의 점이 찍혀 있다. 각 점에 대해서, 그 점은 왼쪽 아래로 하는 가장 큰 정사각형을 그리려 한다. 단, 정사각형은 $N$ 개의 점중 어떤 점이라도 내부에 포함시키면 안된다.
모든 점에 대해서 정사각형을 그릴 때, 모든 정사각형 변의 합을 구하시오.
$2 \le M \le 10^9$, $1 \le N \le 500000$
풀이
1.
먼저 2D Range Tree 를 써서 특정 직사각형 구간에 점의 개수를 $O(\log^2 N)$ 시간에 알 수 있다. 여기에 이분탐색을 더하면 $O(N \log^2 N \log M )$ 으로 해결 할 수 있다.
2.
위와 비슷하지만 2D Range Tree 를 쓰지 않고 Persistent Segment Tree 를 사용한다. 그러면 특정 직사각형 구간에 점의 개수를 $O(\log N)$ 시간에 알 수 있다. 여기에 이분탐색을 더하면 $O(N \log N \log M )$ 으로 해결 할 수 있다.
위 두 풀이는 시간초과가 난다.
3.
아이디어를 소개한다. 문제를 정사각형을 찾는 것이 아니라, 직각삼각형을 찾는 방식으로 방향을 돌린다. 정확히는 각 점에 대해서, 그 점을 왼쪽 아래로 하며 45도 각을 가지게 하는 최대 직각삼각형을 구하는 것이다.
아래 그림은 위의 아이디어를 설명한다.
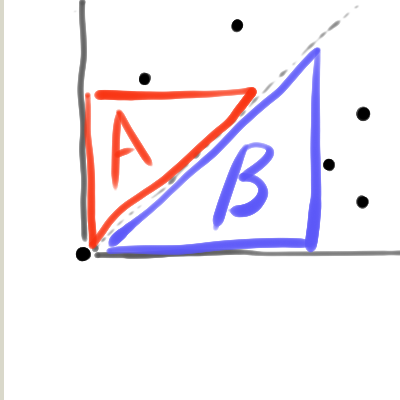
모든 점에 대해서 A 타입의 최대 직각이등변삼각형을 구할 수 있다면, $(x, y)$ 점을 $(y, x)$ 으로 바꾸고 같은 방법을 진행하면 B 타입의 최대 직각이등변삼각형도 구할 수 있다. 따라서, 모든 점에 대해서 최대 A 타입 직각이등변삼각형을 구하는 문제로 바뀐다.
자료구조를 하나 준비하자, 점 갱신, 구간 최솟값 쿼리가 $O(\log N)$ 가능하면 모든 가능하다.
각각의 점을 $(x, y)$ 에 대해서 자료구조의 key 값을 $y-x$ 로 하고, value 값을 $y$ 로 하자.
모든 준비가 끝났다. 주어진 $N$ 개의 점들을 x 기준 내림차순, x 가 같다면 y 기준 오름차순으로 정렬한다. 정렬한 순서 대로 순회를 하자. 현재 순회하고 있는 점을 $(x, y)$ 라 하자. 자료구조에서 $[y-x, \inf]$ 에 구간 최솟값 쿼리를 요청한다. 요청해서 얻은 값을 $p$라고 하면, 이 점에 대해 직각이등변삼각형의 이등변의 길이는 $p-y$이다. (만약 점이 없었다면, $M-y$ 로 처리하면 된다.)
각 순회마다 $O(\log N)$ 이므로, 총 시간복잡도는 $O(N \log N)$이다.
코드
#include <bits/stdc++.h>
using namespace std;
#define SZ(v) ((int)(v).size())
#define ALL(v) (v).begin(),(v).end()
#define one first
#define two second
using ll = long long;
using pi = pair<int, int>;
using ti = tuple<int, int, int>;
const int INF = 0x3f3f3f3f;
const ll LINF = 1ll * INF * INF;
int getL(int k, vector<int> &v) {
return lower_bound(ALL(v), k) - v.begin();
}
int getU(int k, vector<int> &v) {
return upper_bound(ALL(v), k) - v.begin();
}
struct IDX {
int P; vector<int> val;
IDX(int N) {
for(P=1; P<N; P<<=1);
val = vector<int>(P*2, INF);
}
void update(int v, int k) {
val[v+=P] = k;
while(v>>=1) val[v] = min(val[v*2], val[v*2+1]);
}
int getMin(int a, int b) {
int res = INF;
for(a+=P, b+=P; a<=b; a>>=1, b>>=1) {
if(a%2==1) res = min(res, val[a++]);
if(b%2==0) res = min(res, val[b--]);
}
return res;
}
};
const int MAX_N = 5e5 + 10;
int N, L;
ti Nr[MAX_N];
int Ans[2][MAX_N];
void getLength(vector<ti> nr, int tp) {
vector<int> As, Bs;
for(int i=0; i<N; i++) {
int x, y, ix; tie(x, y, ix) = nr[i];
int a = y - x;
As.push_back(a);
}
sort(ALL(As)); As.erase(unique(ALL(As)), As.end());
IDX idx = IDX(SZ(As));
sort(ALL(nr), [&](ti a, ti b) {
int ax, ay; tie(ax, ay, ignore) = a;
int bx, by; tie(bx, by, ignore) = b;
return pi(-ax, ay) < pi(-bx, by);
});
for(int i=0; i<N; i++) {
int x, y, ix; tie(x, y, ix) = nr[i];
int minL = 1;
int maxL = L - y;
int a = getL(y-x, As);
int minY = idx.getMin(a, SZ(As)-1);
Ans[tp][ix] = min(maxL, minY - y);
idx.update(a, y);
}
}
void solve() {
scanf("%d%d", &L, &N);
vector<ti> nr;
for(int i=0; i<N; i++) {
int x, y;
scanf("%d%d", &x, &y);
nr.emplace_back(x, y, i);
}
getLength(nr, 0);
for(int i=0; i<N; i++) {
int x, y, ix; tie(x, y, ix) = nr[i];
nr[i] = ti(y, x, ix);
}
getLength(nr, 1);
ll ans = 0;
for(int i=0; i<N; i++) {
ans += min(Ans[0][i], Ans[1][i]);
}
printf("%lld\n", ans);
}
int main() {
int TC; cin >> TC;
for(int tc=1; tc<=TC; tc++) {
printf("Case #%d\n", tc);
solve();
}
return 0;
}