번사이드 보조정리(Burnside Lemma)
서론
Burnside Lemma(번사이드 보조정리)는 Group action에서 나오는 정리입니다. 여기서 말하는 Group이란 대수학에서의 Group을 의미합니다. Competitive Programming에서 아주 가끔씩 경우의 수를 세는 문제에서 활용이 되나 객관적으로 나올 확률은 굉장히 낮다고 볼 수 있습니다.
이 글 자체는 Group Theory의 기초부터 차근차근 설명을 할 예정이지만 만약 Group Theory에 대해 이전에 전혀 공부를 한 적이 없다면 안타깝게도 이론적 배경을 이해하는 것이 불가능에 가까울 것입니다. 대신 이론적 배경을 이해하지 않고 하단의 실제 문제에서 Burnside Lemma를 사용하는 예시만을 익혀두어도 괜찮습니다.
배경 지식 1 - Group
Burnside Lemma를 다루기 이전, Group Theory를 먼저 공부하고 가겠습니다. Group Theory는 Group이라는, 어떤 좋은 연산에 대해 닫혀있는 특수한 집합에 대해 여러 성질을 탐구하는 이론입니다. set $G$와 set $G$에서 정의된 closed binary operation *가 아래 3가지 성질을 만족할 때 우리는 $(G, *)$를 Group이라고 부릅니다.
- Associativity(결합 법칙)가 성립합니다.
- Identity(항등원)이 존재합니다. 항등원이 일단 존재한다면 유일함은 쉽게 보일 수 있습니다.
- 모든 원소에 대해 inverse(역원)이 존재합니다. 마찬가지로 역원이 일단 존재한다면 유일함을 쉽게 보일 수 있습니다.
예를 들어 $(\mathbb{R}, +)$는 결합법칙이 성립하고, $0$이라는 항등원이 존재하고, 임의의 원소 $a$에 대해 $-a$라는 역원이 존재하므로 Group입니다. 그러나 $(\mathbb{Z}_+, +)$는 항등원이 존재하지 않고, $(\mathbb{Z}, *)$는 $1, -1$이 아닌 모든 원소에 대해 역원이 없으므로 Group이 아닙니다.
이 글에서 전부 다루지는 않겠지만, 어떤 집합이 Group임으로서 얻게 되는 좋은 성질들이 있습니다. 우리는 성질을 알고 싶은 어떤 집합에 대해, 직접 다양한 성질들을 증명할 필요가 없이 그저 그 집합이 Group임을 증명하기만 하면 Group의 성질들을 가져다 쓸 수 있게 됩니다. 그렇기에 Group이라는 추상적인 개념을 다양한 문제에서 활용할 수 있게 됩니다.
배경 지식 2 - Group Action
Group Action은 Group은 아닌 어떤 집합 $X$의 성질을 Group $G$로부터 유추할 수 있게 해주는 Action입니다. 우선 정의를 살펴봅시다. $X$는 집합이고 $G$는 Group일 때 아래의 성질을 만족하는 map $* : G \times X \rightarrow X $를 action of $G$ on $X$라고 부릅니다.
- 모든 $x \in X$에 대해 $ex = x$입니다.($e$ : $G$의 항등원)
- 모든 $x \in X, g_1, g_2 \in G$에 대해 $(g_1g_2)(x) = g_1(g_2x)$ 입니다.
사실 이 Group Action은 보통 커리큘럼 상에서 Subgroup, Group Homomorphism, Factor Group과 같은 주제들을 배우면서 Group에 대해 충분히 익숙해진 이후에 다루기 때문에 이전에 Group에 대해 접해본 적이 없다면 잘 이해가 가지 않는 것이 당연합니다. 그래도 같이 한 번 예시를 통해 Group Action을 이해해봅시다.
우선 Group $G = {r_{0}, r_{90}, r_{180}, r_{270}}$ 이라고 두겠습니다. 각 원소는 도형을 0도, 90도, 180도, 270도 회전시키는 연산입니다. 이 Group은 마치 ${0,1,2,3}$을 덧셈에 대해 연산하는 것과 동일하고, 쉽게 Group의 성질을 만족함을 알 수 있습니다.
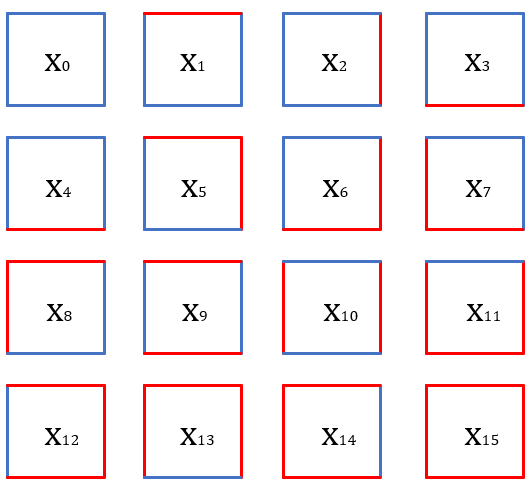
그리고 집합 $X$를 변의 색이 빨강 혹은 파랑이고 변의 길이가 고정된 정사각형의 집합이라고 하겠습니다. $X$의 원소들은 총 16개로, 아래와 같습니다.
이 때 우리는 $X$의 원소를 0, 90, 180, 270도 회전변환 시키는 것으로 Group Action을 정의할 수 있습니다. 예를 들어 $x_1$을 시계 방향으로 90도 회전시킬 경우 $X_2$가 되므로 $r_{90} * x_1 = x_2$입니다. 엄밀하게 증명은 하지 않겠지만, 이 Group Action이 잘 정의됨을 증명할 수 있습니다.
배경 지식 3 - Orbit
Group Action에서 Orbit은 $X$의 partition의 한 종류입니다.(partition은 $X$의 부분집합들의 집합으로, 모든 $X$의 원소는 정확히 한 개의 집합에 속해있습니다. 예를 들어 정수를 짝수와 홀수집합으로 나눈다면 모든 원소는 짝수 혹은 홀수 집합에 속하므로 partition이지만, 정수를 양수와 음수 집합으로 나눈다면 0은 아무 집합에도 속하지 않으므로 partition이 아닙니다.)
이제 Orbit의 정확한 정의를 알아봅시다. $X$의 원소 $x_a, x_b$를 생각해봅시다. 만약 적절한 원소 $g \in G$가 존재해 $x_a = gx_b$로 표현할 수 있다면 $x_a$와 $x_b$는 동일한 Orbit에 속합니다. 참고로 Group Action의 성질에 따라 $x_a = gx_b$이면 $g^{-1}x_a = x_b$이므로 Orbit은 잘 정의되고, 더 나아가 Orbit이 Partition인 것도 증명이 가능합니다.
앞에서 예시로 든 Group Action에서 Orbit은 총 6개로, 아래와 같습니다.
- $x_0$
- $x_1, x_2, x_3, x_4$
- $x_5, x_6, x_7, x_8$
- $x_9, x_{10}$
- $x_{11}, x_{12}, x_{13}, x_{14}$
- $x_{15}$
Burnside Lemma
드디어 번사이드 보조정리를 익히기 위한 배경 지식을 전부 익혔습니다! 이제 번사이드 보조정리에 대해 알아보겠습니다. 번사이드 보조정리는 Group Action에서 Orbit의 갯수를 셀 때 쓰이는 정리입니다.
번사이드 보조정리를 다루기 전, Orbit의 갯수가 어떤 의미를 가지는지를 먼저 알아보겠습니다. 아래와 같은 문제를 생각해봅시다.
변의 색깔이 빨강 혹은 파랑인 서로 다른 정사각형의 갯수는 몇 개인가? 단 회전했을 때 모양이 같은 정사각형은 동일한 정사각형으로 간주한다.
이 문제의 답은 직접 계산해보면 6입니다. 그런데 이 문제의 정답과 위의 Group Action의 관계를 아시겠나요? 위의 Group Action에서 각 Orbit이 회전했을 때 모양이 같은 정사각형들을 묶어놓은 것이므로 Orbit의 갯수가 곧 정답임을 알 수 있습니다.
지금은 16개의 정사각형에 대해서만 고민을 하면 됐으니까 직접 따져보더라도 답을 그럭저럭 쉽게 알 수 있었지만 만약 정이십각형에 대해서 동일한 문제가 주어지면 어떨까요? 답을 구하는 것이 그다지 간단하지 않을 것 같다는 느낌이 옵니다. 이럴 때에는 직접 그림을 그려 계산하는 것 보다 번사이드 보조정리를 이용해 Orbit의 갯수를 세는 것이 간단합니다. 이제 번사이드 보조정리를 알아봅시다.
- 번사이드 보조정리 : $r$을 orbit의 갯수라고 할 때 $r \cdot |G| = \Sigma_{g \in G} |X_g|$ 이다.
위의 식에서 $X_g$는 낯설 것입니다. $X_g = {x \in X | gx = x }$으로, $g$로 연산을 해도 자기 자신으로 그대로 mapping되는 $X$의 원소의 집합을 의미합니다.
위의 Group Action에서 $X_{g_0}, X_{g_90}, X_{g_180}, X_{g_270} $을 알아봅시다.
- 0도 회전하면 모든 $X$의 원소는 모양이 그대로이므로 $X_{g_0} = X$입니다.
- 90도 회전하면 $X$의 원소 중에서 네 변의 색깔이 동일한 $x_{0}, x_{15}$만 모양이 그대로이므로 $X_{g_{90}} = {x_0, x_{15}}$입니다.
- 180도 회전하면 $X$의 원소 중에서 마주보는 변의 색깔이 동일한 $x_{0}, x_{9}, x_{10}, x_{15}$만 모양이 그대로이므로 $X_{g_{180}} = {x_{0}, x_{9}, x_{10}, x_{15}}$입니다.
- 270도 회전하면 $X$의 원소 중에서 네 변의 색깔이 동일한 $x_{0}, x_{15}$만 모양이 그대로이므로 $X_{g_{270}} = {x_0, x_{15}}$입니다.
이제 번사이드 보조정리를 적용하면 $\Sigma_{g \in G} |X_g| = |X_{g_0}|+|X_{g_{90}}|+|X_{g_{180}}|+|X_{g_{270}}|=24$이므로 orbit의 갯수는 $24/4 = 6$임을 알 수 있습니다.
Burnside Lemma의 응용
실제 문제에서 Burnside Lemma가 어떻게 응용되는지 살펴보겠습니다. 백준 온라인 저지에 alex9801님이 만드신 번사이드 보조정리, 포여 열거 정리 문제집이 있습니다.(포여 열거 정리는 번사이드 보조정리의 일반화입니다.) 여기에 모여있는 문제 중에서는 단순히 Burnside Lemma를 사용한다고 끝나는 것이 아니라 전처리 혹은 후처리가 굉장히 복잡한 문제도 섞여 있습니다. 이중에서 그나마 쉬운 문제인 BOJ 6567 - Let it Bead를 가지고 풀이를 해보겠습니다.
이 문제는 구슬의 색의 종류가 $c$개일 때 $s$개의 구슬로 이루어진 서로 다른 목걸이의 갯수가 몇 개인지 묻고 있습니다. 단, 만약 회전하거나 뒤집어서 같은 모양이 나오면 동일한 목걸이로 취급합니다. $X$를 회전이나 뒤집는 경우를 고려하지 않은 모든 목걸이의 집합으로, $G$를 모든 회전과 뒤집는 연산의 group으로 정의합시다. $G$는 뒤집지 않고 회전하는 $c$개의 원소와 뒤집은 후 회전하는 $c$개의 원소가 포함되어 있어 총 $2c$개의 원소로 이루어져 있습니다. 이제 각 $G$의 각 원소에 대해 orbit의 크기를 알아내면 문제를 해결할 수 있습니다.
- 뒤집지 않고 회전하는 원소
목걸이를 $t$만큼 회전했을 때 모양이 그대로인 목걸이는 $gcd(t, s)$를 주기로 동일한 모양이 반복해서 나오는 목걸이임을 알 수 있습니다. 그러므로 $c^{gcd(t,s)}$를 각 $t$에 대해 계산하면 됩니다.
- 뒤집고 회전하는 원소
목걸이의 길이 $s$가 홀수인 경우 하나의 원소는 아무 색이어도 상관이 없고 나머지 원소는 짝을 이루므로 총 $s \cdot c^{(s+1)/2}$ 입니다.
목걸이의 길이 $s$가 짝수인 경우에는 $t$가 홀수, 짝수인 경우를 나눠서 생각해야 합니다. $t$가 홀수이면 모든 원소가 짝을 이루고, $t$가 짝수이면 두 원소는 자기 자신으로 돌아와 짝을 이루지 않고 나머지 원소들은 짝을 이루므로 총 $s/2 \cdot (c^{s/2}+c^{s/2+1})$이 됩니다.
이 모든 경우를 합한 뒤 $|G| = 2s$로 나누면 그것이 곧 서로 다른 목걸이의 갯수가 됩니다. 코드는 아래와 같습니다.
#include <bits/stdc++.h>
using namespace std;
int POW(int a, int b) {
int ret = 1;
for (; b; b >>= 1, a = (a * a))
if (b & 1) ret = (ret * a);
return ret;
}
int main(void) {
while(true){
int c,s;
cin >> c >> s;
if(c==0) break;
int tot = 0;
// 1. 뒤집지 않고 회전만 하는 경우
for(int i = 1; i <= s; i++){
tot += POW(c,__gcd(i,s));
}
// 2. 뒤집은 후 회전하는 경우
if(s % 2 == 0){
tot += s*(POW(c,s/2)+POW(c,s/2+1))/2;
}
else{
tot += s*(POW(c,s/2+1));
}
cout << tot / (2*s) << '\n';
}
}
이 문제가 너무 쉽나요? 그렇다면 august14님이 제 4회 kriiicon에 출제하신 팔찌 문제를 추천드립니다. 식 자체는 똑같은데 적절한 후처리를 통해 시간복잡도를 합리적으로 만들어야 합니다.
맺음말
이번 게시글에서는 번사이드 보조정리에 대해 다뤄보았습니다. 이번 학기에 대수학을 수강하고 있는데 번사이드 보조정리가 등장해서 반가운 마음에 이 글을 작성하게 되었네요. 이 글을 읽으신 분들이 번사이드 보조정리를 이용해서 경우의 수를 세는 문제를 겁내지 않고 풀어낼 수 있으면 좋겠습니다.