June 16, 2019 15:00

서론

다항식 다중계산(Multipoint evaluation)은, $N$차 다항식 $f$에 대해, $Q$개의 원소 $x_1, x_2, \cdots, x_Q$ 를 $O(\max(N, Q)\log^2 \max(N, Q))$ 시간에 계산할 수 있도록 도와주는 도구이다. 이 Multipoint evaluation의 계산을 위해서는, 다항식의 빠른 곱셈, 다항식의 빠른 나눗셈을 알아야 한다.

이 글에서는 이를 계산 하는 빠른 방법을 알아본다.

다항식 곱셈

다항식의 빠른 곱셈에는 FFT를 사용한다. FFT란, $x_0, x_1, \cdots, x_{N=1}$ 을 $X_0, X_1, \cdots, X_{N=1}$으로 다음과 같은 규칙에 따라 바꾸는 변환이다.

$X_k = \sum_{n=0}^{N-1} x_n \omega^{nk} \qquad k = 0,\ldots,N-1, w^N=1 $

이것을 좀 더 풀어서 써보면, 우리는 다항식 $f(a) = x_0 a^0 + x_1 a^1 + \cdots + x_{N-1} a^{N-1}$에 대해서 $a$ 에 $\omega^0, \omega^1, \cdots, \omega^{N-1}$ 을 대입한 값을 얻으려고 하는 것이고, 이것이 FFT의 기초이다.

어떤 다항식을 표현할 때, $f$의 각 항을 표현할 수도 있지만, $f(\omega^0), f(\omega^1), \cdots, f(\omega^{N-1})$ 의 값을 들고 다니는 것으로 다항식을 표현할 수도 있다. 이것이 유일하게 결정되고 이것을 Lagrange Interpolation 이라고 한다.

그러면 이 FFT라는 변환이 만약에 구현 되었다고 할 때, 두 다항식의 곱을 어떻게 구할까?

두 $N-1$차 다항식 $f$와 $M-1$차 다항식 $g$ 가 있을 때, 이 둘을 곱함으로서 얻을 수 있는 다항식은 $ h(x) \equiv f(x)g(x)$는 $N+M-1$차 다항식이다. 여기서, 우리가 $N+M$개 이상의 함수값을 알고 있으면 이 다항식 $h$를 유일하게 결정할 수 있는 것이다. 정해진 수 $a$에 대해, $f(a)$ 와 $g(a)$를 알고 있을 때, $h(a)$를 구하는 것은 어렵지 않으므로,

그래서 $f$와 $g$를 적당히 덧대어서 $N+M$차 다항식을 만든 후, $N+M$ 개의 $f(a)$와 $g(a)$의 값을 구하고, $N+M$개의 $h(a)$의 값을 구한 이후에, 원래 다항식으로 표현 해주면 (inverse FFT, $\omega \rightarrow \omega^{-1}$ 로 변환 해 준 후, 길이로 나누어지면 FFT와 동일한 방식으로 구할 수 있다.) 우리는 두 다항식의 곱을 FFT 3번으로 구할 수 있다.

이제, 우리는 임의의 다항식이 가지는 간단한 성질을 알아보려고 한다. $N$ 을 편의상 짝수라고 가정하자.

$f(a) = x_0 a^0 + x_1 a^1 + \cdots + x_{N-1} a^{N-1}$ 일 때, 이를 홀수와 짝수로 나눈다면,

$E(a) = x_0 a^0 + x_2 a^1 + \cdots + x_{N-2} a^{N/2-1}$

$O(a) = x_1 a^0 + x_3 a^1 + \cdots + x_{N-1} a^{N/2-1}$

그리고, $f(a) = E(a^2) + aO(a^2)$ 으로 표현이 될 것이다. 우리는 어떤 $N-1$차 다항식을 $N/2-1$차 다항식 두개의 합 꼴로 바꾸었다. 이 때, $E(a)$ 와 $O(a)$의 푸리에 변환을 구할 수 있으면, 우리는 $A(\omega^j) = E(\omega^{2j}) + \omega^j O(\omega^{2j})$ 라는 식을 이용해서, $f(a)$의 푸리에 변환을 구할 수 있을 것이다. ($f$는 $\omega^N = 1$, $O, E$는 $\omega^{N/2} = 1$인 $\omega$를 쓰므로, $f$의 푸리에변환을 구할 때 사용 한 $\omega$의 제곱은, $O$와 $E$의 푸리에 변환을 구할 때 사용 한 $\omega$ 이다.)

그래서, 푸리에 변환을 구할 때, 크기가 절반인 원소 2개의 푸리에 변환을 계산 해 주고 합쳐주면 된다. 시간 복잡도는 $T(N) = 2T(N/2) + O(N)$이고, Master’s theorem에 의해서 $T(N) = O(N \log N)$ 이 된다.

이는 다음과 같은 의사 코드로 표현된다. exp(2*pi/N) 은 $\omega$와 동일하다. (python과 유사한 형식을 따랐다)

function FFT(N, [x(0), x(1), ..., x(N-1)]) as return [X(0), X(1), ..., X(N-1)]
  if N = 1: return [x(0)] endif
  [X(0), X(1), ... , X(N/2-1)] = FFT(N/2, [x(0), x(2), ..., x(N-2)])
  [X(N/2), X(N/2+1), ... , X(N-1)] = FFT(N/2, [x(1), x(3), ..., x(N-1)])
  for k from 0 to N/2-1, inclusive:
    change at once:
      X(k) = X(k) + exp(2*pi/N*k*i) X(k+N/2)
      X(k+N/2) = X(k) - exp(2*pi/N*k&i) X(k+N/2)

다항식 나눗셈

어떤 두 다항식 $u$와 $v$가 있다고 하자. $u$를 $v$로 나눈 몫은 $q$, 나머지를 $r$이라고 할 때, 일반적으로 나눗셈이라 함은, $u(x) = q(x)v(x) + r(x)$ 를 만족하는 것이다. 우리는 $(q, r)$을 유일하게 만들기 위해서 $r$의 차수가 $v$의 차수보다 낮은 것을 나머지라고 정의한다.

우리는 여기서, $q(x) = \left\lfloor \dfrac{u(x)}{v(x)} \right\rfloor $ 라고 정의할 것이다. 마치 정수 나눗셈을 표시할 때와 같다.

여기서, 우선 그냥 $\dfrac{u(x)}{v(x)}$ 를 계산 해 보자.

$\dfrac{u(x)}{v(x)} = \dfrac{u_mx^m + \cdots + u_1x^1 + u_0 x^0 }{v_nx^n + \cdots +v_1x^1 + v_0x^0}$

$ = \left(\dfrac{u_m}{x^0} + \dfrac{u_{m-1}}{x^1} + \cdots + \dfrac{u_0}{x^m}\right)\left(\dfrac{x^m}{v_nx^n + \cdots +v_1x^1 + v_0x^0}\right)$

$= \left(\dfrac{u_m}{x^0} + \dfrac{u_{m-1}}{x^1} + \cdots + \dfrac{u_0}{x^m}\right)\left(s(x)+\dfrac{t(x)}{v_nx^n + \cdots +v_1x^1 + v_0x^0}\right) $

여기서, $s(x)$ 와 $t(x)$ 는 $x^m$ 을 $v(x)$ 로 나눈 몫과 나머지 이다.

$s(x)$ 와 $\dfrac{u(x)}{x^m}$의 곱 중, 0차 이상인 것만 남기면, $q(x)$를 구할 수 있을 것이다. $\dfrac{u(x)}{x^m}$은 최고 차항의 계수가 0차이고, $t(x)$는 $n$ 차 보다 작기 때문에, $\dfrac{t(x)}{v(x)}$는 -1차 이하 다항식이다. 즉, 이 둘을 곱한 결과는 -1차 이하이고, 버려지는 부분이다.

그래서 우리는 이 $s$와 $t$를 빨리 구할 수 있으면 된다. 여기서 역시 $k$를 $2^N$꼴이라고 가정하고, $p$를 $k-1$차 다항식이라고 할 때, 다음의 루틴이 $\left\lfloor \dfrac{x^{2k-2}}{p(x)}\right\rfloor$ 를 빨리 구하는 데에 도움을 준다. ($k = 1$ 일때는 $\dfrac{1}{p}$이다.):

$p(x) = p_1(x)x^{k/2} +p_2(x)$ 의 두 $k/2$차 다항식으로 나누자.

$q(x) = \left\lfloor \dfrac{x^{k-1}}{p_1(x)}\right\rfloor$ 라고 하고 (재귀호출로 구할 수 있다), $r(x) = 2q(x)x^{(3/2)k-2} - (q(x))^2 (p_2(x))$이라고 하면,

$\left\lfloor \dfrac{r(x)}{x^{k-2}}\right\rfloor$ 가 $\left\lfloor \dfrac{x^{2k-2}}{p(x)}\right\rfloor$ 와 같다.

증명은, $r(x)p(x)$와 $x^{3k-4}$의 차이가 최대 $2k-3$차 다항식이라는 것으로 보일 수 있다:

처음에 구한 몫에 대해, $qp_1 = x^{k-2}+ t(x)$ 라고 하면,

$rp = 2q p_1 x^{2k-2} +2qp_2 x^{(3/2)k-2} - (qp_1 x^{k/2}+qp_2)^2$

$ = 2(x^{k-2} +t) x^{2k-2} + 2qp_2x^{(3/2)k-2} - ((x^{k-2}+t)x^{k/2}+qp_2)^2$

$=2x^{3k-4} + 2tx^{2k-2}+2qp_2x^{(3/2)k-2}-x^{3k-4}-2x^{(3/2)k-2} ( tx^{k/2}+qp_2)-(tx^{k/2}+qp_2)^2$

$=x^{3k-4} - (tx^{k/2}+qp_2)^2$

이고, 마지막 항은 최대 $2k-4$ 차 다항식으로, 우리가 구한 과정이 올바르다는 것을 보일 수 있다.

여기서, $s$와 $t$ 를 구하는 시간 복잡도는 곱셈의 시간복잡도를 $M(n)$ 이라고 했을 때, $T(n) = T(n/2)+M(n)$이므로 $M(n)$ 이고, 곱셈 한번이 있으므로, 나눗셈의 시간 복잡도는 $M(n)$ 과 동일하다는 것을 알 수 있다.

다중계산

다중계산을 할 때, 우리는 $N-1$ 차 다항식을 $N$ 개의 점에 대해서 구할 것이다. (역시 $N=2^k$ 이다.)우리는 강력한 정리 하나를 이용할 것이다:

$f(x)$를 $(x-a)g(x)$ 로 나눈 나머지를 $r(x)$ 라고 할 때, $f(a)$는 $r(a)$ 와 같다.

증명은, $f(x) = (x-a)g(x)q(x) + r(x)$ 에, $x = a$를 대입하는 것으로 쉽게 보일 수 있다.

그래서, 우리는 점 $a_0, a_1, \cdots, a_{N-1}$에 대해,

$f(x)$를 $(x-a_0)(x-a_1) \cdots (x-a_{N/2-1})$ 로 나눈 나머지를 구하고, 이 다항식에 $a_0, a_1, \cdots, a_{N/2-1}$를 대입한 값을 구하고, $f(x)$를 $(x-a_{N/2})(x-a_{N/2}+1) \cdots (x-a_{N-1})$로 나눈 나머지를 구하고, 이 다항식에 $a_{N/2}, a_{N/2+1}, \cdots, a_{N-1}$를 대입한 값을 구하면 이 두개를 그냥 합쳐주는 것으로 정답을 구할 수 있다.

만약, 우리가 이 다항식을 미리 알고 있으면, 각 단계에서 나눗셈만 하면 되기 때문에 $O(n \log n)$의 시간이 든다.

$T(n) = 2T(n/2) + O(n \log n)$이므로, Master’s theorem에 의해 $T(n) = O(n \log^2 n)$이다.

이 다항식의 값은 어떻게 알 수 있을까?

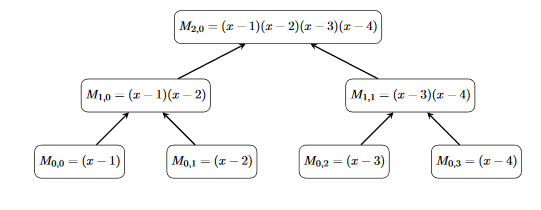
다음과 같은 polynomial tree를 관리 해 주자. 이 Polynomial tree는, 왼쪽 자식과 오른쪽 자식의 곱을 그대로 사용해서 부모의 곱이 되는 것이고, 이 문제에서 그대로 사용할 수 있는 다항식을 제공해 준다. 이 트리를 만드는 데에도, $T(n) = 2T(n/2) + O(n \log n)$이므로, $T(n) = O(n \log^2 n)$의 시간복잡도가 든다.

결론적으로, 우리는 다중계산을 $O(N \log^2N)$ 시간에 할 수 있다.

이용

다중계산은 여러곳에 이용될 수 있다.

예를 들면 $(n^2)! \mod p$ 를 $O(n \log^2 n)$ 시간에 구할 수 있다.

$(x+1)\cdots(x+(n-1))(x+n)$ 을 $x=0, n, 2n, \cdots, (n-1)n$ 에 대해 다중계산을 해서 곱해주면 된다. 이를 이용하여 이항계수 $C(n, r) \mod p$ 를 $p$가 소수일 때 $O(\sqrt{p} \log^2 p)$ 시간 에 구할 수 있다.

이외에도, 먼저 얘기가 된 Lagrange Interpolation의 다항식 해를 찾는것도 Multipoint Evaluation과 같은 방식을 통하여 만들어 줄 수 있다.