클러스터링(군집화) 개요

클러스터링(군집화)

클러스터링(군집화)은 개체들이 주어졌을 때, 개체들을 몇 개의 클러스터(부분 그룹)으로 나누는 과정을 의미합니다. 이렇게 개체들을 그룹으로 나누는 과정을 통해서, 클러스터 내부 멤버들 사이는 서로 가깝거나 비슷하게, 서로 다른 두 클러스터 사이의 멤버 간에는 서로 멀거나 비슷하지 않게 하는 것이 클러스터링의 목표입니다.

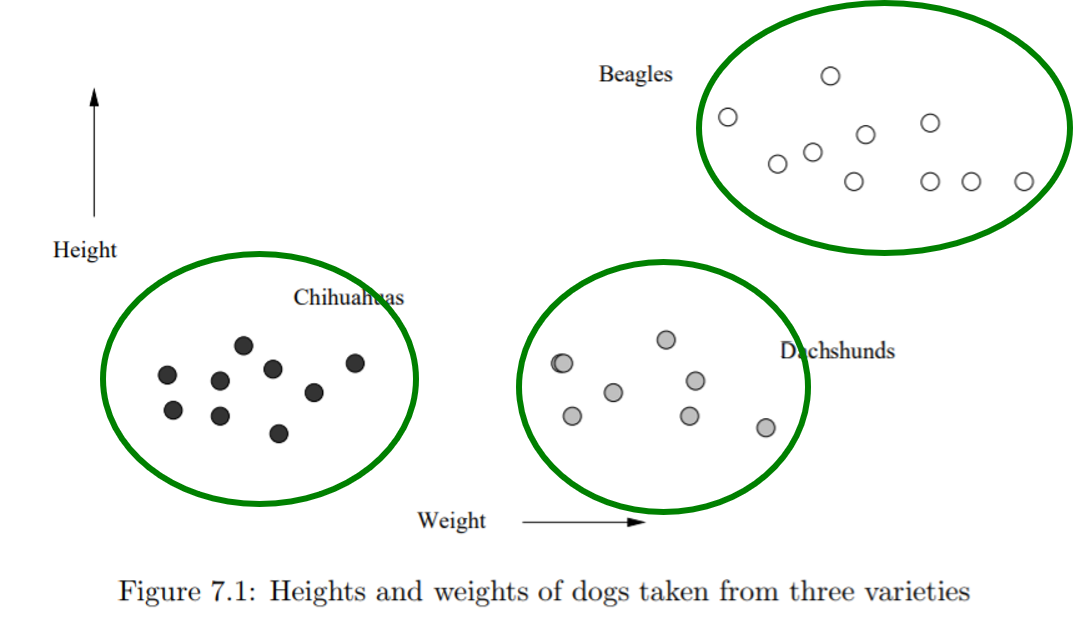
클러스터링의 예시

만약에 개체들을 거리 공간 안에 나타낼 수 있다면, 개체와 개체 사이에 거리(metric)를 정의할 수 있습니다. 예를 들어 개체들을 유클리드 공간 안에 나타낼 수 있다면, 유클리드 거리를 정의할 수 있습니다. 이러한 경우에 클러스터링의 목표는 같은 클러스터 내의 두 멤버들 사이의 거리를 최소화하고, 서로 다른 두 클러스터 사이의 멤버 간의 거리를 최대화하는 것으로 나타낼 수 있습니다.

거리

거리 공간은 공간을 나타내는 집합 $X$와 거리 함수 $d: X \times X \rightarrow [0, \infty)$로 이루어져서, 두 점 사이의 거리가 정의된 공간을 의미합니다. $d$가 거리 함수가 되려면, 아래와 같은 조건들을 만족해야 합니다.

임의의 $x, y \in X$에 대하여, $d(x, y) = 0$과 $x = y$는 동치여야 합니다.
임의의 $x, y \in X$에 대하여, $d(x, y) = d(y, x)$를 만족하여야 합니다.
임의의 $x, y, z \in X$에 대하여, $d(x, y) + d(y, z) \geq d(z, x)$를 만족하여야 합니다. 이 부등식은 주로 삼각부등식으로 잘 알려져 있습니다.

점인 경우에는 유클리드 거리, $L_{p}$ norm 등의 거리를 정의할 수 있고, 집합의 경우에는 자카드 지수 (교집합의 크기 / 합집합의 크기)를, 그리고 문자열의 경우에는 편집 거리나 LCS(최대 부분 공통 문자열)의 길이를 이용하여 거리를 표현할 수 있습니다.

Clustering Algorithms

클러스터링에 사용되는 알고리즘은 크게 계층적 군집(Hierarchical clustering)과 Point assignment clustering 두 가지 방법으로 나눌 수 있습니다.

계층적 군집 방법은 다시 큰 하나의 클러스터로부터 시작해서 모든 클러스터가 정확히 하나의 원소를 가질 때까지 계속 쪼개는 divisive(top-down)한 방법과, 각각의 점을 원소로 가지는 클러스터들로부터 전체를 포함하는 클러스터 하나를 만들 때까지 반복적으로 두 개의 “가까운” 클러스터를 합치면서 진행하는 Agglomerative(bottom-up)한 방법으로 나누어집니다.

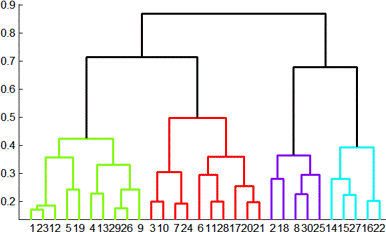
계층적 군집의 예시

Hierarchical Clustering

이 글에서는 Agglomerative한 방법에 대해서만 다룹니다. Agglomerative한 계층적 군집에서 가장 중요한 과정은 바로 반복적으로 두 개의 “가까운” 클러스터를 찾는 것입니다. 거리 공간에서는 거리를 통해서 두 개의 “가까운” 클러스터를 찾을 수 있습니다.

계층적 군집의 알고리즘은 다음과 같이 간단하게 나타낼 수 있습니다.

// V: 클러스터링을 할 set
C: 클러스터를 관리하는 set, 처음에는 비어 있다
for each v in V:
    {v}를 C에 추가한다

while len(C) > 1:
    A, B가 C 안에 있는 가장 가까운 두 클러스터라고 하자
    A, B를 C 안에서 제거하고, A와 B를 합친 클러스터 S를 만든다
    S를 C에 추가한다

두 개의 “가까운” 클러스터를 찾는 방법

거리 공간에서 두 점 사이의 거리를 구하기 위해서는 거리를 구할 두 점이 필요합니다. 그러므로 두 클러스터 안에 원소가 각각 하나만 있다면, 클러스터 사이의 거리를 구하는 것은 어렵지 않을 것입니다. 만약 적어도 한 클러스터 안에 원소가 두 개 이상 존재한다면, 어떻게 거리를 정의할 수 있을까요?

이를 해결하기 위해서, 유클리드 공간에서는 주로 centroid라는 개념을 사용합니다. 대표적으로 centroid를 구하는 방법에는 클러스터 내부에 있는 점의 좌표값의 평균을 이용하는 방법이 있습니다. 예를 들어 클러스터 내에 점이 세 개가 있고, 각각의 좌표가 (0, 0), (1, 2), (2, 1)이라면 centroid의 좌표는 (1, 1)이 됩니다. 이제 유클리드 공간에서는 두 클러스터 사이의 거리는 두 centroid 사이의 거리로 정의할 수 있습니다.

유클리드 공간이 아니라면, centroid가 정의가 되지 않을 수 있다는 문제가 생깁니다. 문자열 “ABCDE”와 “ABEDC”를 생각해봅시다. 이 두 문자열 사이의 편집 거리는 2입니다. (첫 번째 문자열에서 C를 E로 바꾸고, E를 C로 바꾸면 되고, 이보다 더 적은 편집 횟수를 이용하여 두 번째 문자열로 바꾸는 방법은 없습니다.) 그렇다면 이 두 문자열을 원소로 가지는 클러스터의 centroid는 어떻게 정의할 수 있을까요? 먼저 “ABCDE”, “ABEDC”와의 편집 거리가 1인 문자열 “ABCDC”를 생각할 수 있습니다. 그러나 “ABEDE” 또한 원래의 두 문자열과의 편집 거리가 1이 됩니다. 이렇게 비유클리드 공간에서는 centroid를 명확히 정의할 수 없다는 문제가 있습니다.

그래서 비유클리드 공간에서는 centroid 대신에 클러스터 내에서 한 점을 clustroid로 정하게 되고, 두 클러스터 간의 거리를 비교하기 위해서, 두 clustroid 사이의 거리를 이용합니다. 좋은 clustroid를 찾기 위한 방법에는 여러 가지가 있는데, 보통 클러스터 내의 각 점으로부터의 거리들의 최댓값을 최소화하는 점을 선택하거나, 각 점으로부터의 거리들의 평균을 최소화하는 점을 선택합니다.

계층적 군집의 예시

위의 그림은 두 개의 “가까운” 클러스터를 반복적으로 찾는 과정을 표현하고 있습니다. 처음에 (1, 2)와 (2, 1)을 원소를 갖는 클러스터 (파란색 원)를 만들고, centroid를 (1.5, 1.5)로 정합니다. 그 후 (4, 1)과 (5, 0)을 원소로 갖는 클러스터 (녹색 원)을 만들고, centroid를 (4.5, 0.5)로 정합니다. 다음으로 가장 “가까운” 두 개의 클러스터인 (0, 0)을 원소로 가지는 클러스터와 파란색 원 모양의 클러스터를 합쳐서 새로운 클러스터 (왼쪽 빨간색 타원)를 만듭니다. 마지막으로 녹색 원 모양의 클러스터와 (5, 3)을 원소로 가지는 클러스터를 합쳐서 새로운 클러스터(오른쪽 빨간색 타원)을 만듭니다. 마지막으로,남아있는 두 클러스터를 합치면서 계층적 클러스터링의 과정이 끝납니다.

시간 복잡도 분석

시간 복잡도를 분석하기 위해서, 클러스터링을 진행할 집합의 원소의 개수를 $N$이라고 가정합니다. 가장 간단한 방법은 클러스터를 합칠 때마다 매번 두 클러스터 사이의 거리를 모두 계산하는 방법이 있습니다. 그러면 한 번 두 클러스터를 합칠 때마다 $O(N^{2})$의 시간이 소요가 되고, 클러스터를 합치는 횟수가 $N-1$번이기 때문에 시간복잡도가 $O(N^3)$이 됩니다. 이는 비효율적으로, $N$이 $5000$ 정도만 되어도, 매우 오래 걸려서 이 방법을 사용할 수 없습니다.

조금 더 효율적인 방법에는 우선 순위 큐(또는 최대 힙)을 사용하는 방법이 있습니다. 첫 번째 단계에서는 모든 점과 점 사이의 거리를 우선 순위 큐에 넣고, 클러스터를 합칠 때, 클러스터를 합침으로써 영향을 받는 거리들만 다시 계산해주면 됩니다. 처음에 모든 점과 점 사이의 거리를 우선 순위 큐에 넣을 때 $O(N^{2} \log N)$의 시간이 소요되고, 한 번 두 클러스터를 합칠 때 영향을 받는 거리의 수가 $O(N)$이므로, 이 방법의 시간복잡도는 $O(N^{2} \log N)$이 됩니다. 앞에서 다뤘던 비효율적인 방법에 비해서는 훨씬 속도가 개선되었지만, 여전히 $N$의 크기가 커지면 속도가 매우 느려서 사용하기 힘들어진다는 단점이 있습니다.

Point Assignment Clustering

Point Assignment Clustering은 각 cluster가 어떤 개체를 가지는 지 기록하는 방식으로 진행되는 클러스터링 방법입니다. 이 글에서는 간단하면서도 가장 잘 알려진 k-means 알고리즘에 대해서 설명합니다.

K-means Algorithm

k-means 알고리즘은 처음에 클러스터의 개수 $k$를 정하고, 임의로 선택한 $k$개의 점을 이용해 초기의 클러스터 $k$개를 만들고, 클러스터를 계속 알맞게 변화시켜나가면서 클러스터링을 완료하는 방법입니다.

초기에 $k$개의 점을 선택하는 방법으로는 완전히 랜덤하게 $k$개의 점을 선택하는 방법이 쉽게 생각할 수 있는 방법입니다. 또는 처음에 한 점만 랜덤하게 선택하고, 두 번째 점부터는 이전에 선택한 점들로부터 가장 멀리 떨어진 점을 순차적으로 $k-1$개 선택해서 $k$개의 점을 선택하는 방법도 있습니다. 가장 멀리 떨어진 점들을 선택하는 경우, 랜덤하게 선택하는 것보다 점들이 실제로 다른 클러스터에 포함될 가능성이 높다는 장점이 있습니다.

선택한 $k$개의 점을 centroid로 하는 초기의 클러스터 $k$개를 만듭니다. 그리고 전체 점들에 대해서, 각 점마다 가장 가까운 centroid를 찾아서, 찾은 centroid를 기준으로 클러스터를 만듭니다. 이렇게 만들어진 클러스터의 경우, 실제 최적의 centroid가 기존의 centroid와 달라지게 되므로 각 클러스터마다 새로 centroid를 찾습니다. 새로 찾은 centroid를 바탕으로 또 다시 각 점마다 가장 가까운 centroid를 찾아서 클러스터를 만들고, centroid를 다시 조정합니다. 이 과정을 클러스터링한 결과가 달라지지 않을 때까지 반복합니다.

가장 가까운 centroid를 찾는 과정과, centroid를 조정하는 과정에서 유클리드 거리를 사용하게 되므로, 여기서 소개한 k-means 알고리즘은 유클리드 공간에서만 사용 가능합니다.

k-means 알고리즘을 간단하게 표현하면 다음과 같습니다:

초기에 k개의 점을 임의로 선택한다
선택한 점들을 각 클러스터의 centroid로 설정한다
while True:
    for each p in V:
        p로부터 가장 가까운 centroid가 포함된 클러스터에 p를 추가한다
        p를 추가한 클러스터에서 centroid의 좌표를 다시 찾는다
    만약 이전 loop에서 찾은 클러스터 집합과 현재 loop에서 찾은 클러스터 집합이 같다면, 알고리즘을 종료한다

Example

간단한 예시로, 어떠한 직선 위에 있는 점 여덟 개에서 k-means 클러스터링을 해본다고 생각해봅시다. 맨 처음에 $k=2$로 설정하고, 가장 왼쪽에 있는 점과 오른쪽에서 네 번째에 있는 점을 centroid로 선택합니다. 그 후 각 점에서 가장 가까운 centroid를 찾고, 이를 바탕으로 왼쪽 세 점으로 구성된 클러스터와 오른쪽 다섯 개의 점으로 구성된 클러스터를 만듭니다. 그 후 클러스터의 centroid를 다시 정합니다.

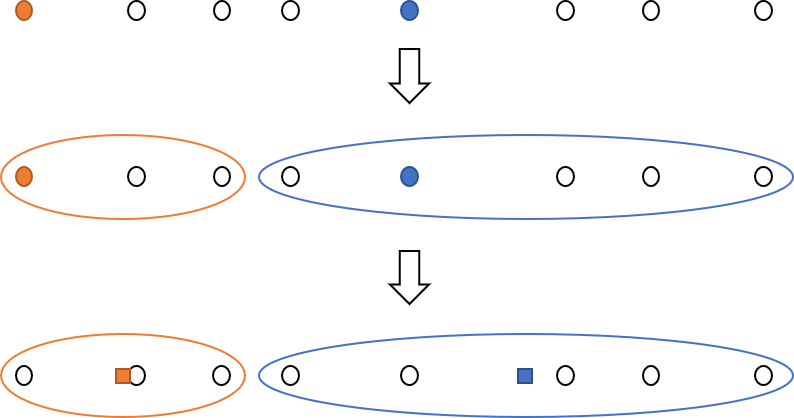
k-means example, step 1

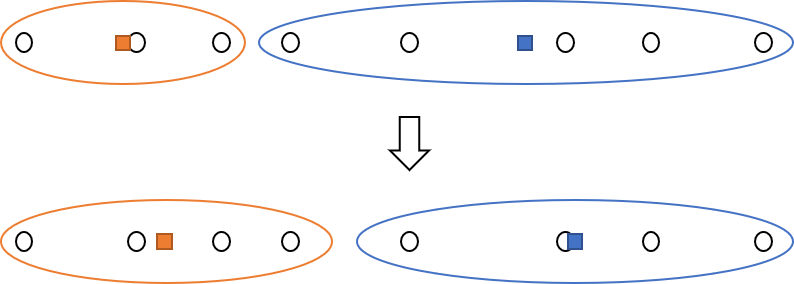
새로 정한 centroid를 이용하여 다시 각 점에서 가장 가까운 centroid를 찾습니다. 이번에는 왼쪽 네 점으로 구성된 클러스터와 오른쪽 네 점으로 구성된 클러스터가 만들어집니다. 다시 centroid의 위치를 조정합니다. 다시 각 점에서 가장 가까운 centroid를 찾아 클러스터를 만들면, 이전에 찾은 클러스터와 변함이 없게 되고, 클러스터링을 종료하게 됩니다.

k-means example, step 2

최적의 k를 찾는 방법

k-means 클러스터링은 처음에 $k$를 선택하고, 클러스터링 과정을 진행합니다. 그러므로 좋은 품질의 클러스터링 결과를 얻기 위해서는 $k$를 잘 선택하는 것이 중요합니다. $k$를 처음에 너무 작게 설정한다면, 실제로는 거리가 멀어서 서로 다른 두 클러스터에 위치해야 하는 점들이 한 클러스터에 묶이게 되는 경우가 생기게 되고, 그 결과 클러스터링의 품질이 떨어지게 됩니다. 반대로 $k$를 처음에 너무 크게 설정한다면 거리가 충분히 가까워서 한 클러스터에 묶일 수 있는 두 점이 다른 클러스터에 속하게 되어서 클러스터링이 비효율적일 수 있습니다.

클러스터링의 품질을 한 클러스터 내의 centroid와 다른 점들 사이의 평균 거리를 이용해서 표현한다고 가정하면, 최적의 k값 근처까지는 평균 거리가 급격히 작아지다가 그 이후부터는 큰 차이가 없는 경향을 보입니다.

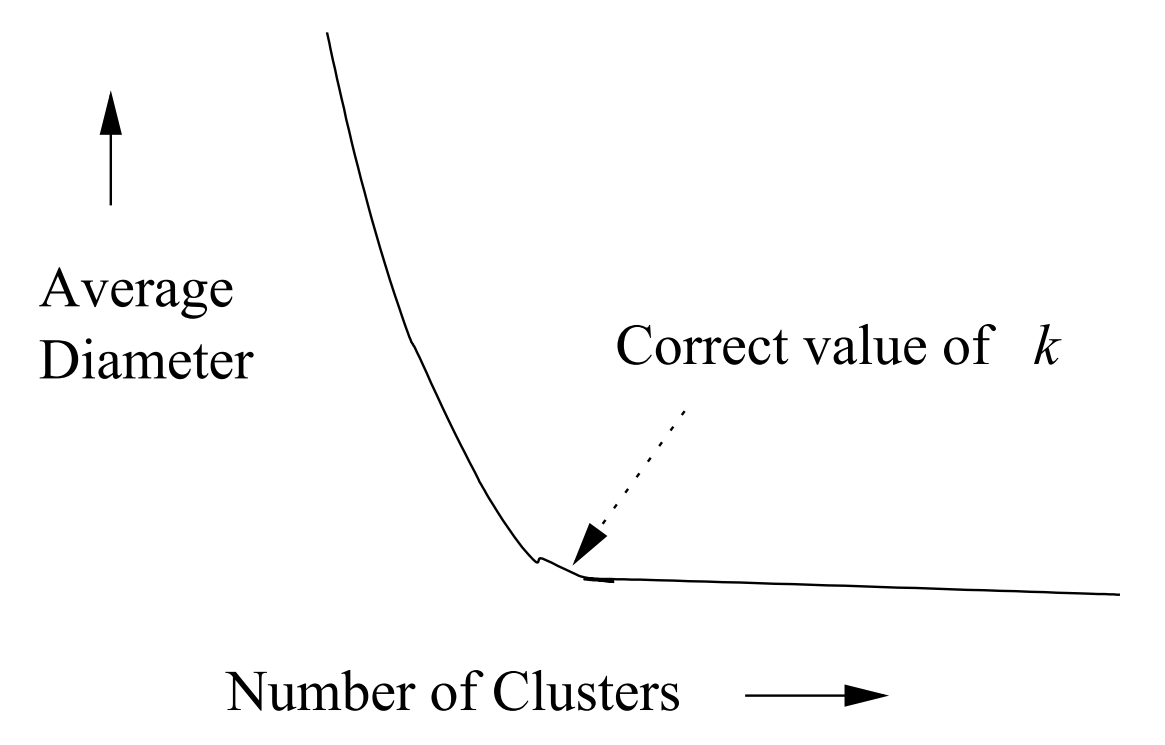
이러한 성질을 사용하여 최적의 $k$를 대략적으로 찾을 수 있습니다. 맨 처음에 k-means 알고리즘을 $k = 1$로 놓고 시도하고, 다음부터는 $k$값을 두 배씩 늘리면서 k-means 알고리즘을 시도합니다. 그렇다면, $k = 2^{i}$와 $k = 2^{i+1}$ 사이에서 평균 거리가 적게 줄어드는 $i$를 찾을 수 있고, 이를 통해 최적의 $k$값은 $2^{i-1}$과 $2^{i}$ 사이에 있다는 사실을 얻을 수 있습니다. 좀 더 정확한 값을 얻고 싶으면 $2^{i-1}$과 $2^{i}$ 사이에서 이분 탐색을 사용하여, 원하는 값을 얻을 수 있습니다. 예를 들어, 현재 최적의 $k$가 $x$ 이상 $y$ 이하의 닫힌 구간에 존재한다는 사실을 안다면, 먼저 $z = (x+y) / 2$로 놓고, $k = z$로 놓고 k-means 클러스터링을 진행합니다. 이 때, $k = z$와 $k = y$ 사이에서 평균 거리가 적게 줄어들었다면, 최적의 $k$는 닫힌 구간 $[x, z]$에 존재한다고 생각할 수 있습니다. 반대의 경우에는 최적의 $k$가 닫힌 구간 $[z, y]$ 에 존재한다고 생각할 수 있습니다.

시간 복잡도

처음에 $k$개의 점을 찾는 것은 $O(k)$의 시간 동안에 수행할 수 있습니다. 그 후, 각 점에서 가장 가까운 centroid를 찾는 과정의 시간 복잡도는 $O(Nk)$이고, centroid를 조정하는 과정의 시간 복잡도는 $O(N)$입니다. 이러한 과정을 $t$번 반복하게 된다면, 전체 시간복잡도는 $O(Nkt)$가 됩니다. $k$값에 따라 $t$가 달라지면서 클러스터링의 수행 시간이 달라지지만, 대체적으로 수행 속도가 빠른 편에 속합니다.

최적의 $k$값을 찾는 과정에서는 처음에 $k$값을 두 배씩 늘리는 횟수가 $O(\log N)$이고, 이분 탐색 과정에서 최대 $O(\log N)$번 탐색하게 되므로, k-means 클러스터링을 $O(\log N)$번 수행하게 됩니다. 그러므로 최적의 $k$값을 찾으면서, k-means 클러스터링을 하는 과정의 전체 시간복잡도는 $O(Nkt log N)$가 됩니다.

문제점

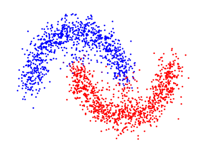
k-means 클러스터링은 유클리드 거리를 사용하기 때문에 클러스터의 모양은 주로 원 형태로 형성됩니다. 만약에 아래 그림과 같이, 최적의 클러스터의 모양이 원 모양이 아닌 경우에는, k-means 클러스터링을 사용하여 최적의 결과를 얻을 수 없습니다. 이러한 문제를 해결한 알고리즘에는 CURE나 DBSCAN과 같은 알고리즘이 있습니다.

k-means 알고리즘으로 좋은 결과를 얻을 수 없는 경우

또한, k-means 알고리즘은 초기에 어떤 점을 선택하는지에 따라 결과가 달라지는 경우가 발생할 수 있다는 문제점을 가지고 있습니다.

마무리

이 포스트에서는 먼저 클러스터링이 어떤 것인지 알아보고, 간단한 클러스터링의 예시로 hierarchical clustering과 k-means clustering에 대해서 자세히 알아보았습니다. 각 알고리즘의 장단점이 존재하므로, 상황에 따라 알맞은 클러스터링 방법을 찾아서 적용하는 것이 좋습니다.

Reference

J. Leskovec, A. Rajaraman, J. Ullman: Mining of Massive Datasets, Chapter 7. Clustering