빠른 다항식 나눗셈

들어가며

두 다항식의 곱셈에는 다양한 방법들이 있습니다. 항을 하나씩 곱해서 더하는 $O(N^2)$ 알고리즘부터, 분할 정복을 이용해 $O(N^{\log_2 3})$의 시간에 동작하는 카라츠바 알고리즘(Karatsuba algorithm), 빠른 푸리에 변환(Fast Fourier transform)을 이용해 $O(N \log N)$의 시간에 동작하는 알고리즘까지 다양합니다.

이 글에서는 다항식의 곱셈을 빠르게 하는 방법을 알고 있다는 것을 전제로, 다항식의 나눗셈을 빠르게 하는 방법을 소개하고, 얼마나 더 빠른지를 비교해 볼 것입니다.

$O(N^2)$ 알고리즘

본격적으로 시작하기 전에, 빠른 다항식 나눗셈 알고리즘이 얼마나 빠른지를 비교해 보기 위해서 $O(N^2)$ 알고리즘을 구현해 봅시다. $O(N^2)$ 알고리즘은 고등학교 수학책에 등장하는 방법을 그대로 구현한 것입니다. 최고차항부터 하나씩 보면서, 몫의 최고차항을 결정하고, 나누는 다항식과 곱해서 원래 다항식에서 빼는 것을 반복하는 것이죠. 예를 들어, $2x^4 - 3x^3 + 2x^2 - x + 1$을 $x^2 - x - 1$로 나누는 것은 아래처럼 계산할 수 있습니다.

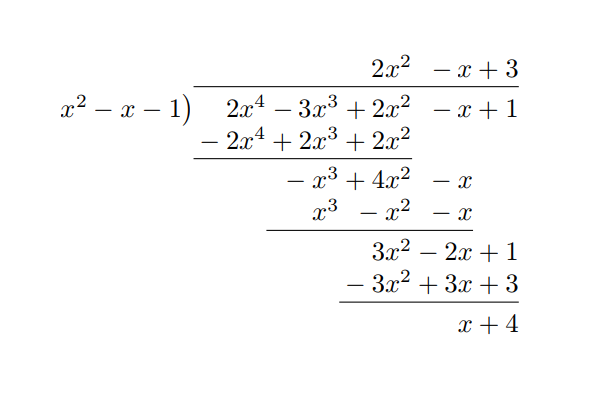
이 알고리즘을 코드로 구현하면 아래와 같습니다.

#include <iostream>
#include <vector>

using namespace std;

typedef vector<double> poly;

poly divide_n2(poly a, poly b) {
	poly q;
	for (int i = 0; i + b.size() <= a.size(); i++) {
		q.push_back(a[i] / b[0]);
		for (int j = 0; j < b.size(); j++) a[i + j] -= q[i] * b[j];
	}
	return q;
}

int main() {
	poly a, b, q;
	int n, m;

	cin >> n;
	a.resize(n);
	for (int i = 0; i < n; i++) cin >> a[i];
	cin >> m;
	b.resize(m);
	for (int i = 0; i < m; i++) cin >> b[i];

	q = divide_n2(a, b);

	for (int i = 0; i < q.size(); i++) cout << q[i] << ' ';
	cout << endl;

	return 0;
}

빠른 다항식 나눗셈

편의상, 앞으로 $x$에 대한 $N$차 다항식 $A(x)$를 $x$에 대한 $M$차 다항식 $B(x)$로 나눈다고 하겠습니다. 이 때, $N$은 $M$ 이상입니다. 또한, 나눗셈의 몫을 $Q(x)$, 나눗셈의 나머지를 $R(x)$라고 하겠습니다. 그러면 $Q(x)$는 $x$에 대한 $N-M$차 다항식이 되고, $R(x)$는 $x$에 대한 $M-1$차 다항식이 됩니다.

위에서 예시로 든 다항식 나눗셈의 경우, $N = 4$, $M = 2$이고, $A(x) = 2x^4 - 3x^3 + 2x^2 - x + 1$, $B(x) = x^2 - x - 1$, $Q(x) = 2x^2 - x + 3$, $R(x) = x + 4$가 됩니다. 앞으로의 과정들을 이 예시와 함께 설명할 것입니다.

먼저, 나눗셈 정리에 의해 다음이 성립합니다.

$ \begin{align} A(x) & = B(x) Q(x) + R(x) \ 2x^4 - 3x^3 + 2x^2 - x + 1 & = (x^2 - x - 1)(2x^2 - x + 3) + (x + 4) \end{align} $

$x$에 $z^{-1}$을 대입하고, 양변에 $z^N$을 곱해 정리하면 다음처럼 됩니다.

$ \begin{align} z^N A(z^{-1}) & = (z^M B(z^{-1})) (z^{N-M} Q(z^{-1})) + z^{N-M+1} (z^{M-1} R(z^{-1})) \ z^4 - z^3 + 2z^2 - 3z + 2 & = (-z^2 - z + 1)(3z^2 - z + 2) + z^3 (4z + 1) \end{align} $

여기서, $z^N A(z^{-1})$, $z^M B(z^{-1})$, $z^{N-M} Q(z^{-1})$, $z^{M-1} R(z^{-1})$는 $A(x)$, $B(x)$, $Q(x)$, $R(x)$의 계수 순서를 바꾸고 $x$를 $z$로 바꾼 것임을 알 수 있습니다. 이들을 $A’(z)$, $B’(z)$, $Q’(z)$, $R’(z)$라고 하고 식을 다시 적으면 다음과 같습니다.

$A’(z) = B’(z) Q’(z) + z^{N-M+1} R’(z)$

양변을 $z^{N-M+1}$으로 나눈 나머지를 취하면 다음처럼 됩니다.

$ \begin{align} A’(z) & \equiv B’(z) Q’(z) & \pmod{z^{N-M+1}} \ z^4 - z^3 + 2z^2 - 3z + 2 & \equiv (-z^2 - z + 1)(3z^2 - z + 2) & \pmod{z^3} \end{align} $

만약, 어떤 다항식 $B’^{-1}(z)$가 존재해서, $B’(z) B’^{-1}(z) \equiv 1 \pmod{z^{N-M+1}}$을 만족한다면, 양변에 $B’^{-1}(z)$를 곱해서 다음을 얻습니다.

$ A’(z) B’^{-1}(z) \equiv B’(z) B’^{-1}(z) Q’(z) \equiv Q’(z) \pmod{z^{N-M+1}} $

예시의 경우에는 $(-z^2 - z + 1)(2z^2 + z + 1) \equiv 1 \pmod{z^3}$이므로, 다음을 확인할 수 있습니다.

$ (z^4 - z^3 + 2z^2 - 3z + 2)(2z^2 + z + 1) \equiv 3z^2 - z + 2 \pmod{z^3} $

여기서, $Q’(z)$는 $z$에 대한 $N-M$차 다항식임에 주목해 주십시오. $B’^{-1}(z)$를 빠르게 계산할 수 있다면, $A’(z)$와 $B’^{-1}(z)$를 곱하고 $z^{N-M}$ 이하인 항만 남기는 것으로 $Q’(z)$를 구할 수 있습니다. $Q’(z)$의 계수 순서를 바꾸면, $Q(x)$의 계수를 얻을 수 있으므로 $B’^{-1}(z)$가 존재하고 빠르게 계산할 수 있다면 다항식 나눗셈을 빠르게 할 수 있게 됩니다.

$B’^{-1}(z)$

그렇다면 $B’^{-1}(z)$는 항상 존재할까요? 존재한다면 어떻게 빠르게 구할 수 있을까요? 결론부터 말하자면 항상 존재하고 다항식의 곱셈만큼 빠르게 계산할 수 있습니다. 이제 그 방법을 소개합니다.

먼저, $B’(z)B’^{-1}(z) \equiv 1 \pmod z$를 만족하는 $B’^{-1}(z)$를 구해봅시다. $B’(z)$의 상수항을 $c$라고 하면, $B’^{-1}(z) = c^{-1}$이 됩니다. 예시의 경우에는 상수항이 $1$이므로 $1$이 됩니다.

이제, $B’(z)U(z) \equiv 1 \pmod{z^K}$를 만족하는 $K-1$차 다항식 $U(z)$를 알고 있다는 가정 하에, $B’(z)V(z) \equiv 1 \pmod{z^{2K}}$를 만족하는 $2K-1$차 다항식 $V(z)$를 구할 것입니다. 여기서 $V(z)$는 어떤 $K-1$차 다항식 $T(z)$에 대해 다음과 같은 꼴이 됩니다.

$ \begin{align} V(z) & = U(z) + T(z) z^K \ z + 1 & = 1 + (1) z^1 \end{align} $

$B’(z)$를 $k-1$차 다항식 $B’_0(z)$와 $M-K$차 다항식 $B’_1(z)$에 대해 $B’(z) = B’_0(z) + B’_1(z) z^K$라고 합시다. 또한, $B’_0(z) U(z) = 1 + W(z) z^K$라고 하면 다음을 얻습니다.

$ B’(z) V(z) = (B’_0(z) + B’_1(z) z^K)(U(z) + T(z) z^K) \equiv 1 + (W(z) + B’_0(z) T(z) + B’_1(z) U(z)) z^K \pmod{z^{2K}} $

$B’(z)V(z) \equiv 1 \pmod {z^{2K}}$이므로,

$ W(z) + B’_0(z) T(z) + B’_1(z) U(z) \equiv 0 \pmod {z^K} $

양변에 $U(z)$를 곱하고 $B’_0(z) U(z) \equiv 1 \pmod {z^K}$임을 이용하면 다음을 얻습니다.

$ W(z) U(z) + T(z) + B’_1(z) U^2(z) \equiv 0 \pmod {z^k} $

$ T(z) \equiv -U(z) (W(z) + B’_1(z) U(z)) \pmod {z^k} $

얻은 결과를 가지고 $V(z)$를 다시 한 번 정리해 보면,

$ \begin{align} V(z) & \equiv U(z)(1 - W(z) z^K + B’_1(z) U(z) z^K) \ & \equiv U(z)(2 - B’_0(z) U(z) - B’_1(z) U(z) z^K) \ & \equiv U(z)(2 - B’(z) U(z)) \pmod{z^{2K}} \ z + 1 & \equiv (1) ( 2 - (-z^2 - z + 1) (1)) \pmod{z^2} \end{align} $

위 계산식을 여러 번 적용해서, 차수가 $N-M$ 이상이 될 때까지 반복하면 $B’^{-1}(z)$를 구할 수 있습니다.

$ (z + 1)(2 - (-z^2 - z + 1)(z + 1)) \equiv 2z^2 + z + 1 \pmod{z^3} $

$O(N \log N)$ 알고리즘

지금까지 소개한 것을 종합하면, 다항식의 나눗셈을 다항식의 덧셈, 뺄셈, 곱셈만으로 구할 수가 있다는 것입니다. 들어가며에서 빠른 푸리에 변환을 이용하면 $O(N \log N)$의 시간복잡도로 곱셈을 할 수 있다고 했는데, 이 방법을 적용하면 $O(N \log N)$의 시간에 다항식 나눗셈을 할 수가 있습니다. 아래는 이를 구현한 코드입니다.

#include <iostream>
#include <vector>
#include <complex>
#include <cmath>

using namespace std;

typedef vector<double> poly;
typedef complex<double> cd;

void FFT(vector<cd> &a, bool inv) {
	int n = a.size();
	for (int i = 1, j = 0; i < n; i++) {
		for (int k = n / 2; (j ^= k) < k; k /= 2);
		if (i < j) swap(a[i], a[j]);
	}
	for (int i = 1; i < n; i *= 2) {
		double w = acos(-1) / i;
		if (inv) w = -w;
		cd x(cos(w), sin(w));
		for (int j = 0; j < n; j += i * 2) {
			cd y(1);
			for (int k = 0; k < i; k++) {
				cd z = a[i + j + k] * y;
				a[i + j + k] = a[j + k] - z;
				a[j + k] += z;
				y *= x;
			}
		}
	}
	if (inv) for (int i = 0; i < n; i++) a[i] /= n;
}

poly multiply(poly a, poly b) {
	int n;
	for (n = 1; n < a.size() + b.size(); n *= 2);
	vector<cd> A(n), B(n);
	for (int i = 0; i < a.size(); i++) A[i] = a[i];
	for (int i = 0; i < b.size(); i++) B[i] = b[i];
	FFT(A, false);
	FFT(B, false);
	for (int i = 0; i < n; i++) A[i] *= B[i];
	FFT(A, true);
	poly r(a.size() + b.size());
	for (int i = 0; i < r.size(); i++) r[i] = A[i].real();
	return r;
}

poly inverse(poly a, int m) {
	poly r(1);
	r[0] = 1 / a[0];
	for (int n = 1; n < m;) {
		n = min(n * 2, m);
		poly t(a.begin(), n < a.size() ? a.begin() + n : a.end());
		t = multiply(r, t);
		t.resize(n);
		t[0] = 2 - t[0];
		for (int i = 1; i < n; i++) t[i] = -t[i];
		r = multiply(r, t);
		r.resize(n);
	}
	return r;
}

poly divide_nlogn(poly a, poly b) {
	int m = a.size() - b.size() + 1;
	poly q = multiply(a, inverse(b, m));
	q.resize(m);
	return q;
}

int main() {
	poly a, b, q;
	int n, m;

	cin >> n;
	a.resize(n);
	for (int i = 0; i < n; i++) cin >> a[i];
	cin >> m;
	b.resize(m);
	for (int i = 0; i < m; i++) cin >> b[i];

	q = divide_nlogn(a, b);

	for (int i = 0; i < q.size(); i++) cout << q[i] << ' ';
	cout << endl;

	return 0;
}

여기서 FFT와 multiply 함수는 다항식 곱셈을 해 주는 함수로, 다른 더 빠른 다항식 곱셈 구현체로 바꿔도 무방합니다.

성능 비교

이렇게 구현한 $O(N \log N)$ 다항식 나눗셈은 얼마나 더 빠를까요? 성능을 비교해 보기 위해서 아래와 같은 벤치마크 코드를 작성해서 실행해 보았습니다.

#include <iostream>
#include <vector>
#include <random>
#include <sys/time.h>

using namespace std;

typedef vector<double> poly;

const double RNG = 0.1, EPS = 10;
const int TC = 10, N = 200000, M = 100000;

poly generate(int n) {
	static random_device rd;
	static uniform_real_distribution<double> urd(-RNG, RNG);
	poly a(n);
	for (int i = 0; i < n; i++) a[i] = urd(rd);
	return a;
}

pair<poly, poly> in[TC];
poly out[TC], ans[TC];

void generate_tc() {
	for (int t = 0; t < TC; t++) {
		poly b = generate(M + 1), q = generate(N - M + 1), r = generate(M);
		poly a(N + 1);
		if (b[0] < 0) b[0] -= EPS;
		else b[0] += EPS;
		for (int i = 0; i <= M; i++) for (int j = 0; j <= N - M; j++) a[i + j] += b[i] * q[j];
		for (int i = 0; i < M; i++) a[N - i] += r[M - i - 1];
		in[t].first = a;
		in[t].second = b;
		ans[t] = q;
	}
}

void report_result() {
	double me = 0;
	for (int t = 0; t < TC; t++) {
		for (int i = 0; i <= N - M; i++) {
			double e = abs(out[t][i] - ans[t][i]);
			if (e > me) me = e;
		}
	}
	cout << "maximum absolute error: " << me << endl;
}

double get_time() {
	struct timeval tv;
	gettimeofday(&tv, NULL);
	return tv.tv_sec + tv.tv_usec / 1000000.;
}

poly divide_n2(poly, poly);
poly divide_nlogn(poly, poly);

int main() {
	double st, en;

	cout << "N = " << N << ", M = " << M << ", TC = " << TC << endl;
	cout << "RNG = " << RNG << ", EPS = " << EPS << endl;
	cout << "Generating testcases..." << endl;
	generate_tc();

	cout << "Running divide_n2..." << endl;
	st = get_time();
	for (int t = 0; t < TC; t++) out[t] = divide_n2(in[t].first, in[t].second);
	en = get_time();
	cout << "running time: " << (en - st) / TC << endl;
	report_result();

	cout << "Running divide_nlogn..." << endl;
	st = get_time();
	for (int t = 0; t < TC; t++) out[t] = divide_nlogn(in[t].first, in[t].second);
	en = get_time();
	cout << "running time: " << (en - st) / TC << endl;
	report_result();
}

아래는 N = 100000, M = 50000, TC = 10일 때의 실행 결과입니다.

N = 100000, M = 50000, TC = 10
RNG = 0.1, EPS = 10
Generating testcases...
Running divide_n2...
running time: 2.85076
maximum absolute error: 6.1607e-14
Running divide_nlogn...
running time: 0.352411
maximum absolute error: 1.27981e-09

10만 정도에서도 약 8배 가량 성능 차이가 납니다. N이 더 커지면 어떨까요?

N = 200000, M = 100000, TC = 10
RNG = 0.1, EPS = 10
Generating testcases...
Running divide_n2...
running time: 12.7683
maximum absolute error: 1.07481e-11
Running divide_nlogn...
running time: 0.771939
maximum absolute error: 4.89914e-06

20만애서는 16.5배 정도 차이가 납니다.

마치며

빠른 다항식 곱셈 알고리즘을 이용하여 빠른 다항식 나눗셈을 하는 방법을 소개했습니다. 곱셈에 비하면 나눗셈은 사용되는 범위가 넓지는 않지만, 나눗셈 또한 곱셈만큼 빠르게 계산할 수 있으며 N이 조금만 커지더라도 $O(N^2)$ 알고리즘에 비해 성능 차이가 크다는 것을 확인할 수 있었습니다.

빠른 다항식 나눗셈

들어가며

$O(N^2)$ 알고리즘

빠른 다항식 나눗셈

$B’^{-1}(z)$

$O(N \log N)$ 알고리즘

성능 비교

마치며

특별한 정렬 알고리즘들

Web Worker-Postable 라이브러리 작성기