Delaunay Triangulation 구현
목차
개요

이 포스트를 작성하게 된 계기
이 글을 쓰게 된 계기는 학부 과정에 수학과 과목을 몰래 훔쳐 들으려고 하던 중, 계산 기하학에 대해 공부하는 과목을 알게 되었다. 바로 혹해서 들었다가 후반부에 너무 어렵고 추상적인 수학 파트가 나와서 좌절했다가, 초반부의 Deluanay Triangulation 만큼은 흥미롭고 응용 분야가 넓어서 공유하면 좋겠다 싶어서 가져오게 되었다.
간단한 설명
Deluanay Triangulation, 한국어로 들로네 삼각분할은 간단히 말하면 2차원 평면에 분포하는 점들을 대상으로 삼각형들을 만드는데 각각의 삼각형들은 본인들 세 점을 제외한 다른 점을 포함하지 않게끔 삼각형을 만들어 분할하는 것을 의미한다. 이러한 특징 때문에 특정 점에서 가장 가까운 점을 찾는데 도움을 주거나 할 수 있다. 이제 자세한 내용을 들여다 보도록 하자.
원리
알고리즘
우선 알고리즘의 원리는 다음과 같다.
먼저 거대한 삼각형을 그린다.
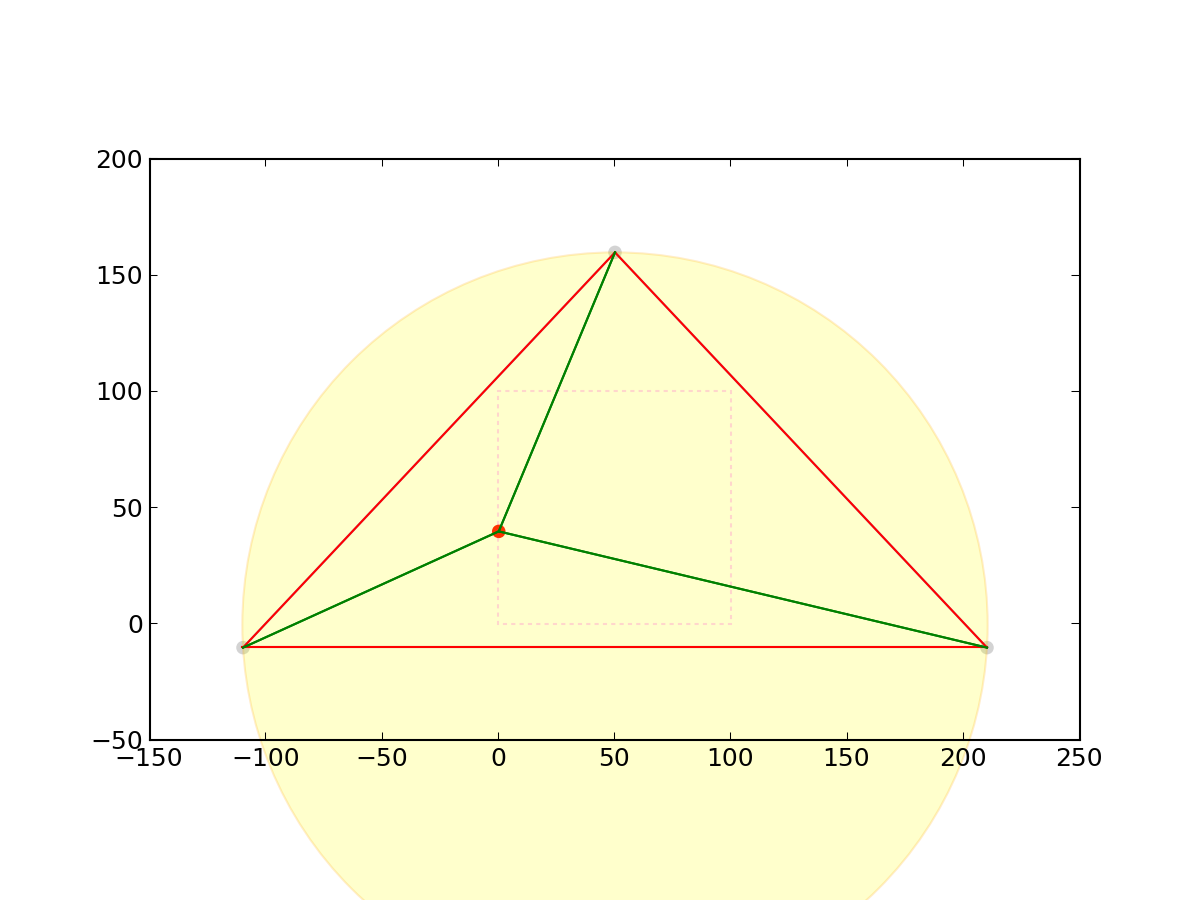
이러한 거대한 삼각형을 Super Triangle 이라고 한다.
그 다음, 입력받은 좌표를 순서대로 좌표평면에 넣어가면서 Triangulation을 진행하는데 규칙은 다음과 같다.
- 외접원 안에 들어오는 삼각형들은 Bad Triangle 이라고 하는데 이 Bad Triangle 끼리 짝수번 접하는 변은 전부 제거한다.
- 그렇게 나온 Polygon의 변과 추가된 좌표를 이어서 새로운 삼각형들을 만들어준다.
- Bad Triangle들은 전부 제거한다.
- 1로 돌아가 그 모든 과정을 반복한다.
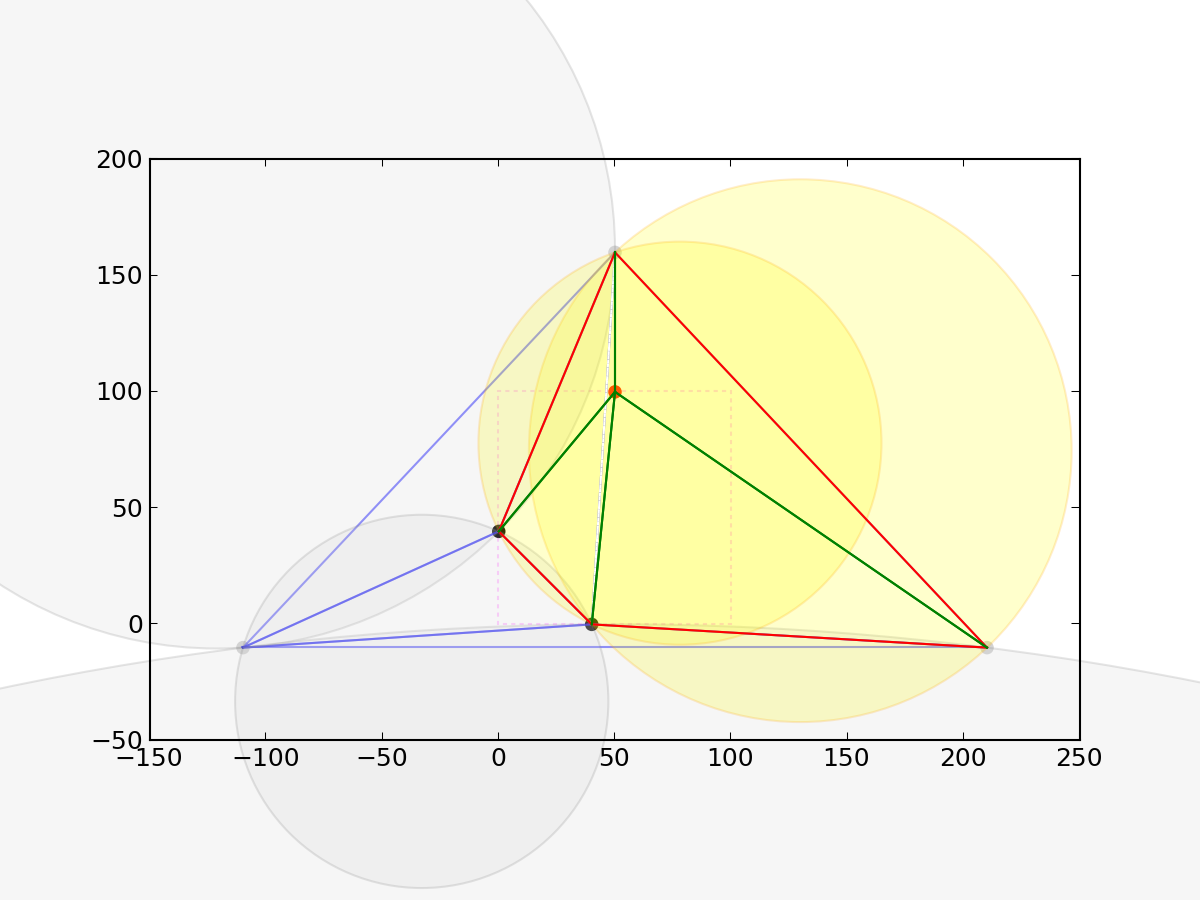
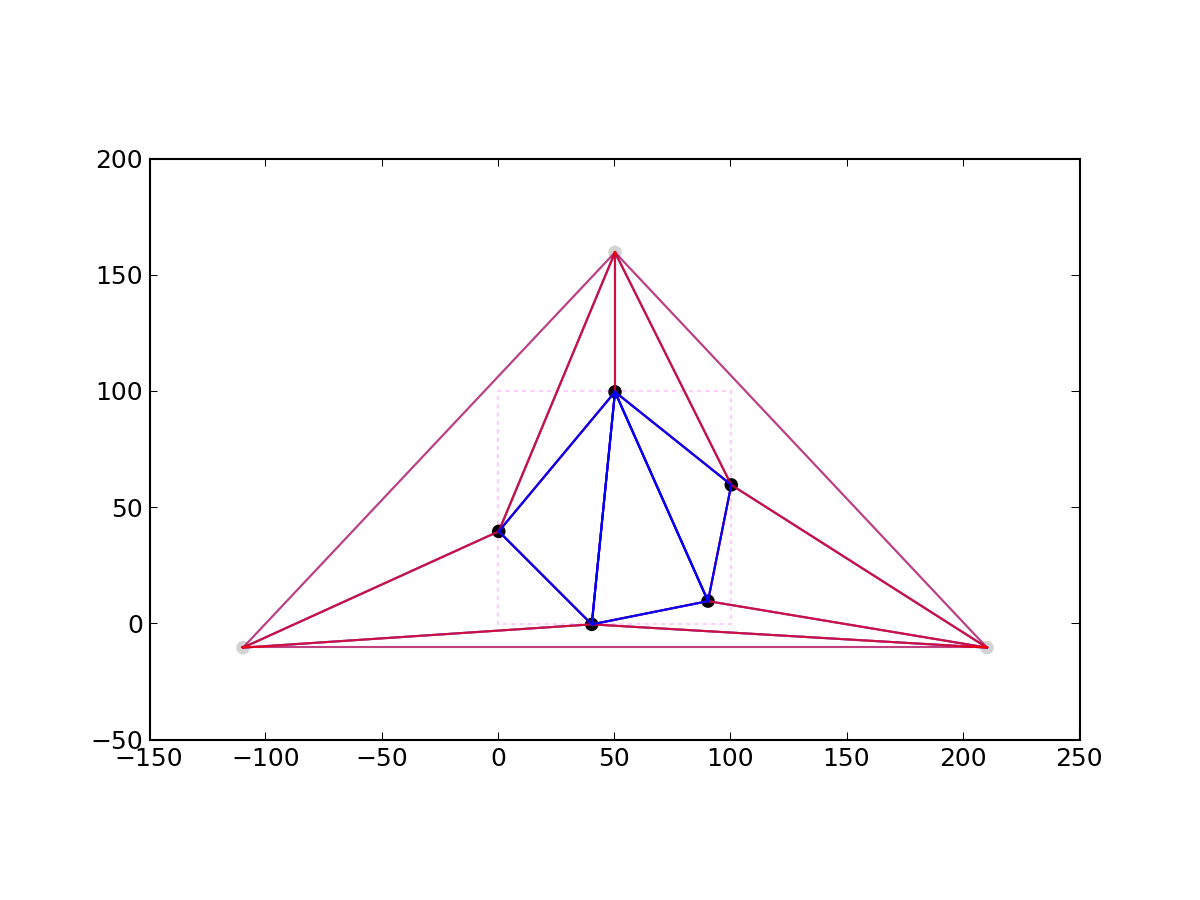
시간복잡도는 최악의 경우 $O(N^2)$ 의 시간복잡도를 가진다. 생각해보면 원리는 간단하다. i번째 좌표가 추가될 때 $O(i)$ 개의 삼각형이 추가될 수 있기 때문이다. 이것은 1부터 N까지의 합과 같고, 결국엔 $O(N^2)$ 의 시간복잡도를 가지게 되는것이다.
아래는 pseudo code 이다.
v_list = list of vertexes
triagle_list = [super_triangle]
for v in v_list
badTriangle = []
polygon = []
for triangle in triangle_list
if v in circumcirlce of triangle
insert triangle into badTriangle
insert edge of badTriangle into polygon
delete edge of polygon when same edge exists twice
for edge in polygon
make triangle use v and edge
insert triangle into triangle_list
delete badTriangle from polygon
delete super_triangle from triangle_list
추가적으로 필요한 지식
이때 몇가지 궁금할 것이 있을것이다. 하나는 Circumcircle 인데, 외접원을 뜻하는 뜻으로 외접원 안에 v가 들어가면 그 삼각형을 Bad Triangle 취급을 하는 것이다. 이때 삼각형의 외접원안에 v가 들어오는것을 확인하기 위해서는 다음과 같은 식이 필요하다.
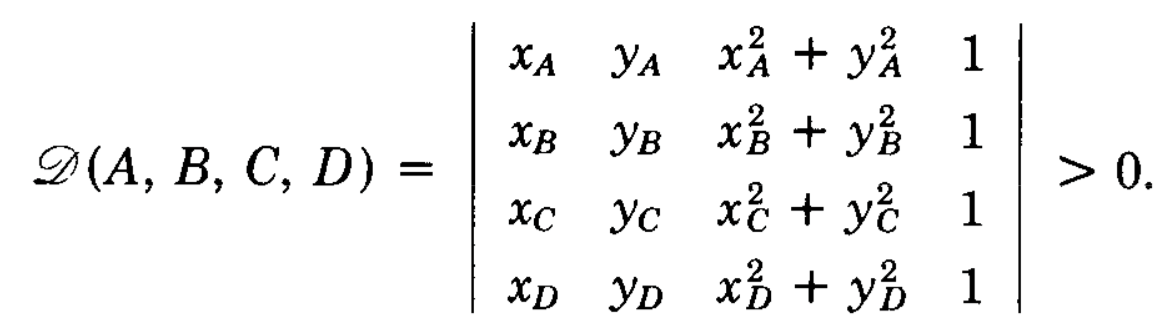
원리는 $(x, y) -> (x, y, x^2 + y^2)$ 으로 2차원 평면 상의 좌표를 3차원 곡면 상의 좌표로 옮긴다고 해보자. 이때 삼각형의 세 좌표가 이루는 2차원 plane 보다 위에 있다면 determinant 가 양수, 아래에 있다면 음수, 정확히 같은 평면상에 위치한다면 0 이다.
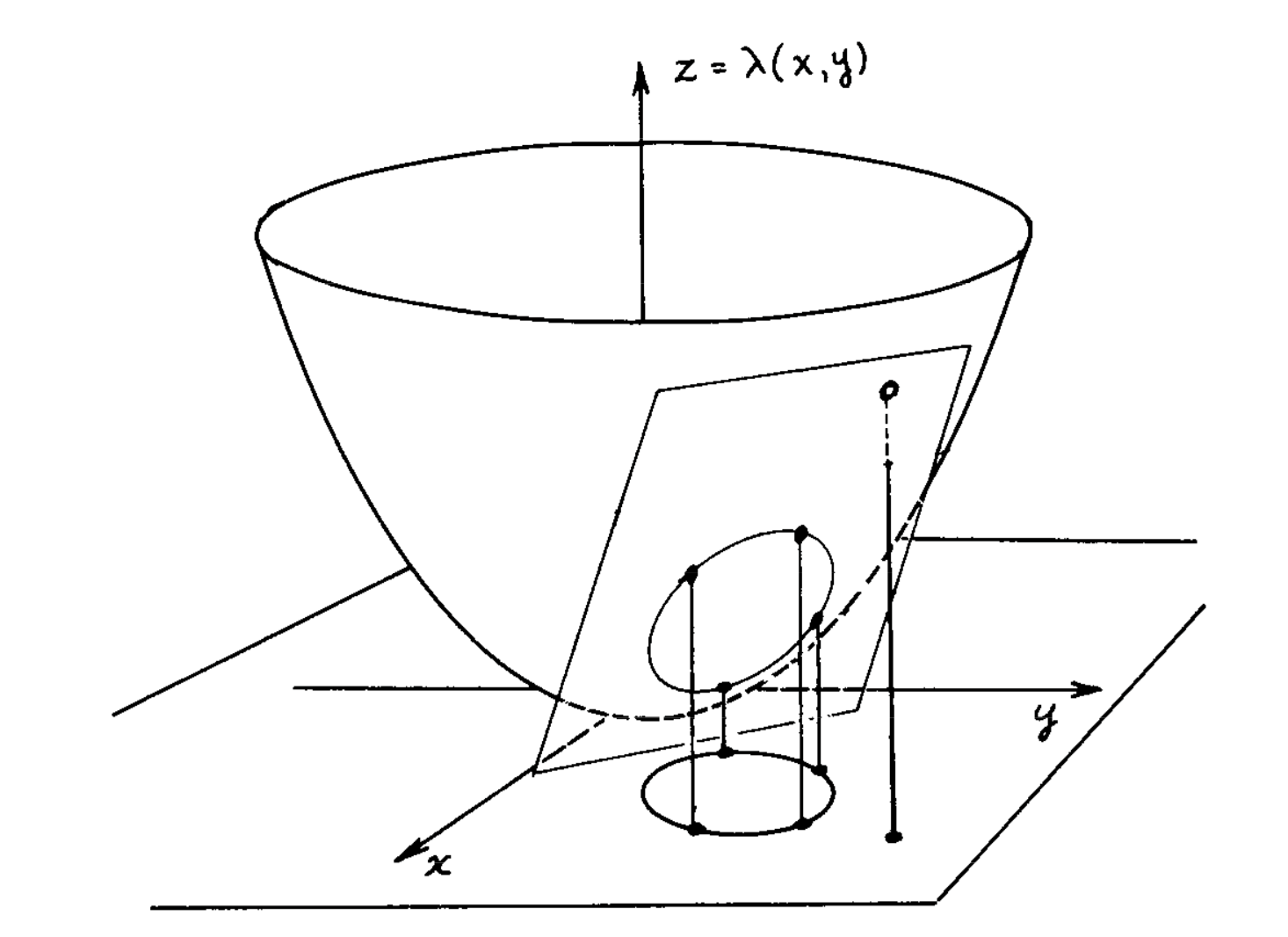
즉, CCW와 determinant를 구해주면 간단하게 판별할 수 있다. determinant와 CCW를 구하는 식은 아래 구현단계의 코드에서 확인하길 바란다.
구현
구조체
struct vect { // 벡터 구조체, 프로젝션 벡터나 코사인, 내적 외적등을 편리하게 구하기 위하여 구현
double x;
double y;
vect() { x = y = 0; }
vect(double x, double y) {
this->x = x;
this->y = y;
}
const double dist() const { // 거리
return sqrt(x * x + y * y);
}
const double inner(const vect &a) const { // 내적
return x * a.x + y * a.y;
}
const double cross(const vect &a) const { // 외적(determinant)
return x * a.y - y * a.x;
}
const vect operator+ (const vect &a) const { // 벡터의 합
return vect(x + a.x, y + a.y);
}
const vect operator- (const vect &a) const { // 벡터의 차
return vect(x - a.x, y - a.y);
}
const vect operator* (const double &a) const { // 스칼라 곱
return vect(a * x, a * y);
}
const vect proj(const vect &a) const { // projection vector
return *this * (inner(*this) / inner(a));
}
const double get_cos(const vect &a) const { // 두 벡터의 코사인
return inner(a) / (dist() * a.dist());
}
};
먼저 좌표를 구성할 좌표벡터 구조체이다. 각각 내적, 외적, 덧셈, 뺄셈, 스칼라 곱, 프로젝션 벡터, 코사인 등을 구할 수 있도록 미리 구현해놓은 좌표벡터 구조체이다.
struct edg { // edge 구조체, 말 그대로 변에 대한 구조체
int a;
int b;
edg() { a = b = 0; }
edg(int a, int b) {
if(a < b) {
this->a = a;
this->b = b;
}
else {
this->a = b;
this->b = a;
}
}
const bool operator== (const edg &x) const {
return a == x.a && b == x.b;
}
const bool operator< (const edg &x) const {
if(a == x.a) return b < x.b;
return a < x.a;
}
};
변에 대한 구조체이다. 좌표의 번호 두개를 집어넣는것으로 구현했으며 순서에 맞게끔 넣도록 하였다.
struct tri { // triangle 구조체, 말 그대로 삼각형에 대한 구조체
int a;
int b;
int c;
tri() { a = b = c = 0;}
tri(int a, int b, int c) {
this->a = a;
this->b = b;
this->c = c;
}
};
삼각형에 대한 구조체이다. 좌표의 번호 세개를 집어넣는것으로 구현했으며 순서에 맞게끔 넣도록 하였다.
외접원 안에 속하는지 판별
bool is_circum(tri cur, int i, vector<vect> &point) { // 외접원안에 점이 들어오는지 확인
double ccw = (point[cur.b] - point[cur.a]).cross(point[cur.c] - point[cur.a]);
double adx=point[cur.a].x-point[i].x, ady=point[cur.a].y-point[i].y,
bdx=point[cur.b].x-point[i].x, bdy=point[cur.b].y-point[i].y,
cdx=point[cur.c].x-point[i].x, cdy=point[cur.c].y-point[i].y,
bdxcdy = bdx * cdy, cdxbdy = cdx * bdy,
cdxady = cdx * ady, adxcdy = adx * cdy,
adxbdy = adx * bdy, bdxady = bdx * ady,
alift = adx * adx + ady * ady,
blift = bdx * bdx + bdy * bdy,
clift = cdx * cdx + cdy * cdy;
double det = alift * (bdxcdy - cdxbdy)
+ blift * (cdxady - adxcdy)
+ clift * (adxbdy - bdxady);
if(ccw > 0) return det >= 0;
else return det <= 0;
}
우선 ccw는 중심 좌표벡터를 기준으로 두 좌표벡터의 차이를 구해서 만들어진 새로운 두개의 벡터의 determinant로 구한다. 이후 아래의 determinant 식을 사용하여 구한다. 유도 방법이 상당히 복잡하여 다음 블로그를 참고하였다.
주 알고리즘
int main() {
freopen("input.txt", "rt", stdin); // input.txt 를 불러와서
freopen("output.txt", "w", stdout); // output.txt 로 triangluation 된 값을 내보낸다.
int n;
scanf("%d",&n);
vector<vect> point(n + 3); // super triangle 을 만들기 위하여 3만큼 더 크게 잡는다.
for(int i = 0; i < n; i++) {
double x, y;
scanf("%lf %lf", &x, &y);
point[i] = vect(x, y);
}
// Super Triangle Phase
point[n] = vect(-2e9, -2e9);
point[n + 1] = vect(2e9, -2e9);
point[n + 2] = vect(0, 2e9);
vector<tri> triangle;
triangle.push_back(tri(n, n + 1, n + 2));
// Delaunay Triangluation
// Time Complexity O(N^2 log N) << Polygon 구현 과정을 set으로 구현했다.
for(int i = 0; i < n; i++) {
set<edg> polygon;
vector<int> complete(triangle.size(), 0);
for(int j = 0; j < triangle.size(); j++) {
if(complete[j]) continue;
tri cur = triangle[j];
if(is_circum(cur, i, point)) {
if(polygon.count(edg(cur.a, cur.b))) polygon.erase(edg(cur.a, cur.b)); // 만약 겹치는 edge라면 제거
else polygon.insert(edg(cur.a, cur.b)); // 안 겹치면 삽입
if(polygon.count(edg(cur.b, cur.c))) polygon.erase(edg(cur.b, cur.c));
else polygon.insert(edg(cur.b, cur.c));
if(polygon.count(edg(cur.c, cur.a))) polygon.erase(edg(cur.c, cur.a));
else polygon.insert(edg(cur.c, cur.a));
swap(complete[j], complete[triangle.size() - 1]); // bad triangle 은 제거한다.
swap(triangle[j], triangle[triangle.size() - 1]);
triangle.pop_back();
j--;
continue;
}
complete[j] = true;
}
for(auto &cur : polygon) {
if((point[cur.b] - point[cur.a]).cross(point[i] - point[cur.a]) == 0) continue; // 일직선이므로 삼각형이 될 수 없다. 따라서 무시
triangle.push_back(tri(cur.a, cur.b, i));
}
}
// SuperTriangle delete
for(int i = 0; i < triangle.size(); i++) {
tri cur = triangle[i];
if(cur.a >= n || cur.b >= n || cur.c >= n) { // n ~ n+2 의 정점을 사용하는 삼각형은 모두 처분한다.
swap(triangle[i], triangle[triangle.size() - 1]);
triangle.pop_back();
i--;
continue;
}
}
printf("%d\n", triangle.size()); // triangle size 출력
for(int i = 0; i < triangle.size(); i++) {
tri cur = triangle[i];
printf("%.6lf %.6lf %.6lf %.6lf %.6lf %.6lf\n", point[cur.a].x, point[cur.a].y, point[cur.b].x, point[cur.b].y, point[cur.c].x, point[cur.c].y); // 한줄에 삼각형 하나씩 출력한다. (소수점 6째자리 까지 허용)
}
return 0;
}
주석으로 설명을 대체하도록 한다.
마무리
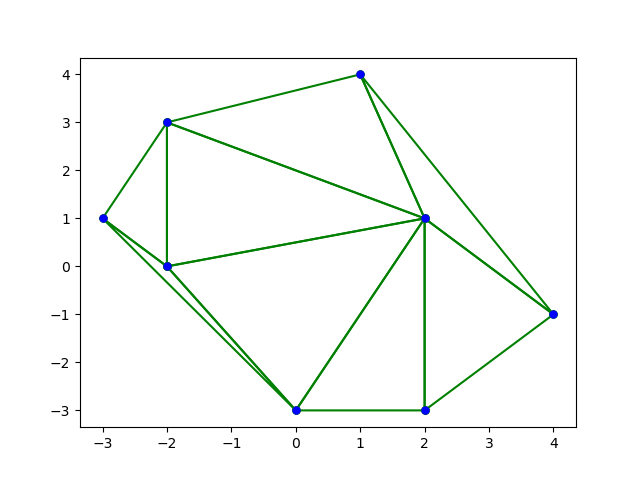
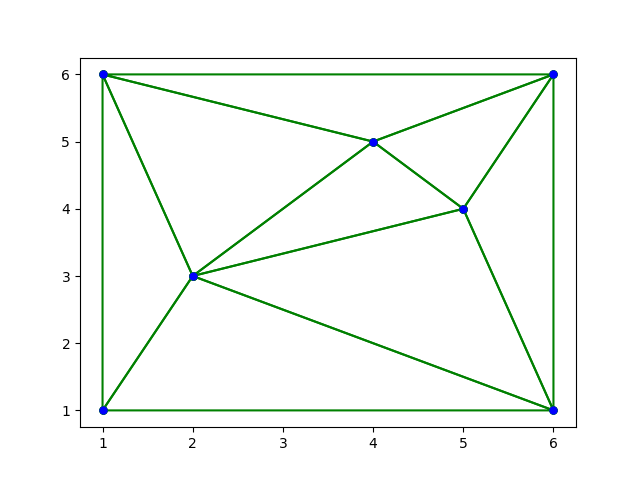
위 코드를 사용하여 추출한 데이터를 파이썬의 pyplot으로 그린 그래프들이다. 이번 블로그 포스트를 통하여 Deluanay Triangulation 에 대한 개괄적인 이해도와 앞으로 진행할 간단한 응용등에 도움이 되었으면 좋겠다. 이제 방학도 본격적으로 시작되었으니 $O(N log N)$의 시간복잡도로 구축하는 방법과 그 이외에 다양한 응용 및 PS에 적용하는것을 한번 연구해보고 싶다.
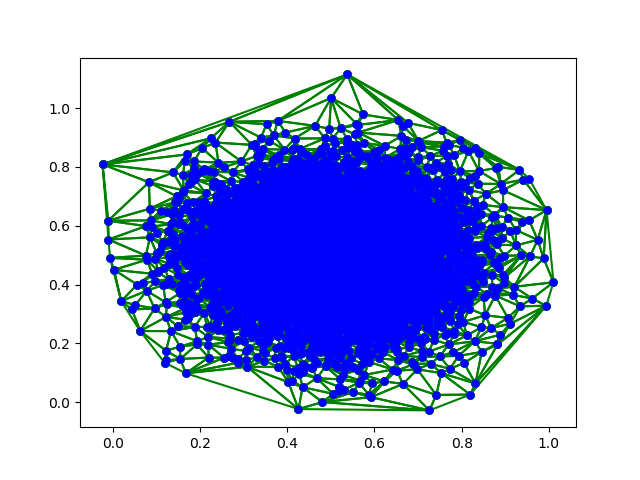
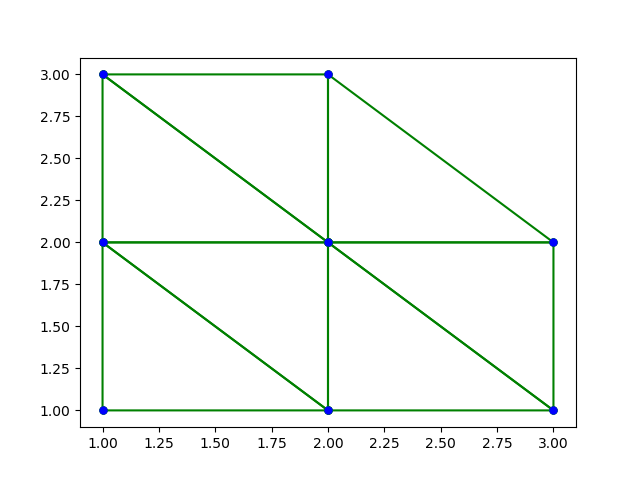
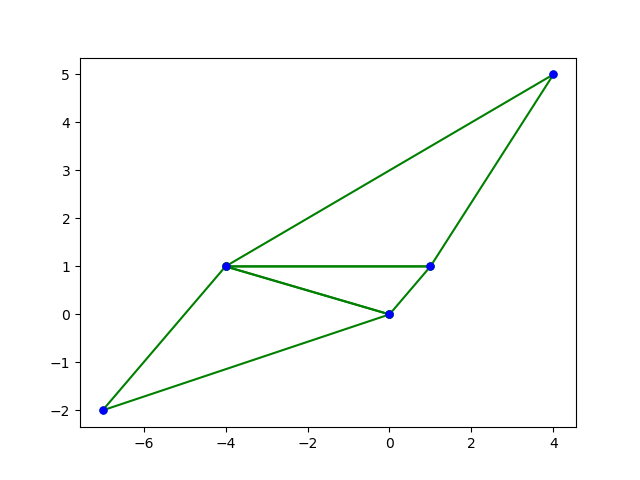
참고자료
- “Primitives for the manipulation of general subdivisions and the computation of Voronoi”, ACM Transactions on Graphics, 1985, pp.74–123
- Liu, Yuanxin, and Jack Snoeyink. “A comparison of five implementations of 3D Delaunay tessellation.” Combinatorial and Computational Geometry 52 (2005): pp.439-458
- kipl.tistory.com; 삼각형 외접원의 Inclusion Test. helloktk
- en.wikipedia.org; Delaunay triangulation. Gjacquenot
- en.wikipedia.org; Bowyer Watson algorithm. Johann Dreo